1-6 三维卷积

三维卷积（Convolutions over volumes）

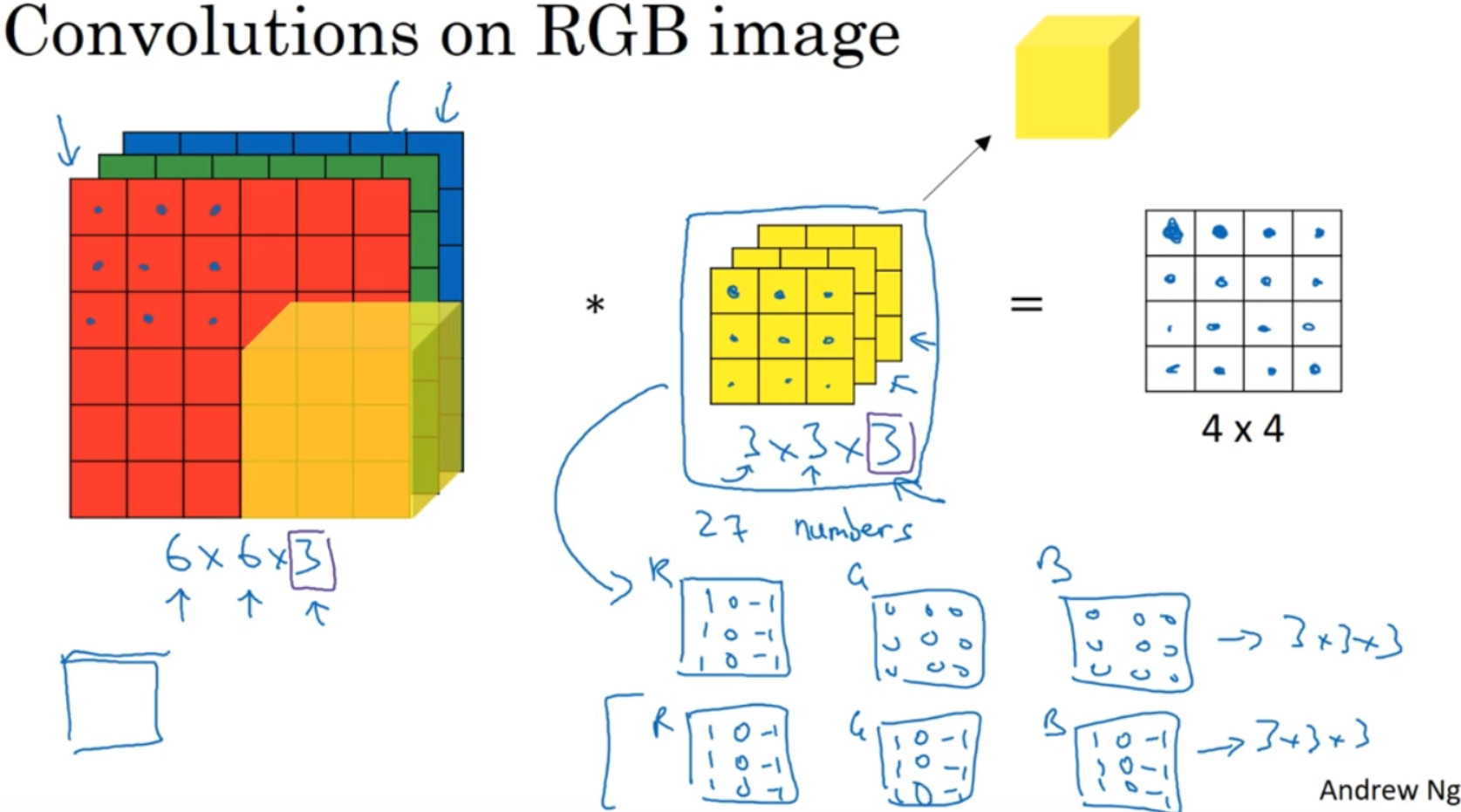
假如说你不仅想检测灰度图像的特征，也想检测 RGB 彩色图像的特征。彩色图像如果是 6×6×3，这里的 3指的是三个颜色通道，你可以把它想象成三个 6×6图像的堆叠。为了检测图像的边缘或者其他的特征，不是把它跟原来的 3×3 的过滤器做卷积，而是跟一个三维的过滤器，它的维度是 3×3×3，这样这个过滤器也有三层，对应红绿、蓝三个通道。

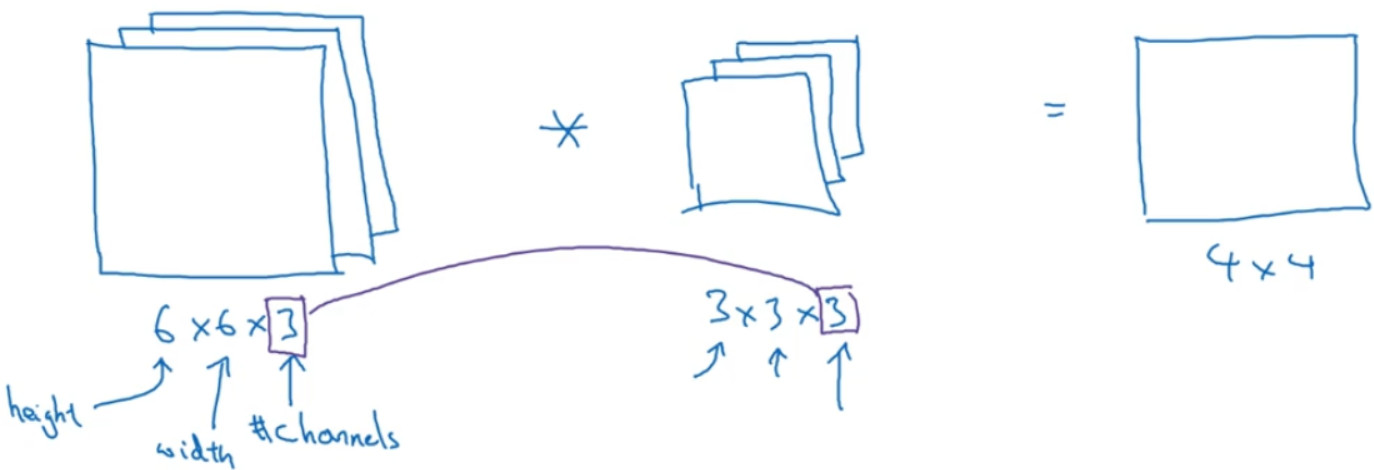
给这些起个名字（原图像），这里的第一个 6 代表图像高度，第二个 6 代表宽度，这个3 代表通道的数目。同样你的过滤器也有高，宽和通道数，并且图像的通道数必须和过滤器的通道数匹配，所以这两个数（紫色方框标记的两个数）必须相等。

这个卷积操作会是一个 4×4 的图像，注意是 4×4×1，最后一个数不是 3 了。

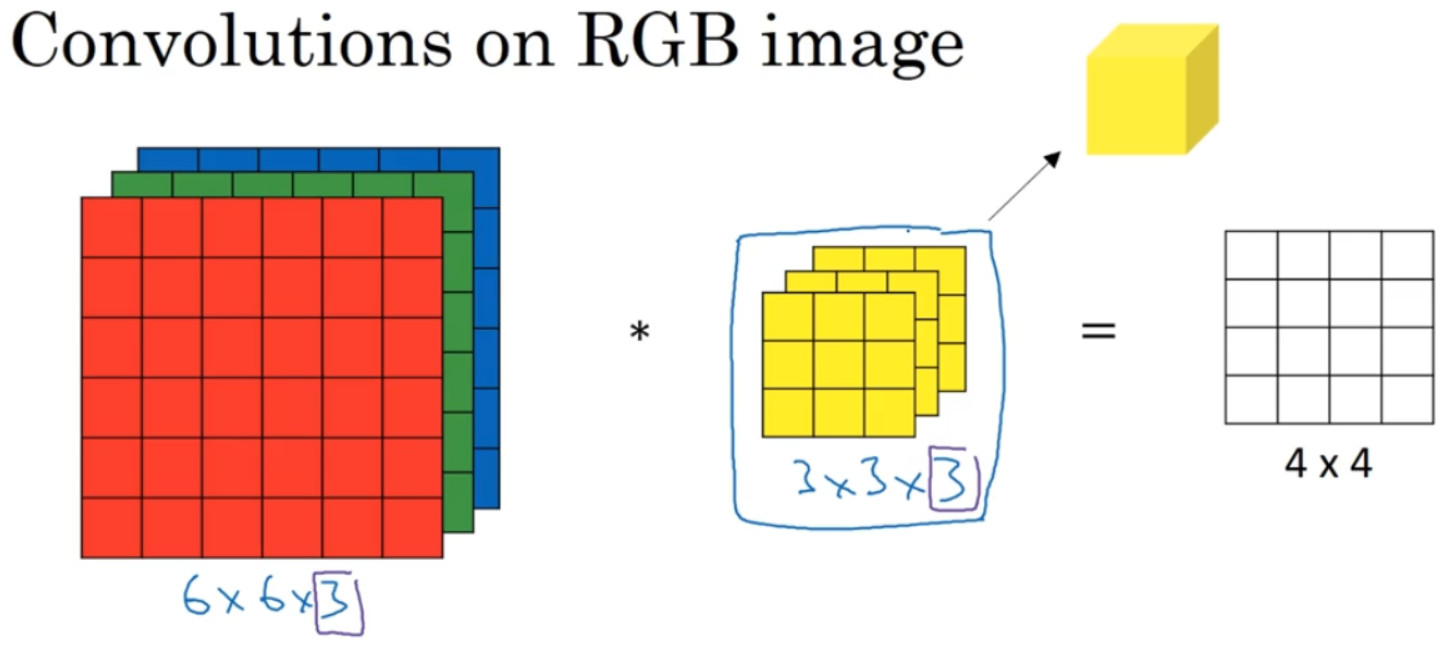
这个是 6×6×3 的图像，这个是3×3×3 的过滤器，最后一个数字通道数必须和过滤器中的通道数相匹配。为了简化这个 3×3×3过滤器的图像，我们不把它画成 3 个矩阵的堆叠，而画成这样，一个三维的立方体。

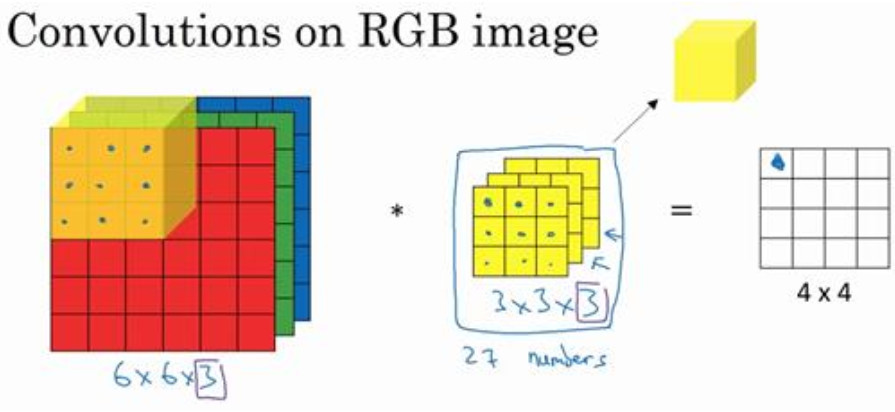
为了计算这个卷积操作的输出，你要做的就是把这个 3×3×3 的过滤器先放到最左上角的位置，这个 3×3×3 的过滤器有 27 个数， 27 个参数就是 3 的立方。依次取这 27 个数，然后乘以相应的红绿蓝通道中的数字。先取红色通道的前 9 个数字，然后是绿色通道，然后再是蓝色通道，乘以左边黄色立方体覆盖的对应的 27 个数，然后把这些数都加起来，就得到了输出的第一个数字。

如果要计算下一个输出，你把这个立方体滑动一个单位，再与这 27 个数相乘，把它们都加起来，就得到了下一个输出，以此类推。

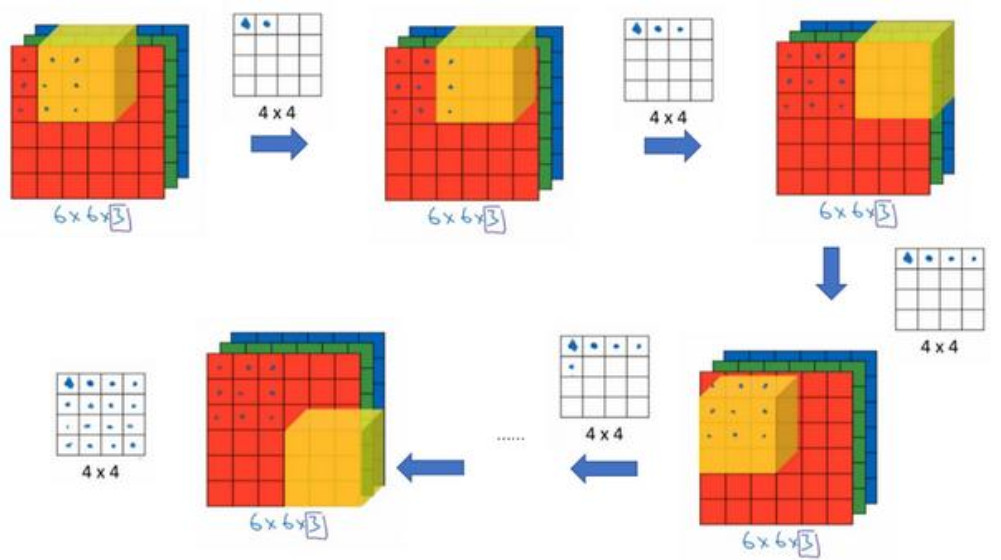
那么，这个能干什么呢？举个例子，这个过滤器是 3×3×3 的，如果你想检测图像红色通道的边缘，那么你可以将第一个过滤器设为：

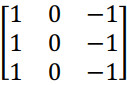
而绿色通道全为 0：

蓝色也全为 0。如果你把这三个堆叠在一起形成一个 3×3×3 的过滤器，那么这就是一个检测垂直边界的过滤器，但只对红色通道有用。或者如果你不关心垂直边界在哪个颜色通道里，那么你可以用一个这样的过滤器：

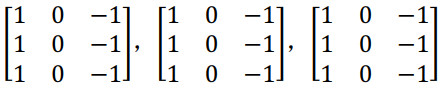
所有三个通道都是这样。所以通过设置第二个过滤器参数，你就有了一个边界检测器， 3×3×3 的边界检测器，用来检测任意颜色通道里的边界。参数的选择不同，你就可以得到不同的特征检测器，所有的都是 3×3×3 的过滤器。

按照计算机视觉的惯例，当你的输入有特定的高宽和通道数时， 你的过滤器可以有不同的高，不同的宽，但是必须一样的通道数。理论上，我们的过滤器只关注红色通道，或者只关注绿色或者蓝色通道也是可行的。

再注意一下这个卷积立方体，一个 6×6×6 的输入图像卷积上一个 3×3×3 的过滤器，得到一个 4×4 的二维输出。

如果你想同时用多个过滤器怎么办？

这个 6×6×3 的图像和这个 3×3×3 的过滤器卷积，得到 4×4 的输出。（第一个）这可能是一个垂直边界检测器或者是学习检测其他的特征。第二个过滤器可以用橘色来表示，它可以是一个水平边缘检测器。

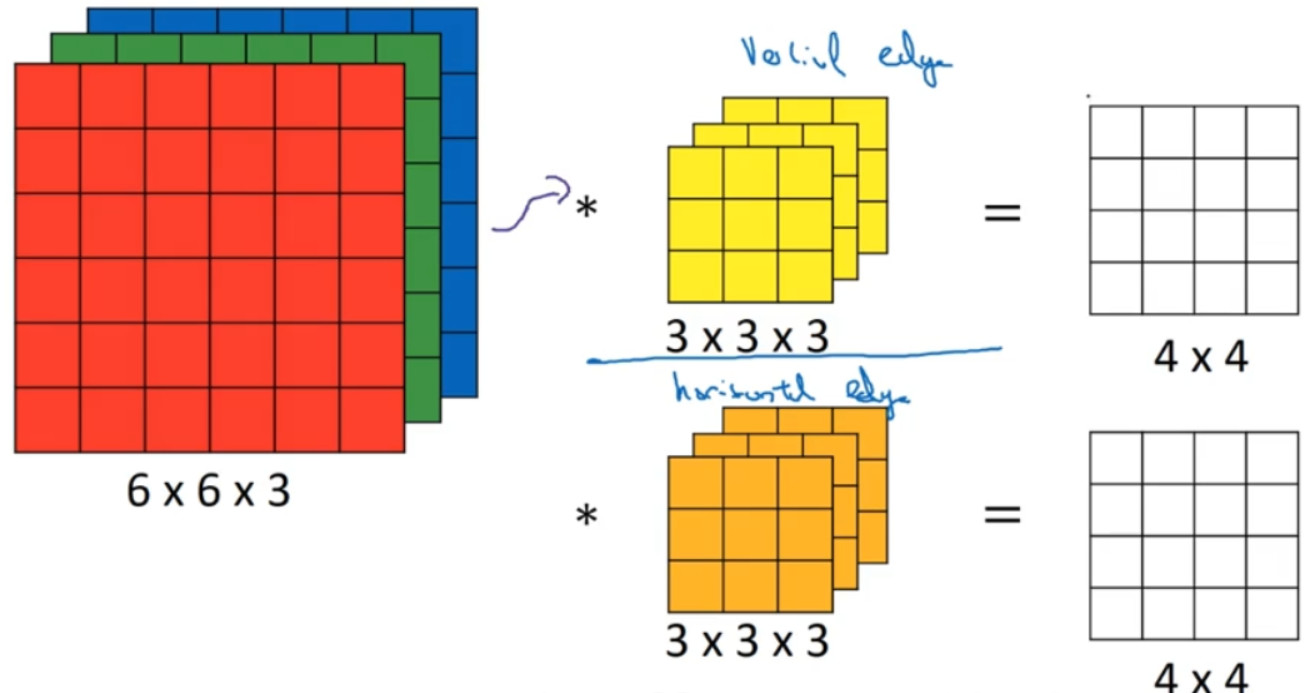
所以和第一个过滤器卷积，可以得到第一个 4×4 的输出，然后卷积第二个过滤器，得到一个不同的 4×4 的输出。我们做完卷积，然后把这两个 4×4 的输出，取第一个把它放到前面，然后取第二个过滤器输出，所以把这两个输出堆叠在一起，这样你就都得到了一个 4×4×2 的输出立方体。它用 6×6×3 的图像，然后卷积上这两个不同的 3×3 的过滤器，得到两个 4×4 的输出，它们堆叠在一起，形成一个 4×4×2 的立方体，这里的 2 的来源于我们用了两个不同的过滤器。

如果你有一个$n*n*{n_c}$（通道数）的输入图像，在这个例子中就是 6×6×3，这里的${n_c}$就是通道数目，然后卷积上一个$f*f*{n_c}$，这个例子中是 3×3×3，然后你就得到了$(n - f + 1) \times (n - f + 1) \times {n_{{c^'}}}$:

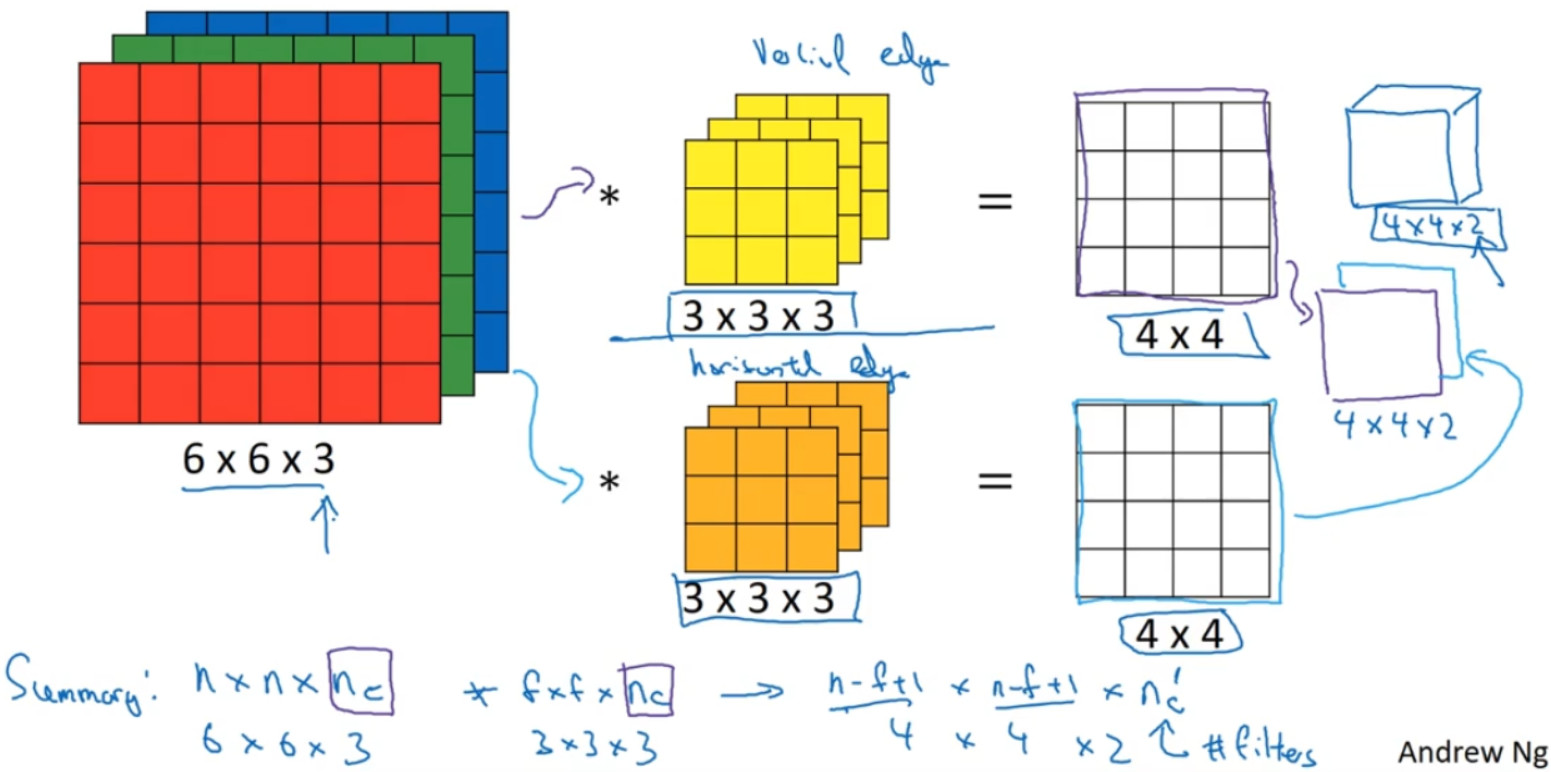
这里${n_{{c^'}}}$其实就是下一层的通道数，它就是你用的过滤器的个数，在我们的例子中，那就是 4×4×2。这个假设时用的步幅为 1，并且没有 padding。如果你用了不同的步幅或者 padding，那么这个n − f + 1数值会变化。

这个对立方体卷积的概念真的很有用，你现在可以用它的一小部分直接在三个通道的RGB 图像上进行操作。更重要的是，你可以检测两个特征，比如垂直和水平边缘或者 10 个或者 128 个或者几百个不同的特征，并且输出的通道数会等于你要检测的特征数。