1-2 单一数字评估指标

单一数字评估指标（ Single number evaluation metric）

无论你是调整超参数，或者是尝试不同的学习算法，或者在搭建机器学习系统时尝试不同手段，你会发现，如果你有一个单实数评估指标，你的进展会快得多，它可以快速告诉你，新尝试的手段比之前的手段好还是差。

我们来看一个例子，你之前听过我说过，应用机器学习是一个非常经验性的过程，我们通常有一个想法，编程序，跑实验，看看效果如何，然后使用这些实验结果来改善你的想法，然后继续走这个循环，不断改进你的算法。

比如说对于你的猫分类器，之前你搭建了某个分类器A，通过改变超参数，还有改变训练集等手段，你现在训练出来了一个新的分类器B，所以评估你的分类器的一个合理方式是观察它的查准率（precision）和查全率（recall）。

查准率的定义是在你的分类器标记为猫的例子中，有多少真的是猫。所以如果分类器A有95%的查准率，这意味着你的分类器说这图有猫的时候，有 95%的机会真的是猫。

查全率就是，对于所有真猫的图片，你的分类器正确识别出了多少百分比。实际为猫的图片中，有多少被系统识别出来。如果分类器A查全率是 90%，这意味着对于所有的图像，比如说你的开发集都是真的猫图，分类器A准确地分辨出了其中的 90%。

事实证明，查准率和查全率之间往往需要折衷，两个指标都要顾及到。你希望得到的效果是，当你的分类器说某个东西是猫的时候，有很大的机会它真的是一只猫，但对于所有是猫的图片，你也希望系统能够将大部分分类为猫，所以用查准率和查全率来评估分类器是比较合理的。

但使用查准率和查全率作为评估指标的时候，有个问题，如果分类器A在查全率上表现更好，分类器B在查准率上表现更好，你就无法判断哪个分类器更好。你需要找到一个新的评估指标，能够结合查准率和查全率。

在机器学习文献中，结合查准率和查全率的标准方法是所谓的${F_1}$分数，这个函数叫做查准率P和查全率R的调和平均数。

${F_1} = \frac{2}{{\frac{1}{P} + \frac{1}{R}}}$

在这个例子中，你可以马上看出，分类器A的${F_1}$分数更高。假设${F_1}$分数是结合查准率和查全率的合理方式，你可以快速选出分类器A，淘汰分类器B。

有一个定义明确的开发集用来测量查准率和查全率，再加上这样一个单一数值评估指标，有时我叫单实数评估指标，能让你快速判断分类器A或者分类器B更好。所以有这样一个开发集，加上单实数评估指标，你的迭代速度肯定会很快，

它可以加速改进您的机器学习算法的迭代过程。

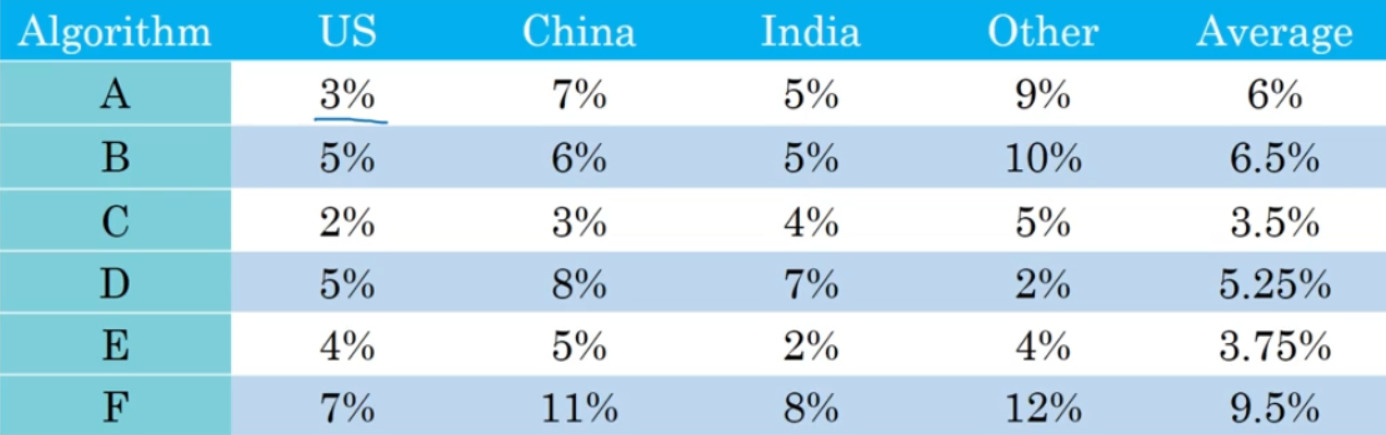
假设你在开发一个猫应用来服务四个地理大区的爱猫人士，美国、中国、印度还有世界其他地区。我们假设你的两个分类器在来自四个地理大区的数据中得到了不同的错误率，比如算法在美国用户上传的图片中达到了 3%错误率，等等。

你的分类器在不同市场和地理大区中的表现应该是有用的，但是通过跟踪四个数字，很难扫一眼这些数值就快速判断算法或算法哪个更好。如果你测试很多不同的分类器，那么看着那么多数字，然后快速选一个最优是很难的。所以在这个例子中，我建议，除了跟踪分类器在四个不同的地理大区的表现，也要算算平均值。假设平均表现是一个合理的单实数评估指标，通过计算平均值，你就可以快速判断。

看起来算法C的平均错误率最低，然后你可以继续用那个算法。你必须选择一个算法，然后不断迭代。