3-9 训练一个 Softmax 分类器

训练一个 Softmax 分类器（ Training a Softmax classifier）

Softmax 这个名称的来源是与所谓hardmax 对比， hardmax会把向量z变成这个向量：

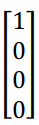
hardmax 函数会观察z的元素，然后在z中最大元素的位置放上 1，其它位置放上 0，所以这是一个 hard max，也就是最大的元素的输出为 1，其它的输出都为 0。与之相反， Softmax 所做的从z到这些概率的映射更为温和。

Softmax 回归或 Softmax 激活函数将logistic 激活函数推广到类，而不仅仅是两类，结果就是如果C=2，那么C=2的 Softmax实际上变回了 logistic 回归。

在 Softmax 分类中，我们一般用到的损失函数是：

$J({w^{[1]}},{b^{[1]}},......) = \frac{1}{m}\sum\limits_{i = 1}^m {L({{\hat y}^{(i)}},{y^{(i)}})}$

损失函数所做的就是它找到你的训练集中的真实类别，然后试图使该类别相应的概率尽可能地高，如果你熟悉统计学中最大似然估计，这其实就是最大似然估计的一种形式。你要做的就是用梯度下降法，使这里的损失最小化。

假设C=4，那么y是一个 4×1 向量 ，如果你实现向量化，矩阵大写 Y就是 $[{y^{(1)}}{y^{(2)}}{y^{(3)}}...{y^{(m)}}]$，那么矩阵Y就是：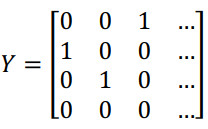

即Y矩阵就是一个4 × m矩阵。类似的：$\hat Y = [{{\hat y}^{(1)}}{{\hat y}^{(2)}}{{\hat y}^{(3)}}...{{\hat y}^{(m)}}]$，${\hat Y}$也是一个 4×m 向量。
最后我们来看一下，在有 Softmax 输出层时如何实现梯度下降法，这个输出层会计算 ${z^{[l]}}$，它是 C×1 维向量。然后你用 Softmax 激活函数来得到${a^{[l]}}$ ，或者说y,然后又能由此计算出损失。
初始化反向传播所需要的关键步骤或者说关键方程是这个表达式 $d{z^{[l]}} = \hat y - y$,其导数为$d{z^{[l]}} = \frac{{\partial J}}{{\partial {z^{[l]}}}}$。