3-5 将 Batch Norm 拟合进神经网络

将 Batch Norm 拟合进神经网络（ Fitting Batch Norm into a neural network）

假设现有如下的神经网络：

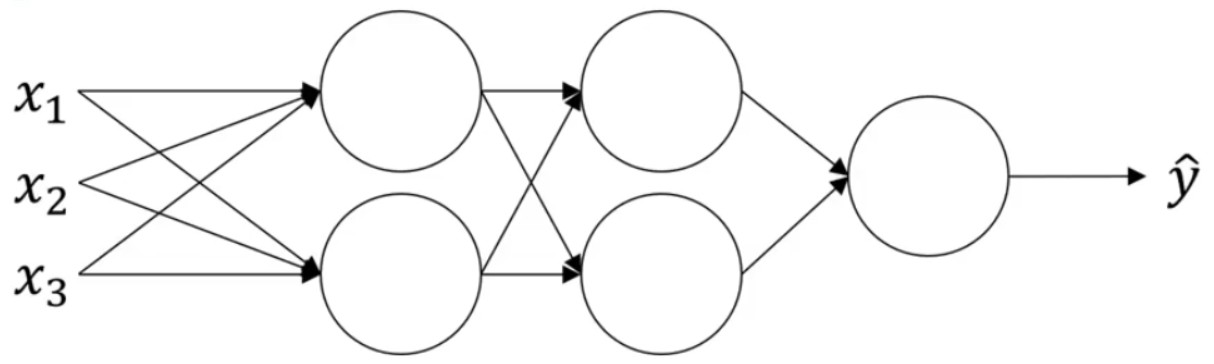
可以认为每个单元负责计算两件事情：第一，先计算z，然后应用到激活函数中再计算a，所以，可以认为，每个圆圈代表着两步计算。

如果没有应用Batch归一化，你会把输入X拟合到第一隐藏层，然后计算${z^{[1]}}$，这是由${w^{[1]}}$和${b^{[1]}}$两个参数控制的。接着，通常而言，会将${z^{[1]}}$拟合到激活函数${a^{[1]}}$。

但Batch归一化的做法是将${z^{[1]}}$值进行Batch归一化，简称BN，此过程由参数${\beta ^{[1]}}$和${\gamma ^{[1]}}$控制的。这一操作将会给你一个新的规范化的${z^{[1]}}$值，称为{{\tilde z}^{[1]}} 然后将其输入激活函数中得到${a^{[1]}}$，即：${a^{[1]}} = {g^{[1]}}({{\tilde z}^{[1]}})$ 。现在，你已在第一层进行了计算，此时 Batch 归一化发生在的计算和之间，接下来，你需要应用${a^{[1]}}$ 值来计算${z^{[2]}}$，此过程是由${w^{[2]}}$和${b^{[2]}}$两个参数控制的。与在第一层所做的类似，你会将${z^{[2]}}$ 进行 Batch 归一化，现在我们简称BN，这是由下一层的 Batch 归一化参数${\beta ^{[2]}}$和${\gamma ^{[2]}}$所管制的，现在你得到${{\tilde z}^{[2]}}$ ，再通过激活函数计算出${a^{[2]}}$等等。

所以，所以需要强调的是 Batch 归一化是发生在计算z和a之间的。除了参数${w^{[l]}}$，${b^{[l]}}$又加入了新的参数${\beta ^{[l]}}$和${\gamma ^{[l]}}$。

所以现在，这是你算法的新参数，接下来你可以使用想用的任何一种优化算法，比如使用梯度下降法来执行它。

举个例子，对于给定层，你会计算$d{\beta ^{[l]}}$ 接着更新参数$\beta$：

${\beta ^{[l]}} = {\beta ^{[l]}} - \alpha d{\beta ^{[l]}}$ 。

当然，你也可以使用 Adam 或 RMSprop 或 Momentum，以更新参数$\beta$和$\ gamma $，并不是只应用梯度下降法。

在 TensorFlow框架中，实现Batch 归一化，你可以用这个函数：tf.nn.batch_normalization

实践中， Batch 归一化通常和训练集的 mini-batch 一起使用。你应用 Batch 归一化的方式就是，你用第一个 mini-batch (${X^{\{ 1\} }}$)，应用参数${w^{[l]}}$和${b^{[l]}}$计算${z^{[1]}}$。

接着Batch 归一化会减去均值，除以标准差，由${\beta ^{[l]}}$和${\gamma ^{[l]}}$ 重新缩放，这样就得到了${{\tilde z}^{[1]}}$，再应用激活函数得到${a^{[1]}}$，然后利用参数${w^{[2]}}$，${b^{[2]}}$计算${z^{[2]}}$，依次类推。这里所有的步骤都是为了在mini-batch (${X^{\{ 1\} }}$)运行一步梯度下降。

按照上述的方法应用到 mini-batch (${X^{\{ 2\} }}$)，mini-batch (${X^{\{ 3\} }}$)。。。

在此需要注意的一个细节是：

每层的计算参数都是：

${w^{[l]}}$，${b^{[l]}}$，${\beta ^{[l]}}$，${\gamma ^{[l]}}$。

${z^{[l]}} = {w^{[l]}}{a^{[1 - 1]}} + {b^{[l]}}$

Batch 归一化做的是：先将${z^{[l]}}$归一化，结果为均值 0 和标准方差，再由$\beta$和$\gamma$重缩放，但这意味着，无论${b^{[l]}}$的值为多少，都会被减去，因为在 Batch 归一化的过程中，你要计算${z^{[l]}}$ 的均值，再减去平均值，在此例中的 mini-batch 中增加任何常数，数值都不会改变，因为加上的任何常数都将会被均值减去所抵消。

所以，如果你在使用 Batch 归一化，其实你可以消除这个参数${b^{[l]}}$，或者你也可以，暂时把它设置为 0，那么，参数变成${z^{[l]}} = {w^{[l]}}{a^{[1 - 1]}}$

，然后你计算归一化的${z^{[l]}}$：

${{\tilde z}^{[l]}} = {\gamma ^{[l]}}{z^{[l]}} + {\beta ^{[l]}}$

所以，${b^{[l]}}$ 这个参数没有意义，你必须去掉它，由${\beta ^{[l]}}$ 代替，这是个控制参数，会影响转移或偏置条件。

总结一下关于如何用 Batch 归一化来应用梯度下降法：

假设你在使用 mini-batch梯度下降法，你运行t = 1到 batch 数量的 for 循环，你会在 mini-batch${X^{\{ t\} }}$上应用正向 prop，每个隐藏层都应用正向 prop，用 Batch 归一化代替${z^{[l]}}$为${{\tilde z}^{[l]}}$。接下来，它确保在这个 mini-batch 中，z值有归一化的均值和方差，归一化均值和方差后是${{\tilde z}^{[l]}}$ ，然后，你用反向 prop 计算：$d{w^{[l]}}$，$d{b^{[l]}}$，$d{\beta ^{[l]}}$ ，$d{\gamma ^{[l]}}$ 尽管严格来说，因为你要去掉b，这部分其实已经去掉了。最后，你更新这些参数：

${w^{[l]}} = {w^{[l]}} - \alpha d{w^{[l]}}$

${\beta ^{[l]}} = {\beta ^{[l]}} - \alpha d{\beta ^{[l]}}$

${\gamma ^{[l]}} = {\gamma ^{[l]}} - \alpha d{\gamma ^{[l]}}$