3-2 为超参数选择合适的范围

为超参数选择合适的范围（ Using an appropriate scale to pick hyperparameters）

随机取值可以提升你的搜索效率。但随机取值并不是在有效范围内的随机均匀取值，而是选择合适的标尺，用于探究这些超参数，这很重要。

假设你要选取隐藏单元的数量${n^{[l]}}$ ，假设，你选取的取值范围是从 50 到 100 中某点，这种情况下，看到这条从 50-100 的数轴，你可以随机在其取点，这是一个搜索特定超参数的很直观的方式。或者，如果你要选取神经网络的层数，我们称之为字母L你也许会选择层数为 2 到 4 中的某个值，接着顺着 2， 3， 4 随机均匀取样才比较合理，你还可以应用网格搜索，你会觉得 2， 3， 4，这三个数值是合理的，这是在几个在你考虑范围内随机均匀取值的例子，这些取值还蛮合理的，但对某些超参数而言不适用。

看看这个例子，假设你在搜索超参数$\alpha$学习速率），假设你怀疑其值最小是 0.0001 或最大是 1。如果你画一条从 0.0001 到 1 的数轴，沿其随机均匀取值，那 90%的数值将会落在0.1 到 1 之间，结果就是，在 0.1 到 1 之间，应用了 90%的资源，而在 0.0001 到 0.1 之间，只有 10%的搜索资源，这看上去不太对：

反而，用对数标尺搜索超参数的方式会更合理，因此这里不使用线性轴，分别依次取0.0001， 0.001， 0.01， 0.1， 1，在对数轴上均匀随机取点，这样，在 0.0001 到 0.001 之间，就会有更多的搜索资源可用，还有在 0.001 到 0.01 之间等等。

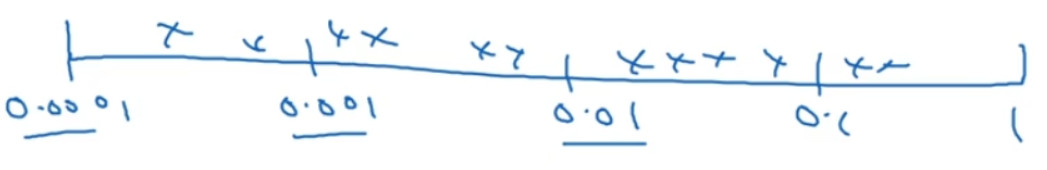
在python中r=-4*np.random.rand()，这行可以得出$r \in [4,0]$,那么$\alpha$，所以最左边的数字是${10^0}$,然后$\alpha$随机取值，$\alpha {\rm{ = }}{10^{\rm{r}}}$。

更常见的情况是，如果你在${10^a}$和${10^b}$之间取值，在此例中，${10^a}$（ 0.0001），你可以通过0.0001算出${10^a}$的值，即-4，在右边的值是${10^b}$,你可以算出b的值1，即 0。你要做的就是在[a,b] 区间随机均匀地给r取值，这个例子中$r \in [ - 4,0]$ ，然后你可以设置$\alpha$的值，基于随机取样的超参数$\alpha {\rm{ = }}{10^{\rm{r}}}$。

所以总结一下，在对数坐标下取值，取最小值的对数就得到a的值，取最大值的对数就得到b值，所以现在你在对数轴上的${10^a}$到${10^b}$区间取值，在a，b间随意均匀的选取r值，将超参数设置为${10^{\rm{r}}}$，这就是在对数轴上取值的过程。

另一个棘手的例子是给$\beta$取值，用于计算指数的加权平均值。 假设你认为$\beta$是 0.9到 0.999 之间的某个值，也许这就是你想搜索的范围。记住这一点，当计算指数的加权平均值时，取 0.9 就像在 10 个值中计算平均值，有点类似于计算 10 天的温度平均值，而取 0.999就是在 1000 个值中取平均。

如果你想在 0.9 到 0.999 区间搜索，那就不能用线性轴取值。要随机均匀在此区间取值，所以考虑这个问题最好的方法就是，我们要探究的是$1 - \beta $，此值在 0.1 到 0.001 区间内，所以我们会给$1 - \beta $取值，大概是从 0.1 到 0.001，应用之前幻灯片中介绍的方法，这是${10^{ - 1}}$，${10^{ - 3}}$。值得注意的是，在之前的幻灯片里，我们把最小值写在左边，最大值写在右边，但在这里，我们颠倒了大小。

$\beta$接近 1 时，所得结果的灵敏度会变化，即使$\beta$有微小的变化。所以$\beta$在 0.9 到 0.9005 之间取值，无关紧要，你的结果几乎不会变化。但$\beta$值如果在 0.999 到 0.9995 之间，这会对你的算法产生巨大影响。

根据公式$\frac{1}{{1 - \beta }}$，当$\beta$为0.999时，基于 1000 个值。而当当$\beta$为0.9995时，基于 2000 个值。

所以整个取值过程中，你需要更加密集地取值，在$\beta$接近 1 的区间内，或者说，当$1 - \beta $接近于 0时，这样，你就可以更加有效的分布取样点，更有效率的探究可能的结果。