3-1 调试处理

调试处理（ Tuning process）

按照参数的重要性依次排列：

• 学习速率$\alpha$
• Momentum（动量梯度下降法）的参数$\beta$

如果使用Adam 优化算法的参数${\beta _1}$，${\beta _2}$，$\varepsilon $，但是通常使用默认值：0.9,0.999，${10^{{\rm{ - }}8}}$

• mini-batch 的大小
• 不同层中隐藏单元的数量
• 层数
• 学习率衰减率

在早一代的机器学习算法中，如果你有两个超参数，这里我会称之为超参 1，超参 2，常见的做法是在网格中取样点，像这样，然后系统的研究这些数值。这里我放置的是 5×5 的网格，实践证明，网格可以是 5×5，也可多可少，但对于这个例子，你可以尝试这所有的 25 个点，然后选择哪个参数效果最好。当参数的数量相对较少时，这个方法很实用：

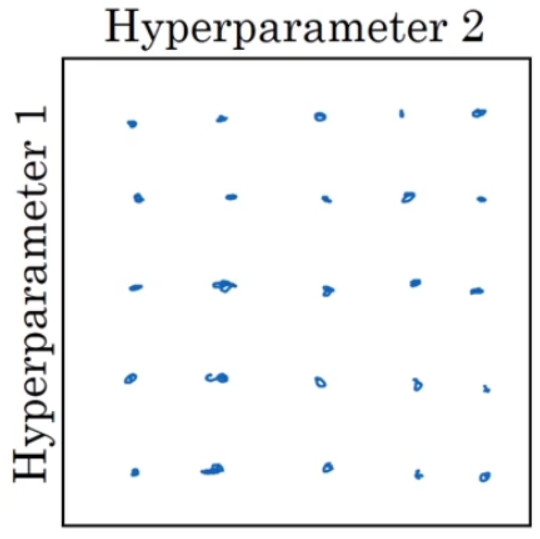
在深度学习领域，采用下面的做法，随机选择点，所以你可以选择同等数量的点， 25 个点， 接着，用这些随机取的点试验超参数的效果。之所以这么做是因为，对于你要解决的问题而言，你很难提前知道哪个超参数最重要，正如你之前看到的，一些超参数的确要比其它的更重要。

举个例子，假设超参数1是$\alpha $（学习速率），取一个极端的例子，假设超参数 2 是 Adam算法中，分母中的$\varepsilon $在这种情况下，$\alpha $取值很重要，而$\varepsilon $值则无关紧要。如果你在网格中取点，接着，你试验了$\alpha $的5 个取值，那你会发现，无论$\varepsilon $何值，结果基本上都是一样的。所以，你知道共有 25 种模型，但进行试验的$\alpha $只有 5 个。

对比而言，如果你随机取值，你会试验 25 个独立的$\alpha $，似乎你更有可能发现效果做好的那个。

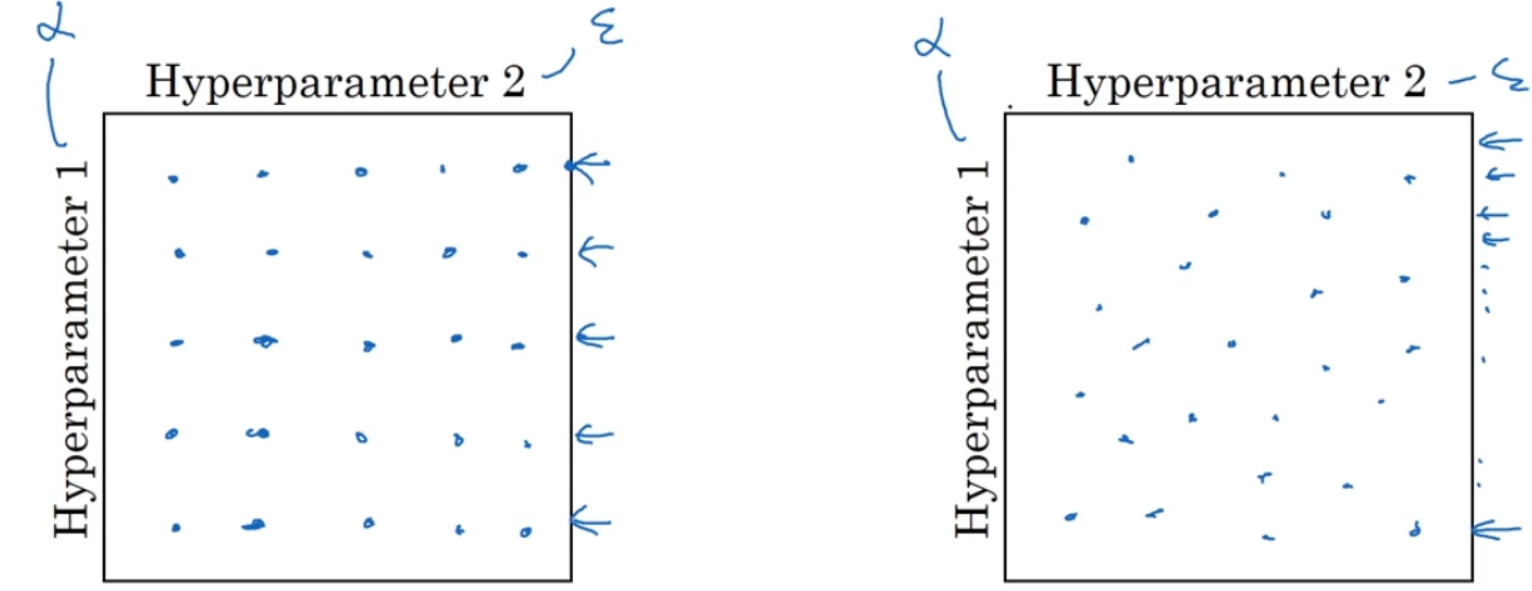
假如，你有三个超参数，这时你搜索的不是一个方格，而是一个立方体，超参数 3 代表第三维，接着，在三维立方体中取值，你会试验大量的更多的值，三个超参数中每个都是。

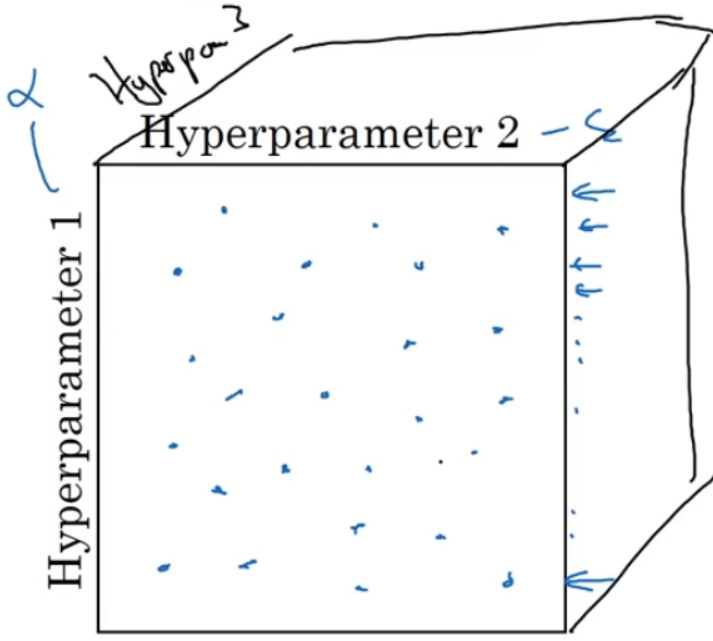
实践中，你搜索的可能不止三个超参数有时很难预知，哪个是最重要的超参数，对于你的具体应用而言，随机取值而不是网格取值表明，你探究了更多重要超参数的潜在值，无论结果是什么。当你给超参数取值时，另一个惯例是采用由粗糙到精细的策略：

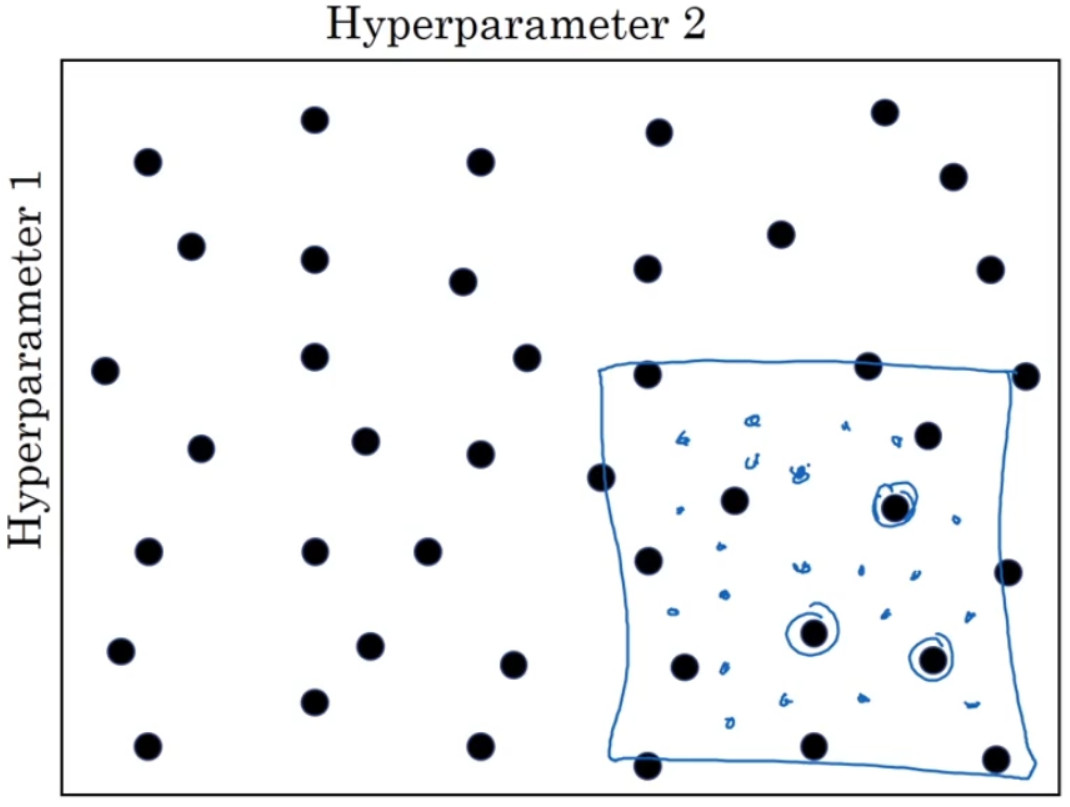
比如在二维的那个例子中，你进行了取值，也许你会发现效果最好的某个点，也许这个点周围的其他一些点效果也很好，那在接下来要做的是放大这块小区域（小蓝色方框内），然后在其中更密集得取值或随机取值，聚集更多的资源，在这个蓝色的方格中搜索，如果你怀疑这些超参数在这个区域的最优结果，那在整个的方格中进行粗略搜索后，你会知道接下来应该聚焦到更小的方格中。在更小的方格中，你可以更密集得取点。所以这种从粗到细的搜索也经常使用。