2-9 局部最优的问题

局部最优的问题(The problem of local optima)

人们总是担心优化算法会困在极差的局部最优， 不过随着深度学习理论不断发展，我们对局部最优的理解也发生了改变。

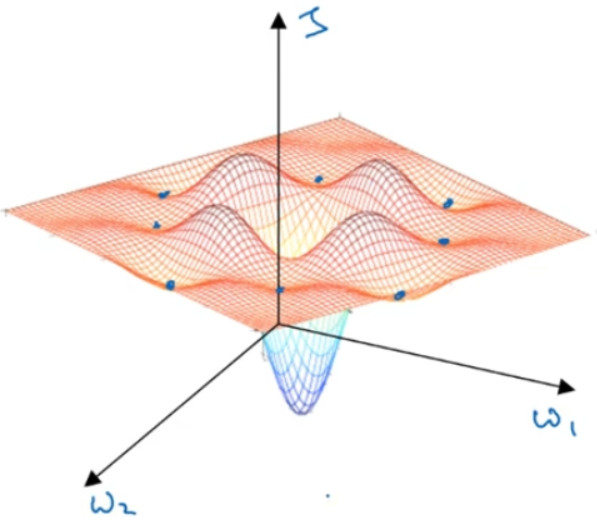
这是曾经人们在想到局部最优时脑海里会出现的图，也许你想优化一些参数，我们把它们称之为${W_1}$和${W_2}$，平面的高度就是损失函数。在图中似乎各处都分布着局部最优。梯度下降法或者某个算法可能困在一个局部最优中，而不会抵达全局最优。如果你要作图计算一个数字，比如说这两个维度，就容易出现有多个不同局部最优的图，而这些低维的图曾经影响了我们的理解，但是这些理解并不正确。事实上，如果你要创建一个神经网络，通常梯度为零的点并不是这个图中的局部最优点，实际上成本函数的零梯度点，通常是鞍点。

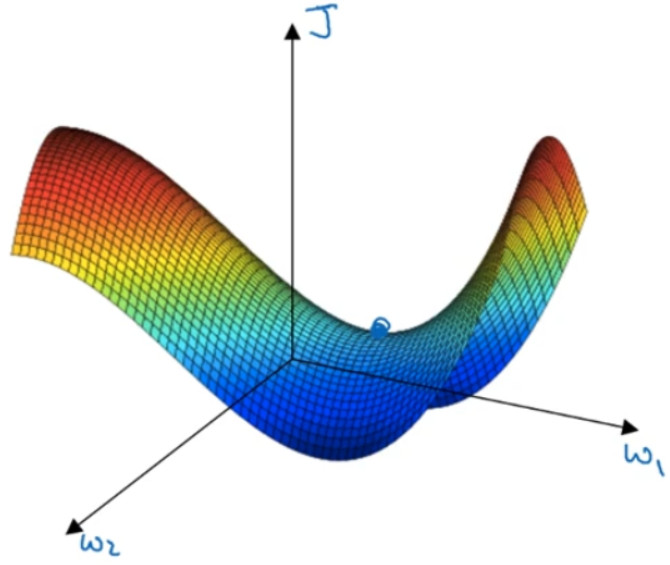
但是一个具有高维度空间的函数，如果梯度为 0，那么在每个方向，它可能是凸函数，也可能是凹函数。如果你在 2 万维空间中，那么想要得到局部最优，所有的 2 万个方向都需要是这样，但发生的机率也许很小，也许是${2^{ - 20000}}$，你更有可能遇到有些方向的曲线会这样向上弯曲，另一些方向曲线向下弯，而不是所有的都向上弯曲，因此在高维度空间，你更可能碰到鞍点，而不会碰到局部最优。

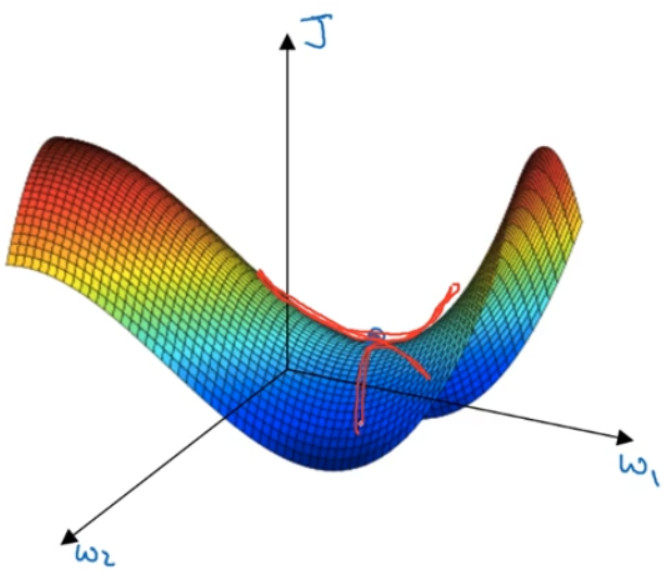
由上图我们可以分析是平稳段会减缓学习，平稳段是一块区域，其中导数长时间接近于 0，如果你在此处，梯度会从曲面从从上向下下降，因为梯度等于或接近 0，曲面很平坦，你得花上很长时间慢慢抵达平稳段的这个点。

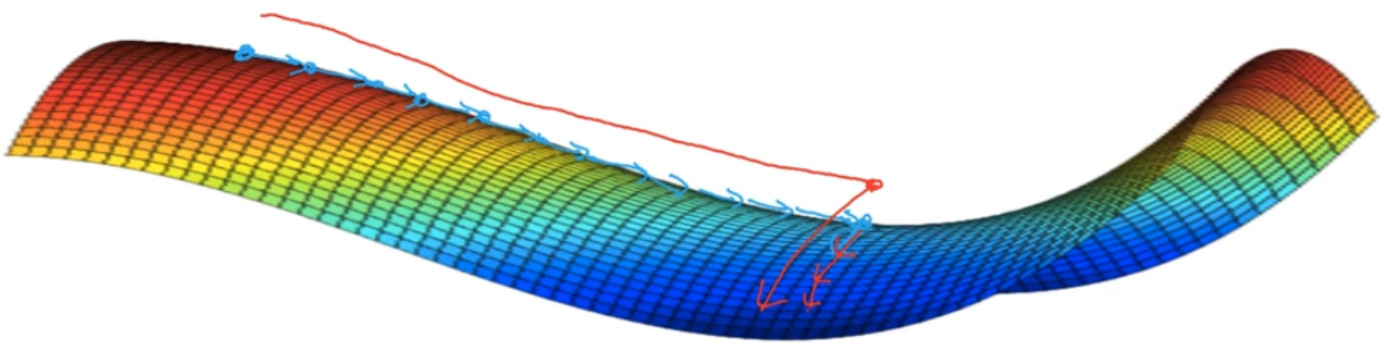
总结：

你不太可能困在极差的局部最优中，条件是你在训练较大的神经网络，存在大量参数， 并且成本函数J被定义在较高的维度空间。

平稳段是一个问题，这样使得学习十分缓慢，这也是像 Momentum 或是RMSprop， Adam 这样的算法，能够加速学习算法的地方。在这些情况下，更成熟的优化算法，如 Adam 算法，能够加快速度，让你尽早往下走出平稳段。