2-8 学习率衰减

学习率衰减(Learning rate decay)

加快学习算法的一个办法就是随时间慢慢减少学习率，我们将之称为学习率衰减。

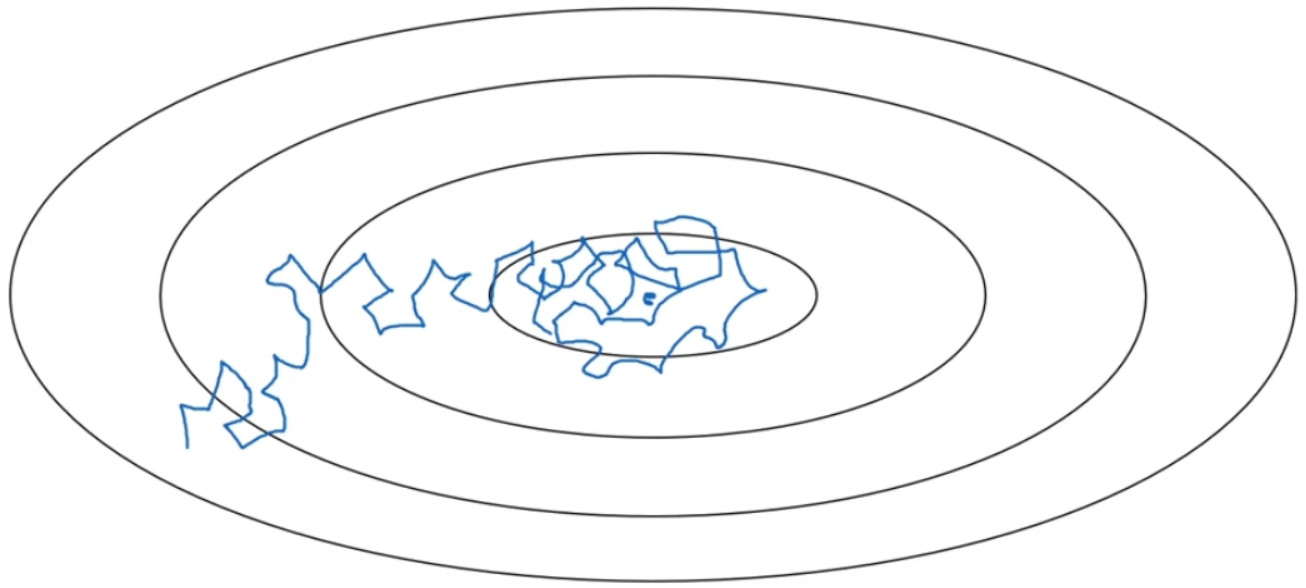
假设你要使用 mini-batch 梯度下降法， mini-batch 数量不大，大概 64 或者 128 个样本，在迭代过程中会有噪音（ 蓝色线），下降朝向这里的最小值，但是不会精确地收敛，所以你的算法最后在附近摆动，并不会真正收敛，因为你用的a是固定值，不同的 mini-batch 中有噪音。

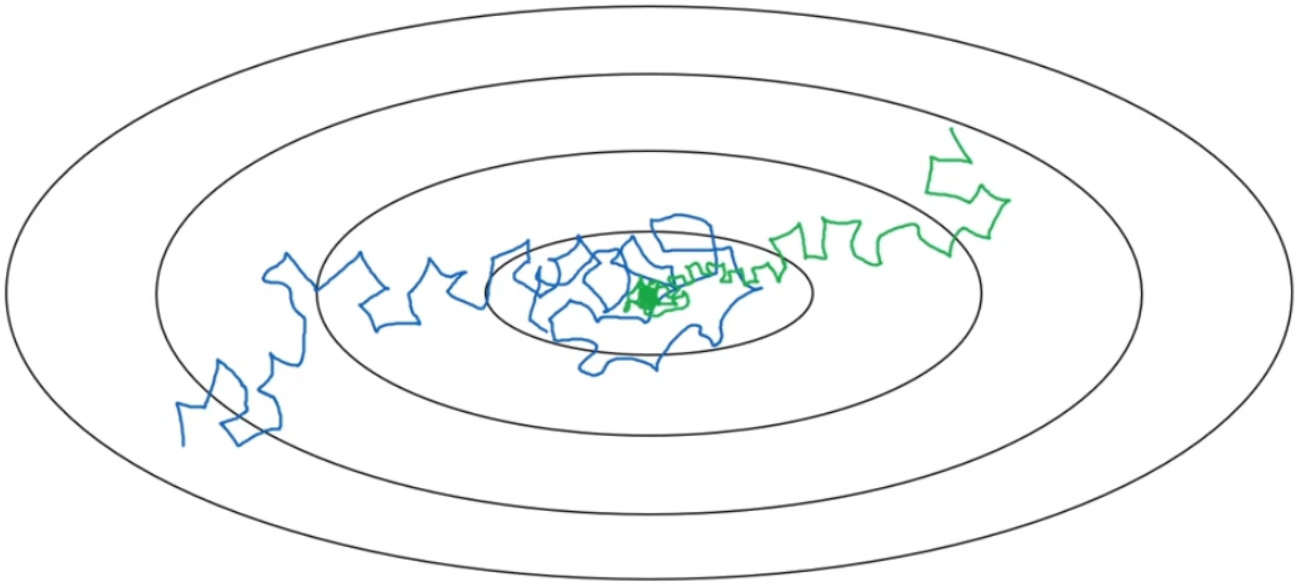
但要慢慢减少学习率a的话，在初期的时候，a学习率还较大，学习还是相对较快，但随着a变小，你的步伐也会变慢变小，所以最后你的曲线（绿色线）会在最小值附近的一小块区域里摆动，而不是在训练过程中，大幅度在最小值附近摆动。

所以慢慢减少的本质在于，在学习初期，你能承受较大的步伐，但当开始收敛的时候，小一些的学习率能让你步伐小一些。

如果你有以下这样的训练集，拆分成不同的 mini-batch，第一次遍历训练集叫做第一代。第二次就是第二代，依此类推。

、、

你可以将a设置为：

$a = \frac{1}{{1 + decayrate*epoch - num}}{a_0}$

decay-rate 称为衰减率， epoch-num 为代数，${a_0}$为初始学习率，注意这个衰减率是另一个你需要调整的超参数。

这里有一个具体例子，如果你计算了几代，也就是遍历了几次，如果${a_0}$为 0.2，衰减率decay-rate 为 1， 那么在第一代中，$a = \frac{1}{{1 + 1}}{a_0} = 0.1$，在第二代学习率为0.067，第三代变成0.05，第四代为0.04。

学习率呈递减趋势。如果你想用学习率衰减，要做的是要去尝试不同的值，包括超参数${a_0}$以及超参数衰退率，找到合适的值，除了这个学习率衰减的公式，人们还会用其它的公式：

$a = {0.95^{epoch - num}}{a_0}$

$a = \frac{k}{{\sqrt {^{epoch - num}} }}{a_0}$

$a = \frac{k}{{\sqrt t }}{a_0}$  （t为mini-batch 的数字）

离散下降（ discrete stair cease）: 也就是某个步骤有某个学习率，一会之后，学习率减少了一半，一会儿减少一半，一会儿又一半。

手动衰减：如果你一次只训练一个模型， 如果你要花上数小时或数天来训练，有些人的确会这么做，看看自己的模型训练，耗上数日，然后他们觉得，学习速率变慢了，我把调小一点。手动控制当然有用，时复一时，日复一日地手动调整，只有模型数量小的时候有用，但有时候人们也会这么做。