2-5 动量梯度下降法

动量梯度下降法（Gradient descent with Momentum）

还有一种算法叫做 Momentum，或者叫做动量梯度下降法，运行速度几乎总是快于标准的梯度下降算法，简而言之，基本的想法就是计算梯度的指数加权平均数，并利用该梯度更新你的权重。

如果你要优化成本函数，函数形状如图，红点代表最小值的位置，利用梯度下降：

如果进行梯度下降法的一次迭代，无论是 batch 或 mini-batch下降法，可以看到是慢慢摆动到最小值，这种上下波动减慢了梯度下降法的速度，你就无法使用更大的学习率，如果你要用较大的学习率（紫色箭头），结果可能会偏离函数的范围，为了避免摆动过大，你要用一个较小的学习率。

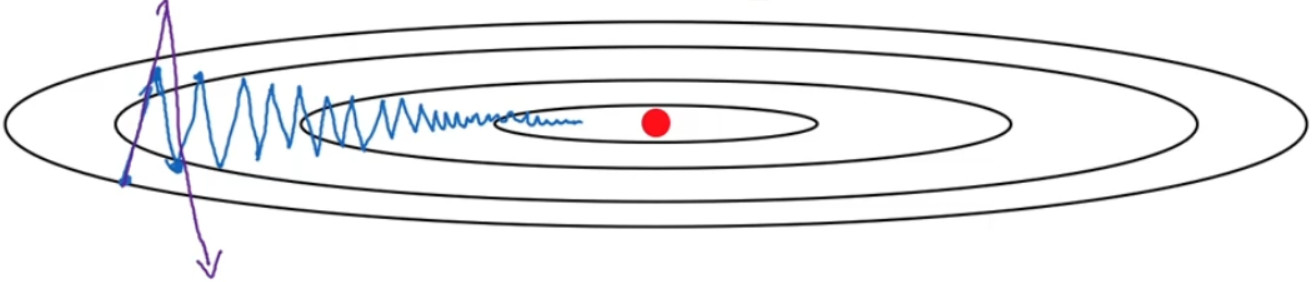
理想的情况是，在纵轴上，你希望学习慢一点，因为你不想要这些摆动，但是在横轴上，你希望加快学习，你希望快速从左向右移，移向最小值，移向红点。所以使用动量梯度下降法，你需要做的是，在每次迭代中，确切来说在第t次迭代的过程中，你会计算微分$dW$，$db$，你要做的是计算：

$vdw = \beta vdw + (1 - \beta )dW$

$vdb = \beta vdb + (1 - \beta )db$

然后重新赋值权重:

$W: = W - \alpha vdw$

$b: = b - \alpha vdb$

这样就可以减缓梯度下降的幅度。

你会发现这些纵轴上的摆动平均值接近于零，所以在纵轴方向，你希望放慢一点，平均过程中，正负数相互抵消，所以平均值接近于零。但在横轴方向，所有的微分都指向横轴方向，因此横轴方向的平均值仍然较大，因此用算法几次迭代后，你发现动量梯度下降法，最终纵轴方向的摆动变小了，横轴方向运动更快，因此你的算法走了一条更加直接的路径，在抵达最小值的路上减少了摆动。

具体的计算步骤：

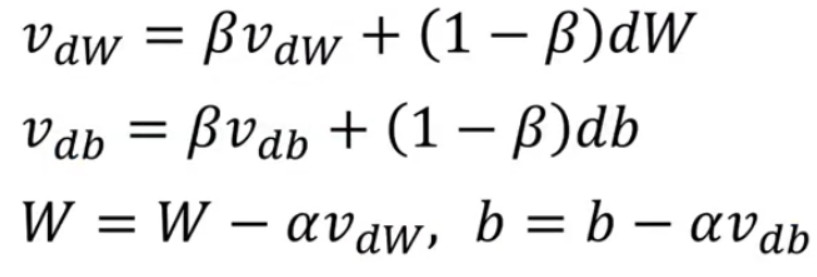
这里有两个超参数$\alpha$和$\beta $，$\beta $控制着指数加权平均数。最常用的值是0.9，即现在平均了前十次迭代的梯度。实际上$\beta $为 0.9时，效果不错，你可以尝试不同的值，可以做一些超参数的研究，不过 0.9 是很棒的鲁棒数。

关于偏差修正，要拿$vdw$，$vdb$除以$1 - {\beta ^t}$，实际上人们不这么做，因为 10 次迭代之后，因为你的移动平均已经过了初始阶段。实际中，在使用梯度下降法或动量梯度下降法时，人们不会受到偏差修正的困扰。

$vdw$的初始值是0，它的维度与dW和W相同；

$vdb$的初始值是0，它的维度与db和b相同。

在一些资料中，也有删除$(1 - \beta )$，所以$vdw$缩小了$(1 - \beta )$倍，相当于乘以$\frac{1}{{1 - \beta }}$，所以你要用梯度下降最新值的话，$\alpha$要根据$\frac{1}{{1 - \beta }}$相应变化。实际上，二者效果都不错， 只会影响到学习率

$\alpha $的最佳值。我觉得这个公式用起来没有那么自然，因为有一个影响，如果你最后要调整超参数，$\beta $，就会影响到$vdw$和$vdb$你也许还要修改学习率$\alpha$，所以最好使用没有删除$(1 - \beta )$情况下的公式。

所以这就是动量梯度下降法，这个算法肯定要好于没有 Momentum 的梯度下降算法。