2-4 指数加权平均的偏差修正

指数加权平均的偏差修正（ Bias correction in exponentially weighted averages）

实际上$\beta {\rm{ = }}0.98$时，图中所示的划线并不是绿色的线，而是下图紫色的线条：

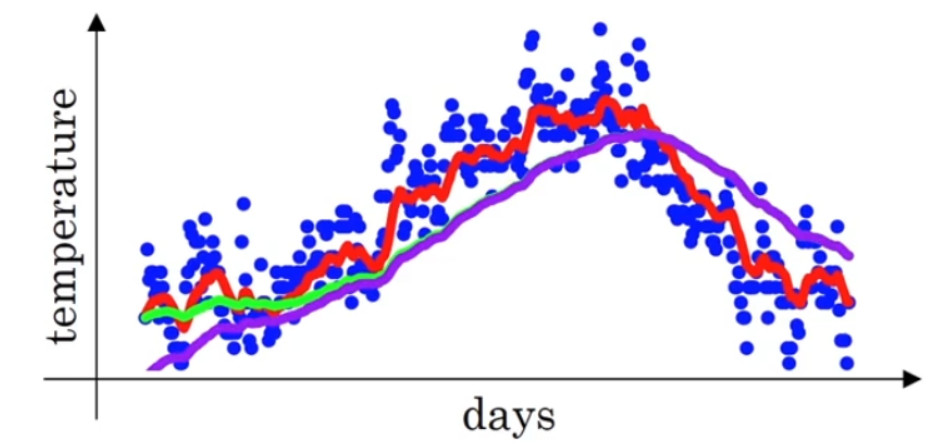
可以注意到紫色曲线的起点较低。

计算移动平均数的时候，初始化${v_0} = 0$，${v_1} = 0.98{v_0} + 0.02{\theta _1}$，但是${v_0} = 0$，所以这部分没有了$0.98{v_0}$，所以${v_1} = 0.02{\theta _1}$所以如果一天温度是 40 华氏度，那么${v_1} = 0.02{\theta _1} = 0.02*40 = 8$，因此得到的值会小很多，所以第一天温度的估测不准。

${v_2} = 0.98{v_1} + 0.02{\theta _2}$，如果代入${v_1}$，然后相乘，所以${v_2} = 0.98*0.02{\theta _1} + 0.02{\theta _2} = 0.0196{\theta _1} + 0.02{\theta _2}$，假设${\theta _1}$和${\theta _2}$都是正数，计算后${v_2}$要远小于${\theta _1}$和${\theta _2}$，所以${v_2}$不能很好估测出这一年前两天的温度。

有个办法可以修改这一估测，让估测变得更好，更准确，特别是在估测初期，也就是不用${v_t}$，而是用$\frac{{{v_t}}}{{1 - {\beta ^t}}}$，t就是现在的天数。举个具体例子：

当$t = 2$，$\frac{{{v_2}}}{{1 - {\beta ^2}}} = \frac{{0.0196{\theta _1} + 0.02{\theta _2}}}{{1 - {{0.98}^2}}} = \frac{{0.0196{\theta _1} + 0.02{\theta _2}}}{{0.0396}}$也就是${\theta _1}$，${\theta _2}$的加权平均数，并去除偏差。

你会发现随着t增加，${{\beta ^t}}$接近于 0，所以当t很大的时候，偏差修正几乎没有作用，因此当t较大的时候，紫线基本和绿线重合了。不过在开始学习阶段，你才开始预测热身练习，偏差修正可以帮助你更好预测温度，偏差修正可以帮助你使结果从紫线变成绿线。

在机器学习中，在计算指数加权平均数的大部分时候，大家不在乎执行偏差修正，因为大部分人宁愿熬过初始时期，拿到具有偏差的估测，然后继续计算下去。如果你关心初始时期的偏差，在刚开始计算指数加权移动平均数的时候，偏差修正能帮助你在早期获取更好的估测。