2-2 理解 mini-batch 梯度下降法

理解 mini-batch 梯度下降法（ Understanding mini-batch gradient descent）

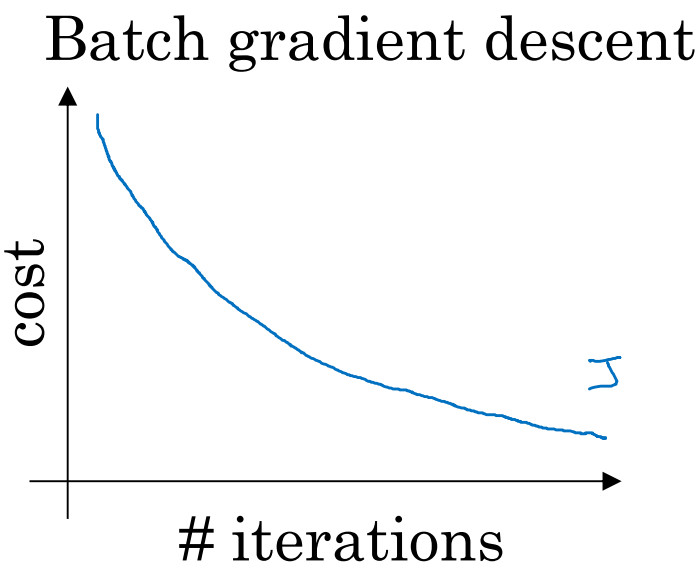
使用 batch 梯度下降法时，每次迭代你都需要历遍整个训练集，可以预期每次迭代成本都会下降，所以如果成本函数J是迭代次数的一个函数，它应该会随着每次迭代而减少，如果在某次迭代中增加了，那肯定出了问题，也许你的学习率太大。

使用 mini-batch 梯度下降法，如果你作出成本函数在整个过程中的图，则并不是每次迭代都是下降的，特别是在每次迭代中，你要处理的是${{\rm{X}}^{\{ t\} }}$和${Y^{\{ t\} }}$如果要作出成本函数${J^{\{ t\} }}$的图，很可能会看到这样的结果，走向朝下，但有更多的噪声。没有每次迭代都下降是不要紧的，但走势应该向下，噪声产生的原因在于也许${{\rm{X}}^{\{ 1\} }}$，${{\rm{Y}}^{\{ 1\} }}$是比较容易计算的 mini-batch，因此成本会低一些。不过也许出于偶然，${{\rm{X}}^{\{ 2\} }}$，${{\rm{Y}}^{\{ 2\} }}$是比较难运算的 mini-batch，或许你需要一些残缺的样本，这样一来，成本会更高一些，所以才会出现这些摆动， 因为你是在运行 mini-batch 梯度下降法作出成本函数图。

你需要决定的变量之一是 mini-batch 的大小，m就是训练集的大小，极端情况下:

如果 mini-batch 的大小等于m，其实就是 batch 梯度下降法，在这种极端情况下，你就有了 mini-batch${{\rm{X}}^{\{ 1\} }}$和${{\rm{Y}}^{\{ 1\} }}$，并且该 mini-batch 等于整个训练集，所以把 mini-batch 大小设为m可以得到 batch 梯度下降法。

另一个极端情况，假设 mini-batch 大小为 1，就有了新的算法，叫做随机梯度下降法，每个样本都是独立的 mini-batch，当你看第一个 mini-batch，也就是mini-batch${{\rm{X}}^{\{ 1\} }}$和${{\rm{Y}}^{\{ 1\} }}$，如果 mini-batch 大小为 1，它就是你的第一个训练样本，这就是你的第一个训练样本。接着再看第二个 mini-batch，也就是第二个训练样本，采取梯度下降步骤，然后是第三个训练样本，以此类推，一次只处理一个。

如果这是你想要最小化的成本函数的轮廓，最小值在那里，在两种极端下成本函数的优化情况：

batch 梯度下降法从某处开始，相对噪声低些，幅度也大一些，你可以继续找最小值。

在随机梯度下降法中，从某一点开始，我们重新选取一个起始点，每次迭代，只对一个样本进行梯度下降，大部分时候你向着全局最小值靠近，有时候你会远离最小值，因为那个样本恰好给你指的方向不对，因此随机梯度下降法是有很多噪声的，平均来看，它最终会靠近最小值，不过有时候也会方向错误，因为随机梯度下降法永远不会收敛，而是会一直在最小值附近波动，但它并不会在达到最小值并停留在此。

实际上你选择的 mini-batch 大小在二者之间，大小在 1 和m之间，而 1 太小了，m太大了，原因在于如果使用 batch 梯度下降法， mini-batch 的大小为m，每个迭代需要处理大量训练样本，该算法的主要弊端在于特别是在训练样本数量巨大的时候，单次迭代耗时太长。如果训练样本不大， batch 梯度下降法运行地很好。

相反，如果使用随机梯度下降法，如果你只要处理一个样本，那这个方法很好，这样做没有问题，通过减小学习率，噪声会被改善或有所减小，但随机梯度下降法的一大缺点是，你会失去所有向量化带给你的加速，因为一次性只处理了一个训练样本，这样效率过于低下，所以实践中最好选择不大不小的 mini-batch 尺寸，实际上学习率达到最快。你会发现两个好处，一方面，你得到了大量向量化，上个视频中我们用过的例子中，如果 mini-batch 大小为1000 个样本，你就可以对 1000 个样本向量化，比你一次性处理多个样本快得多。另一方面，你不需要等待整个训练集被处理完就可以开始进行后续工作，再用一下上个视频的数字，每次训练集允许我们采取 5000 个梯度下降步骤，所以实际上一些位于中间的 mini-batch 大小效果最好。

用 mini-batch 梯度下降法，我们从这里开始，一次迭代这样做，两次，三次，四次，它不会总朝向最小值靠近，但它比随机梯度下降要更持续地靠近最小值的方向，它也不一定在很小的范围内收敛或者波动，如果出现这个问题，可以慢慢减少学习率。

首先，如果训练集较小，直接使用 batch 梯度下降法，样本集较小就没必要使用 mini batch 梯度下降法，你可以快速处理整个训练集，所以使用 batch 梯度下降法也很好，这里的少是说小于 2000 个样本，这样比较适合使用 batch 梯度下降法。不然，样本数目较大的话，一般的 mini-batch 大小为 64 到 512，考虑到电脑内存设置和使用的方式，如果 mini batch 大小是 2 的次方，代码会运行地快一些， 64 就是 2 的 6 次方，以此类推， 128 是 2 的7 次方， 256 是 2 的 8 次方， 512 是 2 的 9 次方。所以我经常把 mini-batch 大小设成 2 的次方。在上一个视频里，我的 mini-batch 大小设为了 1000，建议你可以试一下 1024，也就是2 的 10 次方。也有 mini-batch 的大小为 1024，不过比较少见， 64 到 512 的 mini-batch 比较常见。

最后需要注意的是在你的 mini-batch 中，要确保${{\rm{X}}^{\{ 1\} }}$和${{\rm{Y}}^{\{ 1\} }}$要符合 CPU/GPU 内存，取决于你的应用方向以及训练集的大小。如果你处理的 mini-batch 和 CPU/GPU 内存不相符，不管你用什么方法处理数据，你会注意到算法的表现急转直下变得惨不忍睹，所以我希望你对一般人们使用的 mini-batch 大小有一个直观了解。事实上 mini-batch 大小是另一个重要的变量，你需要做一个快速尝试，才能找到能够最有效地减少成本函数的那个，我一般会尝试几个不同的值，几个不同的 2 次方，然后看能否找到一个让梯度下降优化算法最高效的大小。