1-12 梯度的数值逼近

梯度的数值逼近（ Numerical approximation of gradients）

在实施 backprop 时，有一个测试叫做梯度检验，它的作用是确保 backprop 正确实施。因为有时候，你虽然写下了这些方程式，却不能 100%确定执行 backprop 的所有细节都是正确的。为了逐渐实现梯度检验，先要了解如何计算梯度的数值逼近。

函数f，标记为$f(\theta )$，$f(\theta ) = {\theta ^3}$。

单边公差：

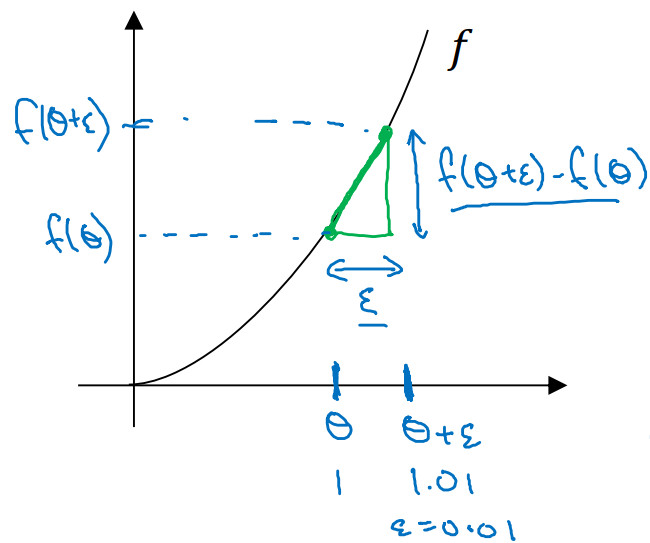
$\frac{{f(\theta  + \varepsilon ) - f(\theta )}}{\varepsilon }$。单边公差的逼近误差：$O(\varepsilon )$

双边公差：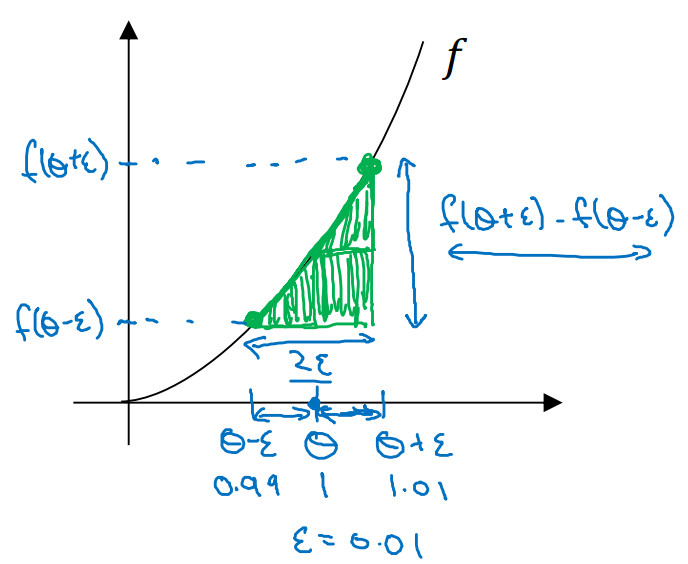

$\frac{{f(\theta  + \varepsilon ) - f(\theta  - \varepsilon )}}{{2\varepsilon }}$，它的期望值接近$g(\theta )$ 。使用双边误差的方法更逼近导数 ，在梯度检验和反向传播中使用该方法时，最终，它与运行两次单边公差的速度一样，实际上，我认为这种方法还是非常值得使用的，因为它的结果更准确。
双边公差的逼近误差：$O({\varepsilon ^2})$