1-10 梯度消失/梯度爆炸

梯度消失/梯度爆炸（ Vanishing / Exploding gradients）

训练神经网络，尤其是深度神经所面临的一个问题就是梯度消失或梯度爆炸，也就是你训练神经网络的时候，导数或坡度有时会变得非常大，或者非常小，甚至于以指数方式变小，这加大了训练的难度。

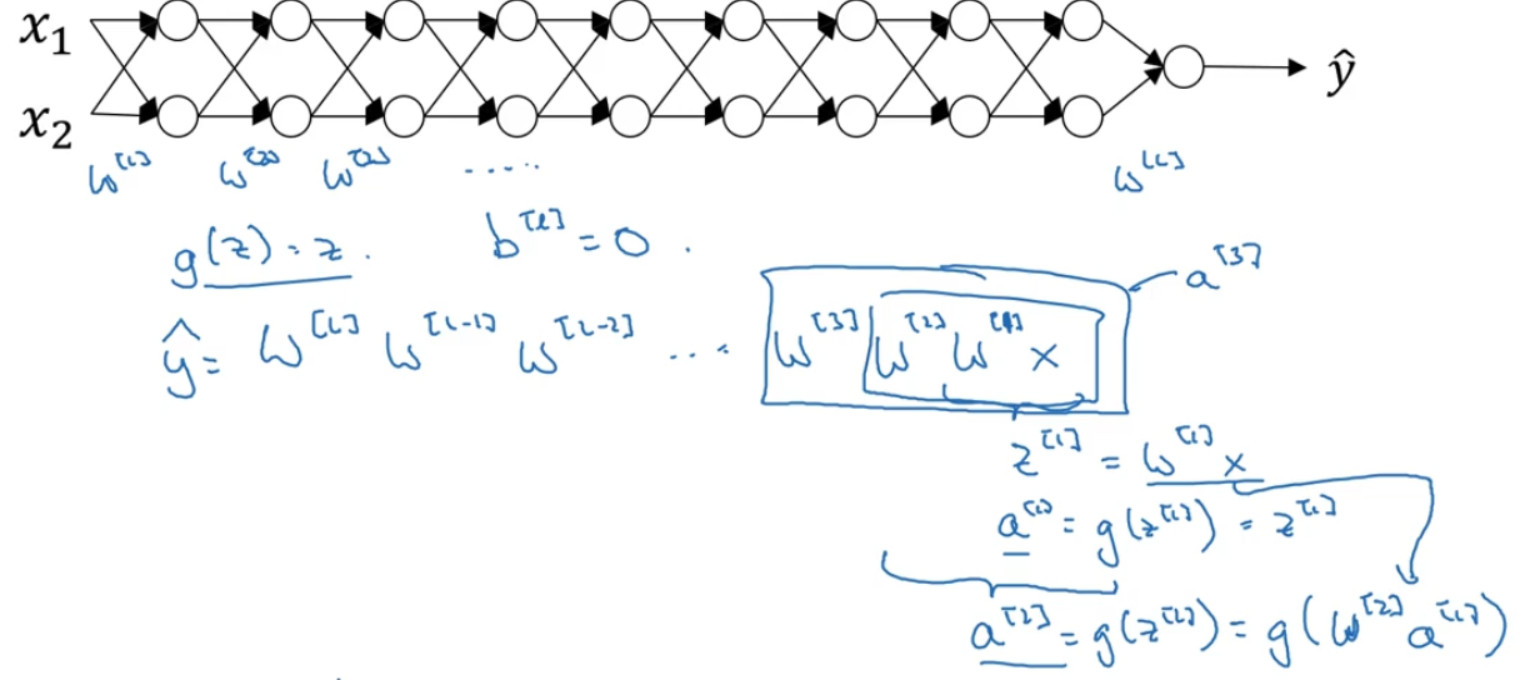
假设你正在训练这样一个极深的神经网络 ，神经网络每层只有两个隐藏单元 g(z)=z,也就是线性激活函数，我们忽略 b,${b^{[l]}} = 0$如果那样的话，输出： 

${\rm{y}} = {W^{[l]}}{W^{[l - 1]}}{W^{[l - 2]}}...{W^{[3]}}{W^{[2]}}{W^{[1]}}x$
因为 b=0，所以：

${W^{[1]}}x = {z^{[1]}}$，${a^{[1]}} = g({z^{[1]}})$，所以：
${W^{[1]}}x = {a^{[1]}}$

同理：

${W^{[2]}}{W^{[1]}}x = {a^{[2]}}$

${W^{[3]}}{W^{[2]}}{W^{[1]}}x = {a^{[3]}}$

所以最终实际上：

${\rm{\hat y}} = {W^{[l]}}{W^{[l - 1]}}{W^{[l - 2]}}...{W^{[3]}}{W^{[2]}}{W^{[1]}}x$

假设每个权重矩阵为：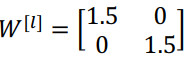

从技术上来讲，最后一项有不同维度，可能它就是余下的权重矩阵，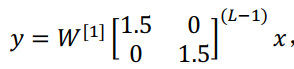

最后的结果：$\hat y$也就是${1.5^{(L - 1)}}x$，如果对于一个深度神经网络来说 L值较大，那么 $\hat y$的值也会非常大，实际上它呈指数级增长的，它增长的比率是${1.5^L}$，因此对于一个深度神经网络，y的值将爆炸式增长。

相反的，如果权重是 0.5：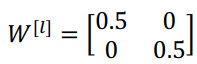

它比 1 小，这项也就变成了 ${0.5^{(L - 1)}}x$，在深度网络中，激活函数以指数级递减。

只虽然这里只是讨论了激活函数与L相关的指数级数增长或下降，它也适用于与层数L相关的导数或梯度函数，也是呈指数级增长或呈指数递减。
在深度神经网络中，如果激活函数或梯度函数以与L相关的指数增长或递减，它们的值将会变得极大或极小，从而导致训练难度上升。