1-9 归一化输入

归一化输入（ Normalizing inputs）

训练神经网络，其中一个加速训练的方法就是归一化输入。
归一化的两个步骤：

• 零均值
• 归一化方差

第一步是零均值化， $u = \frac{1}{m}\sum\nolimits_{i = 1}^m {{x^{(i)}}}$，它是一个向量，x等于每个训练数据x减去u，意思是移动训练集，直到它完成零均值化。
第二部就是归一化方差，${\sigma ^2} = \frac{1}{m}\sum\nolimits_{i = 1}^m {({x^{(i)}}} {)^2}$，${\sigma ^2}$是一个向量，把所有的数据除以${\sigma ^2}$。

假设输入特征有两个，则整个过程的示意如下图所示：

为什么使用归一化

代价函数：

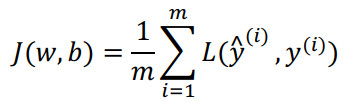
如果你使用非归一化的输入特征，代价函数会像这样：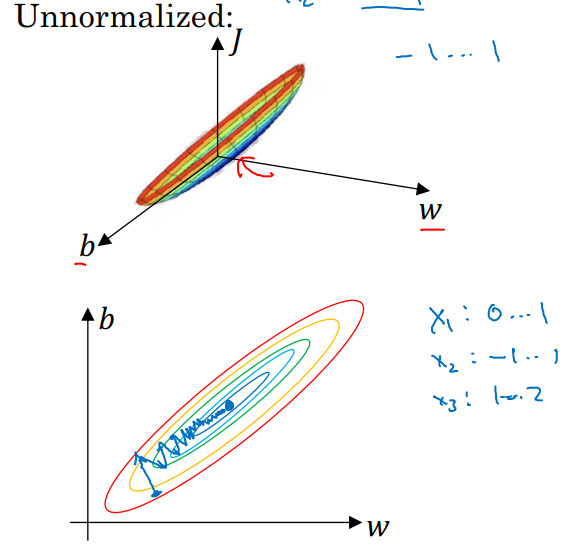

 

代价函数就有点像狭长的碗一样，如果你在上图这样的代价函数上运行梯度下降法，你必须使用一个非常小的学习率。因为如果是在这个位置，梯度下降法可能需要多次迭代过程，直到最后找到最小值。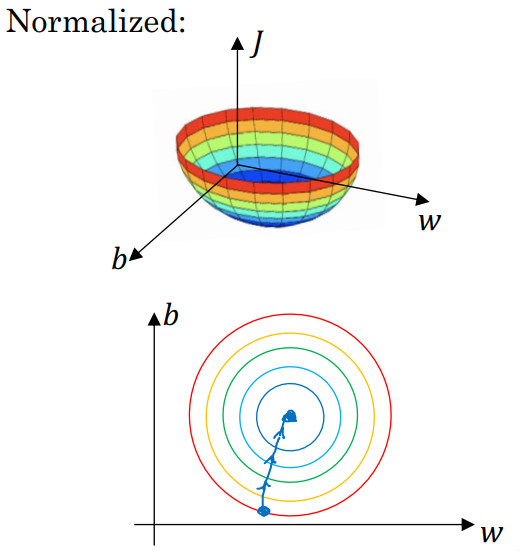

但如果函数是一个更圆的球形轮廓，那么不论从哪个位置开始，梯度下降法都能够更直接地找到最小值，你可以在梯度下降法中使用较大步长，而不需要像在左图中那样反复执行。
当然，实际上 w是一个高维向量，因此用二维绘制 w并不能正确地传达并直观理解，但总地直观理解是代价函数会更圆一些，而且更容易优化，前提是特征都在相似范围内，而不是从 1 到 1000， 0 到 1 的范围，而是在-1 到 1 范围内或相似偏差，这使得代价函数 。
所以如果输入特征处于不同范围内，可能有些特征值从 0 到 1，有些从 1 到 1000，那么归一化特征值就非常重要了。如果特征值处于相似范围内，那么归一化就不是很重要了。执行这类归一化并不会产生什么危害，我通常会做归一化处理，虽然我不确定它能否提高训练
或算法速度。