1-8 其他正则化方法

其他正则化方法（ Other regularization methods）

除了 L2正则化和随机失活（ dropout）正则化，还有几种方法可以减少神经网络中的过拟合:

数据扩增

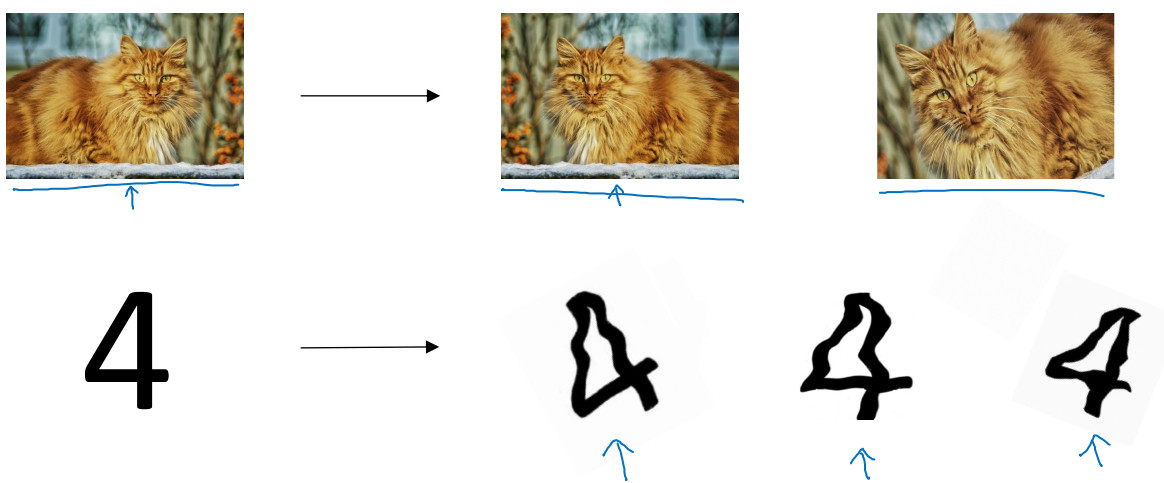
通过数据扩增可以解决过拟合问题，但是数据扩增需要付出的代价高，所以可以将原图水平翻转、随意裁剪等等手段来增加数据，对于字符可以采用扭曲的方法。

early stopping

运行梯度下降时，我们可以绘制训练误差，或只绘制代价函数 ：

因为在训练过程中，我们希望训练误差，代价函数J都在下降，通过 early stopping，我们不但可以绘制上面这些内容，还可以绘制验证集误差，它可以是验证集上的分类误差， 或验证集上的代价函数，逻辑损失和对数损失等，你会发现，验证集误差通常会先呈下降趋势，然后在某个节点处开始上升， early stopping 的作用是，你会说，神经网络已经在这个迭代过程中表现得很好了，我们在此停止训练吧，得到验证集误差 。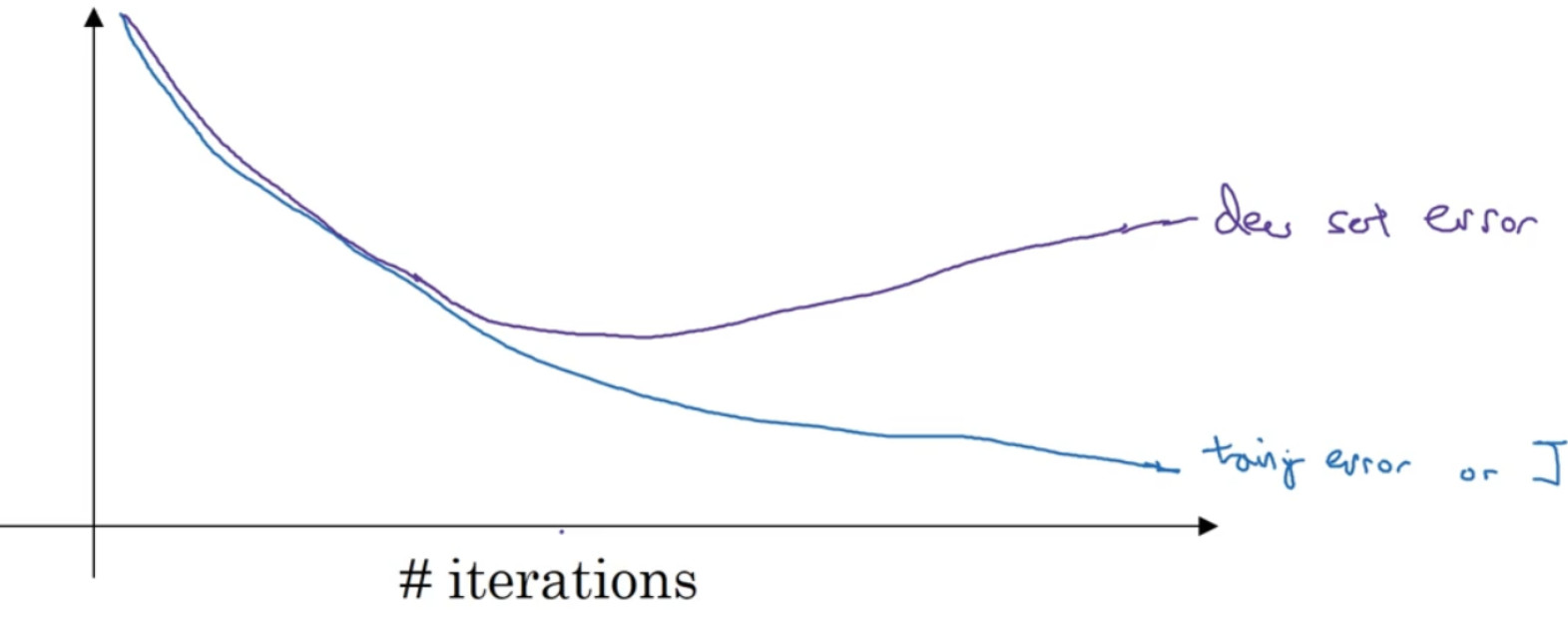


术语 early stopping 代表提早停止训练神经网络， early stopping 要做就是在中间点停止迭代过程，我们得到一个w值中等大小的弗罗贝尼乌斯范数，与 L2正则化相似，选择参数 w范数较小的神经网络 。
在机器学习中，超级参数激增，选出可行的算法也变得越来越复杂。我发现，如果我们用一组工具优化代价函数 J，机器学习就会变得更简单，在重点优化代价函数 J时，你只需要留意 w,b,$J(w,b)$的值越小越好，你只需要想办法减小这个值，其它的不用关注。然后，预防过拟合还有其他任务，换句话说就是减少方差，这一步我们用另外一套工具来实现，这个原理有时被称为“正交化”。 思路就是在一个时间做一个任务。
early stopping 的主要缺点就是你不能独立地处理这两个问题，因为提早停止梯度下降，也就是停止了优化代价函数 J，因为现在你不再尝试降低代价函数 J，所以代价函数 J的值可能不够小，同时你又希望不出现过拟合，你没有采取不同的方式来解决这两个问题，而是用一种方法同时解决两个问题，这样做的结果是我要考虑的东西变得更复杂。
如果不用 early stopping，另一种方法就是 L2正则化，训练神经网络的时间就可能很长。但是缺点在于，你必须尝试很多正则化参数 $\lambda$的值，这也导致搜索大量 $\lambda$值的计算代价太高。
Early stopping 的优点是，只运行一次梯度下降，你可以找出w较小值，中间值和较大较小值，中间值和较大值，而无需尝试L2正则化超级参数$\lambda$很多值。
虽然L2正则化有缺点，假设你可以负担大量计算的代价,还是倾向于使用此方法。