1-4 正则化

 

正则化（ Regularization）

深度学习可能存在过拟合问题——高方差，有两个解决方法：

一个是正则化；

另一个是准备更多的数据；这是非常可靠的方法，但你可能无法时时刻刻准备足够多的训练数据或者获取更多数据的成本很高。

逻辑回归中的正则化

目标：$\mathop {\min J}\limits_{w,b} (w,b)$

参数：$w \in {R^{nx}},b \in R$，w是一个多维度参数矢量，b是一个实数。

正则化项：$\frac{\lambda }{{2m}}\left\| w \right\|_2^2$

L2正则化(欧几里得2范数)：$\left\| w \right\|_2^2 = \sum\limits_{j = 1}^{nx} {w_j^2}  = {w^T}w$

L1正则化：$\frac{\lambda }{{2m}}\sum\limits_{j = 1}^{nx} {\left| {{w_j}} \right|}  = \frac{\lambda }{{2m}}{\left\| w \right\|_1}$

为什么正则化参数只有w没有b？

其实也可以将b加入到正则化当中，但因为w通常是一个高维参数矢量，已经可以表达高偏差问题，w可能还有很多的参数，我们不可能拟合所有参数，而b只是单个数字，所以w几乎涵盖所有参数，而不是b。

L1正则化

如果使用的是L1正则化，w最终会是稀疏的，也就是说w向量中会有很多0，虽然L1正则化能够使得模型变得稀疏，但是没有降低太多的存储内存，人们在训练网络时，更加倾向于使用L2正则化。 

$\lambda$是正则化参数，我们通常使用验证集或交叉验证集来配置这个参数，尝试各种各样的数据，寻找最好的参数，我们要考虑训练集之间的权衡，所以$\lambda$是另外一个需要调整的超参数。

需要注意的是$\lambda$在python中是保留字段，编写代码时，把$\lambda$写成lambd，以免与python中的保留字段冲突。 

神经网络中的正则化

 

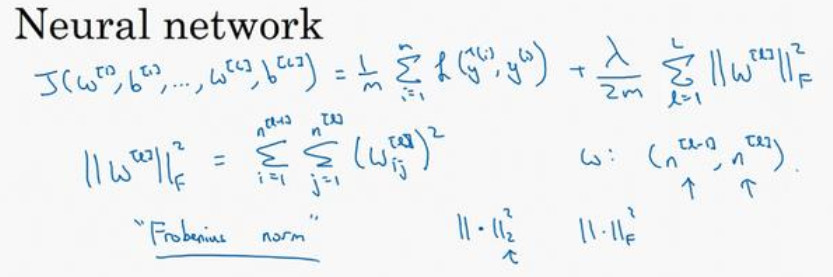
神经网络含有一个成本函数，该函数包含${{\rm{W}}^{[L]}}$, ${{\rm{b}}^{[L]}}$到 ${{\rm{W}}^{[l]}}$, ${{\rm{b}}^{[l]}}$所有参数，L表示神经网络层数，因此成本函数等于m个训练样本损失函数的总和乘以$\frac{1}{m}$，正则项为：$\frac{\lambda }{{2m}}\sum\nolimits_1^l {{{\left\| {{W^{[l]}}} \right\|}^2}} $，我们称${{{\left\| {{W^{[l]}}} \right\|}^2}}$为范数平方，这个矩阵范数${{{\left\| {{W^{[l]}}} \right\|}^2}}$(即平方范数)，被定义为矩阵中所有元素的平方和。

第一个求和符号其值从i到${n^{[l - 1]}} $，第二个值j从1到${n^{[l ]}} $，这是因为W是一个多维矩阵，其维度为：$ {n^{[l]}}*{n^{[l - 1]}}$，分别表示l层单元的数量和l-1层隐藏单元的数量。

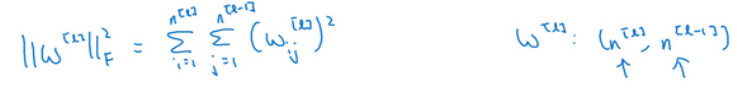
该矩阵被称为“弗罗贝尼乌斯范数”，用下标F标注，他表示一个矩阵中所有元素的平方和。

梯度下降实现

反向传播过程会计算出dW,然后更新${{\rm{W}}^{[1]}}$,现在进行参数更新时需要加上正则化项：

我们的目的是让${{\rm{W}}^{[1]}}$变得更小，实际上相当于给矩阵W乘以了$ (1 - a\frac{\lambda }{m})$倍的权重，该系数小于1，因此L2范数正则化也被称为“权重衰减”。