1-2 偏差，方差

偏差，方差（ Bias /Variance）

假设数据集：

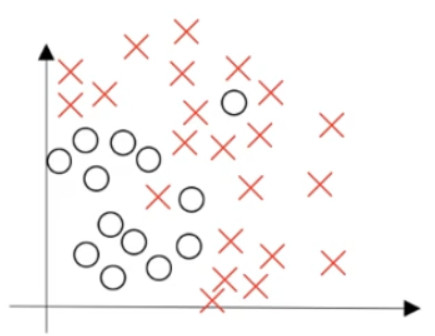
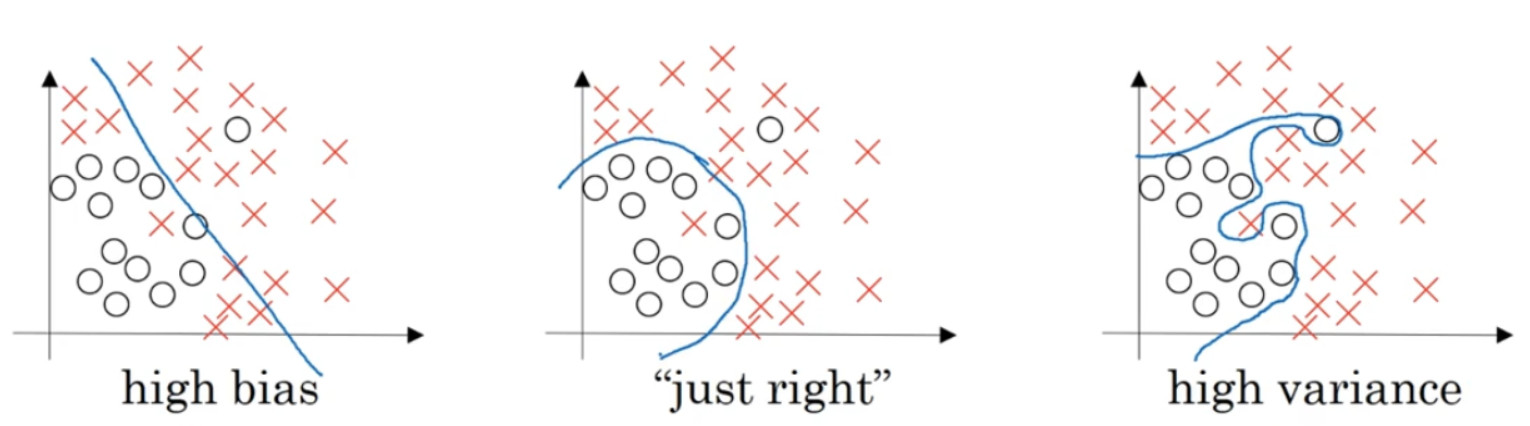
如果给这个数据集拟合一条直线，可能得到一个逻辑回归拟合，但它并不能很好地拟合该数据， 这是高偏差（ high bias）的情况， 我们称为“欠拟合（” underfitting）。

相反的如果我们拟合一个非常复杂的分类器，比如深度神经网络或含有隐藏单元的神经网络，可能就非常适用于这个数据集，但是这看起来也不是一种很好的拟合方式分类器方差较高（ high variance），数据过度拟合（ overfitting）。

在两者之间，可能还有一些像图中这样的，复杂程度适中，数据拟合适度的分类器，这个数据拟合看起来更加合理， 我们称之为“适度拟合”（ just right） 是介于过度拟合和欠拟合中间的一类。

理解偏差和方差的两个关键数据是训练集误差（ Train set error）和验证集误差（ Dev set error）：

假定训练集误差是 1%，验证集误差是 11%，可以看出训练集设置得非常好，而验证集设置相对较差， 我们可能过度拟合了训练集，在某种程度上，验证集并没有充分利用交叉验证集的作用， 像这种情况， 我们称之为“高方差”。

假设训练集误差是 15%，验证集误差是 16%，假设该案例中人的错误率几乎为 0%，人们浏览这些图片，分辨出是不是猫。算法并没有在训练集中得到很好训练，如果训练数据的拟合度不高，就是数据欠拟合，就可以说这种算法偏差比较高。相反，它对于验证集产生的结果却是合理的，验证集中的错误率只比训练集的多了 1%，所以这种算法偏差高，因为它甚至不能拟合训练集。

假设训练集误差是 15%，偏差相当高，但是，验证集的评估结果更糟糕，错误率达到 30%，在这种情况下，我会认为这种算法偏差高，因为它在训练集上结果不理想，而且方差也很高，这是方差偏差都很糟糕的情况。

假设训练集误差是 0.5%，验证集误差是 1%，用户看到这样的结果会很开心，偏差和方差都很低。

以上分析的假设条件：

这些分析都是基于假设预测的，假设人眼辨别的错误率接近 0%，一般来说，最优误差也被称为贝叶斯误差，所以，最优误差接近 0%。如果最优误差或贝叶斯误差非常高，比如 15%。我们再看看这个分类器（训练误差 15%，验证误差 16%）， 15%的错误率对训练集来说也是非常合理的，偏差不高，方差也非常低。

以上分析的前提都是假设训练集和验证集数据来自相同分布，如果没有这些假设作为前提，分析过程更加复杂。