Building your Deep Neural Network: Step by Step
作业简介
本次作业是要构建深度神经网络,通过本次作业:
- 能够使用Relu激活函数来改善你的模型
- 创建深度的神经网络(超过一个隐藏层)
- 实现易于使用的网络类
工具包
引入本次作业需要的工具包:
import numpy as np
import h5py
import matplotlib.pyplot as plt
from testCases_v2 import *
from dnn_utils_v2 import sigmoid, sigmoid_backward, relu, relu_backward
#matplotlib inline
plt.rcParams['figure.figsize'] = (5.0, 4.0) # set default size of plots
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'
#load_ext autoreloa
#autoreload 2
np.random.seed(1)
本次作业的架构
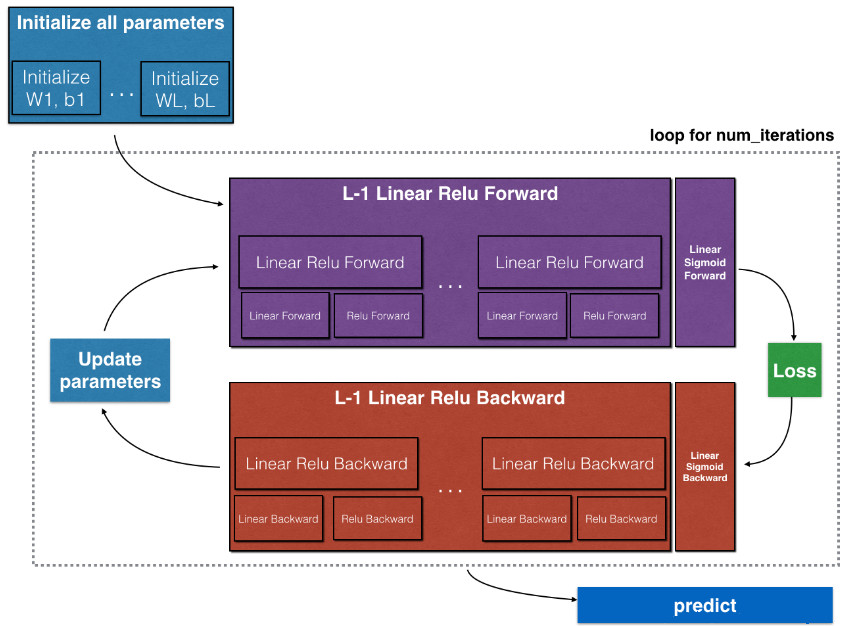
初始化两层和L层神经网络的参数
执行前向传播
- 计算前向传播的线性部分
- 使用激活函数
- 结合上述两个步骤构成一个前向传播环节
- 执行上面的前向传播环节L-1次,在最后使用Sigmoid函数。
计算损失函数
执行反向传播
- 计算反向传播中的线性部分
- 使用激活函数的导数
- 结合上述两步实现一个反向传播环节
- 执行上述反向传播环节L-1次,第L个环节使用Sigmoid
完成参数更新
需要注意的是,对于每个前向传播环节都对应于一个反向传播环节,因此,我们的每步计算都会缓存,做这些缓存的值将在计算梯度时用到。
初始化
2层神经网络
创建和初始化两层神经网络的参数:
# GRADED FUNCTION: initialize_parameters
def initialize_parameters(n_x, n_h, n_y):
np.random.seed(1)
W1 = np.random.randn(n_h, n_x) * 0.01
b1 = np.zeros((n_h, 1))
W2 = np.random.randn(n_y, n_h) * 0.01
b2 = np.zeros((n_y, 1))
assert(W1.shape == (n_h, n_x))
assert(b1.shape == (n_h, 1))
assert(W2.shape == (n_y, n_h))
assert(b2.shape == (n_y, 1))
parameters = {"W1": W1,
"b1": b1,
"W2": W2,
"b2": b2}
return parameters
测试:
parameters = initialize_parameters(2,2,1)
print("W1 = " + str(parameters["W1"]))
print("b1 = " + str(parameters["b1"]))
print("W2 = " + str(parameters["W2"]))
print("b2 = " + str(parameters["b2"]))
输出:
W1 = [[ 0.01624345 -0.00611756]
[-0.00528172 -0.01072969]]
b1 = [[ 0.]
[ 0.]]
W2 = [[ 0.00865408 -0.02301539]]
b2 = [[ 0.]]
L层神经网络
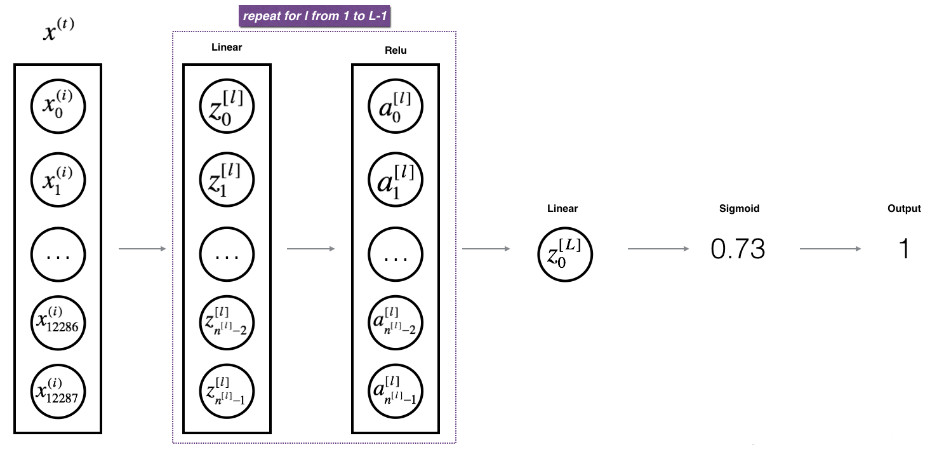
我们的输入X的维度是(12288,209),也就是说我们有209个样本,模型中各个参数的维度如下图:

再回顾一下矩阵相乘和python中的广播机制:
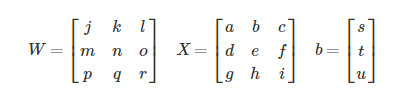
那么:
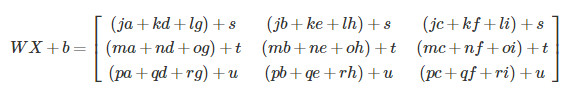
还需要注意的是模型中前L-1层都使用的是Relu激活函数,最后一层使用的是Sigmoid激活函数。
# GRADED FUNCTION: initialize_parameters_deep
def initialize_parameters_deep(layer_dims):
np.random.seed(3)
parameters = {}
L = len(layer_dims) # number of layers in the network
for l in range(1, L):
parameters['W' + str(l)] = np.random.randn(layer_dims[l], layer_dims[l-1]) * 0.01
parameters['b' + str(l)] = np.zeros((layer_dims[l], 1))
assert(parameters['W' + str(l)].shape == (layer_dims[l], layer_dims[l-1]))
assert(parameters['b' + str(l)].shape == (layer_dims[l], 1))
return parameters
测试:
parameters = initialize_parameters_deep([5,4,3])
print("W1 = " + str(parameters["W1"]))
print("b1 = " + str(parameters["b1"]))
print("W2 = " + str(parameters["W2"]))
print("b2 = " + str(parameters["b2"]))
输出:
W1 = [[ 0.01624345 -0.00611756]
[-0.00528172 -0.01072969]]
b1 = [[ 0.]
[ 0.]]
W2 = [[ 0.00865408 -0.02301539]]
b2 = [[ 0.]]
W1 = [[ 0.01788628 0.0043651 0.00096497 -0.01863493 -0.00277388]
[-0.00354759 -0.00082741 -0.00627001 -0.00043818 -0.00477218]
[-0.01313865 0.00884622 0.00881318 0.01709573 0.00050034]
[-0.00404677 -0.0054536 -0.01546477 0.00982367 -0.01101068]]
b1 = [[ 0.]
[ 0.]
[ 0.]
[ 0.]]
W2 = [[-0.01185047 -0.0020565 0.01486148 0.00236716]
[-0.01023785 -0.00712993 0.00625245 -0.00160513]
[-0.00768836 -0.00230031 0.00745056 0.01976111]]
b2 = [[ 0.]
[ 0.]
[ 0.]]
前向传播模型
线性传播
这部分可以用公式表示为:
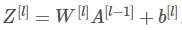
其中:
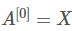
# GRADED FUNCTION: linear_forward
def linear_forward(A, W, b):
Z = np.dot(W, A) + b
assert(Z.shape == (W.shape[0], A.shape[1]))
cache = (A, W, b)
return Z, cache
测试:
A, W, b = linear_forward_test_case()
Z, linear_cache = linear_forward(A, W, b)
print("Z = " + str(Z))
输出:
Z = [[ 3.26295337 -1.23429987]]
激活函数前向传播
数学表达式为:
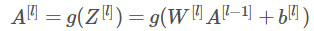
# GRADED FUNCTION: linear_activation_forward
def linear_activation_forward(A_prev, W, b, activation):
if activation == "sigmoid":
# Inputs: "A_prev, W, b". Outputs: "A, activation_cache".
Z, linear_cache = linear_forward(A_prev, W, b)
A, activation_cache = sigmoid(Z)
elif activation == "relu":
# Inputs: "A_prev, W, b". Outputs: "A, activation_cache".
Z, linear_cache = linear_forward(A_prev, W, b)
A, activation_cache = relu(Z)
assert (A.shape == (W.shape[0], A_prev.shape[1]))
cache = (linear_cache, activation_cache)
return A, cache
测试:
A_prev, W, b = linear_activation_forward_test_case()
A, linear_activation_cache = linear_activation_forward(A_prev, W, b, activation = "sigmoid")
print("With sigmoid: A = " + str(A))
A, linear_activation_cache = linear_activation_forward(A_prev, W, b, activation = "relu")
print("With ReLU: A = " + str(A))
输出:
With sigmoid: A = [[ 0.96890023 0.11013289]]
With ReLU: A = [[ 3.43896131 0. ]]
L层模型
# GRADED FUNCTION: L_model_forward
def L_model_forward(X, parameters):
caches = []
A = X
L = len(parameters) // 2 # number of layers in the neural network
# Implement [LINEAR -> RELU]*(L-1). Add "cache" to the "caches" list.
for l in range(1, L):
A_prev = A
A, cache = linear_activation_forward(A_prev, parameters["W" + str(l)], parameters["b"+str(l)], "relu")
caches.append(cache)
# Implement LINEAR -> SIGMOID. Add "cache" to the "caches" list.
AL, cache = linear_activation_forward(A, parameters["W" + str(L)], parameters["b" + str(L)], "sigmoid")
caches.append(cache)
assert(AL.shape == (1,X.shape[1]))
return AL, caches
测试:
X, parameters = L_model_forward_test_case()
AL, caches = L_model_forward(X, parameters)
print("AL = " + str(AL))
print("Length of caches list = " + str(len(caches)))
输出:
AL = [[ 0.17007265 0.2524272 ]]
Length of caches list = 2
代价函数
数学表达式:
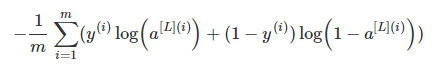
# GRADED FUNCTION: compute_cost
def compute_cost(AL, Y):
m = Y.shape[1]
# Compute loss from aL and y.
cost = -1 / m * np.sum(Y * np.log(AL) + (1-Y) * np.log(1 - AL))
cost = np.squeeze(cost) # To make sure your cost's shape is what we expect (e.g. this turns [[17]] into 17).
assert(cost.shape == ())
return cost
测试:
Y, AL = compute_cost_test_case()
print("cost = " + str(compute_cost(AL, Y)))
输出:
cost = 0.414931599615
反向传播模型
反向传播就是计算代价函数关于每个参数的导数:
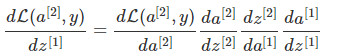
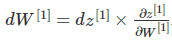
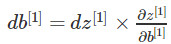
线性反向
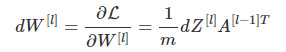
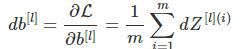
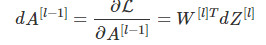
# GRADED FUNCTION: linear_backward
def linear_backward(dZ, cache):
A_prev, W, b = cache
m = A_prev.shape[1]
dW = 1 / m * np.dot(dZ, A_prev.T)
db = 1 / m * np.sum(dZ, axis=1, keepdims=True)
dA_prev = np.dot(W.T, dZ)
assert (dA_prev.shape == A_prev.shape)
assert (dW.shape == W.shape)
assert (db.shape == b.shape)
return dA_prev, dW, db
测试:
# Set up some test inputs
dZ, linear_cache = linear_backward_test_case()
dA_prev, dW, db = linear_backward(dZ, linear_cache)
print ("dA_prev = "+ str(dA_prev))
print ("dW = " + str(dW))
print ("db = " + str(db))
输出:
dA_prev = [[ 0.51822968 -0.19517421]
[-0.40506361 0.15255393]
[ 2.37496825 -0.89445391]]
dW = [[-0.10076895 1.40685096 1.64992505]]
db = [[ 0.50629448]]
线性激活反向传播
数学表达式:
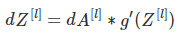
# GRADED FUNCTION: linear_activation_backward
def linear_activation_backward(dA, cache, activation):
linear_cache, activation_cache = cache
if activation == "relu":
dZ = relu_backward(dA, activation_cache)
dA_prev, dW, db = linear_backward(dZ, linear_cache)
elif activation == "sigmoid":
dZ = sigmoid_backward(dA, activation_cache)
dA_prev, dW, db = linear_backward(dZ, linear_cache)
return dA_prev, dW, db
测试:
AL, linear_activation_cache = linear_activation_backward_test_case()
dA_prev, dW, db = linear_activation_backward(AL, linear_activation_cache, activation = "sigmoid")
print ("sigmoid:")
print ("dA_prev = "+ str(dA_prev))
print ("dW = " + str(dW))
print ("db = " + str(db) + "\n")
dA_prev, dW, db = linear_activation_backward(AL, linear_activation_cache, activation = "relu")
print ("relu:")
print ("dA_prev = "+ str(dA_prev))
print ("dW = " + str(dW))
print ("db = " + str(db))
输出:
sigmoid:
dA_prev = [[ 0.11017994 0.01105339]
[ 0.09466817 0.00949723]
[-0.05743092 -0.00576154]]
dW = [[ 0.10266786 0.09778551 -0.01968084]]
db = [[-0.05729622]]
relu:
dA_prev = [[ 0.44090989 -0. ]
[ 0.37883606 -0. ]
[-0.2298228 0. ]]
dW = [[ 0.44513824 0.37371418 -0.10478989]]
db = [[-0.20837892]]
L层模型反向传播
# GRADED FUNCTION: L_model_backward
def L_model_backward(AL, Y, caches):
grads = {}
L = len(caches) # the number of layers
m = AL.shape[1]
Y = Y.reshape(AL.shape) # after this line, Y is the same shape as AL
# Initializing the backpropagation
dAL = -(np.divide(Y, AL) - np.divide((1-Y), (1-AL)))
# Lth layer (SIGMOID -> LINEAR) gradients. Inputs: "AL, Y, caches". Outputs: "grads["dAL"], grads["dWL"], grads["dbL"]
current_cache = caches[L-1]
grads["dA" + str(L)], grads["dW" + str(L)], grads["db" + str(L)] = linear_activation_backward(dAL, current_cache, "sigmoid")
for l in reversed(range(L - 1)):
# lth layer: (RELU -> LINEAR) gradients.
# Inputs: "grads["dA" + str(l + 2)], caches". Outputs: "grads["dA" + str(l + 1)] , grads["dW" + str(l + 1)] , grads["db" + str(l + 1)]
current_cache = caches[l]
dA_prev_temp, dW_temp, db_temp = linear_activation_backward(grads["dA" + str(l+2)], current_cache, "relu")
grads["dA" + str(l + 1)] = dA_prev_temp
grads["dW" + str(l + 1)] = dW_temp
grads["db" + str(l + 1)] = db_temp
return grads
测试:
AL, Y_assess, caches = L_model_backward_test_case()
grads = L_model_backward(AL, Y_assess, caches)
print ("dW1 = "+ str(grads["dW1"]))
print ("db1 = "+ str(grads["db1"]))
print ("dA1 = "+ str(grads["dA1"]))
输出:
dW1 = [[ 0.41010002 0.07807203 0.13798444 0.10502167]
[ 0. 0. 0. 0. ]
[ 0.05283652 0.01005865 0.01777766 0.0135308 ]]
db1 = [[-0.22007063]
[ 0. ]
[-0.02835349]]
dA1 = [[ 0. 0.52257901]
[ 0. -0.3269206 ]
[ 0. -0.32070404]
[ 0. -0.74079187]]
更新参数

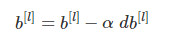
# GRADED FUNCTION: update_parameters
def update_parameters(parameters, grads, learning_rate):
L = len(parameters) // 2 # number of layers in the neural network
# Update rule for each parameter. Use a for loop.
for l in range(L):
parameters["W" + str(l+1)] = parameters["W" + str(l+1)] - learning_rate * grads["dW" + str(l+1)]
parameters["b" + str(l+1)] = parameters["b" + str(l+1)] - learning_rate * grads["db" + str(l+1)]
return parameters
测试:
parameters, grads = update_parameters_test_case()
parameters = update_parameters(parameters, grads, 0.1)
print ("W1 = "+ str(parameters["W1"]))
print ("b1 = "+ str(parameters["b1"]))
print ("W2 = "+ str(parameters["W2"]))
print ("b2 = "+ str(parameters["b2"]))
输出:
W1 = [[-0.59562069 -0.09991781 -2.14584584 1.82662008]
[-1.76569676 -0.80627147 0.51115557 -1.18258802]
[-1.0535704 -0.86128581 0.68284052 2.20374577]]
b1 = [[-0.04659241]
[-1.28888275]
[ 0.53405496]]
W2 = [[-0.55569196 0.0354055 1.32964895]]
b2 = [[-0.84610769]]


