3-2 神经网络的表示

神经网络的表示（ Neural Network Representation）

神经网络：

 

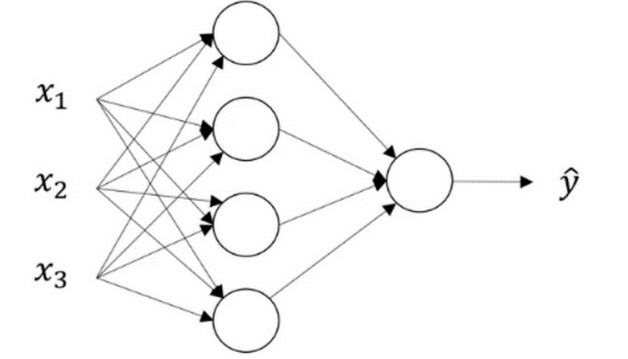
我们有输入特征x1,x2,x3它们被竖着堆叠起来，这叫做神经网络的输入层，它包含了神经网络的输入。

之后的一层称之为隐藏层。

最后一层由一个结点构成，称为输出层，它复制产生预测值。

隐藏层的含义：

　　在监督训练的神经网络中，训练集包含了输入x和输出y。所以术语隐藏层的含义是在训练集中，这些中间结点的准确值我们是不知道到的，也就是说你看不见它们在训练集中应具有的值。你能看见输入的值，你也能看见输出的值，但是隐藏层中的东西，在
训练集中你是无法看到的。所以这也解释了词语隐藏层，只是表示你无法在训练集中看到他们。
符号的含义：

$ {{\rm{a}}^{[0]}}$ 用来表示输入特征，a表示激活的意思，它意味着网络中不同层的值传递到它们后面的层中，输入层将x传递给隐藏层，所以输入层的激活值就称为$ [{{\rm{a}}^{[0]}}$，下一层即隐藏层也同样产生一些激活值，我们将其记作

$ {{\rm{a}}^{[1]}}$，对于隐藏层，第一个结点我们称为${\rm{a}}_1^{[1]}$,第二个结点我们称为${\rm{a}}_2^{[1]}$，依此类推可以表示成一个4*1的矩阵，或称为4阶列向量。我们有四个结点或者四个隐藏层单元：

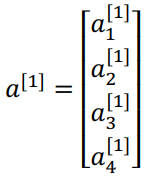
最后输出层将产生数值a，它是一个单独的实数，所得的$\hat y$将取为${a^{[2]}}$，

这个神经网络称为一个两层的神经网络：输入层并不算在总的层数内，隐藏层是第一层，输出层是第二层。输入层，我们称为第零层，所以在技术上仍然是一个三层的神经网络。

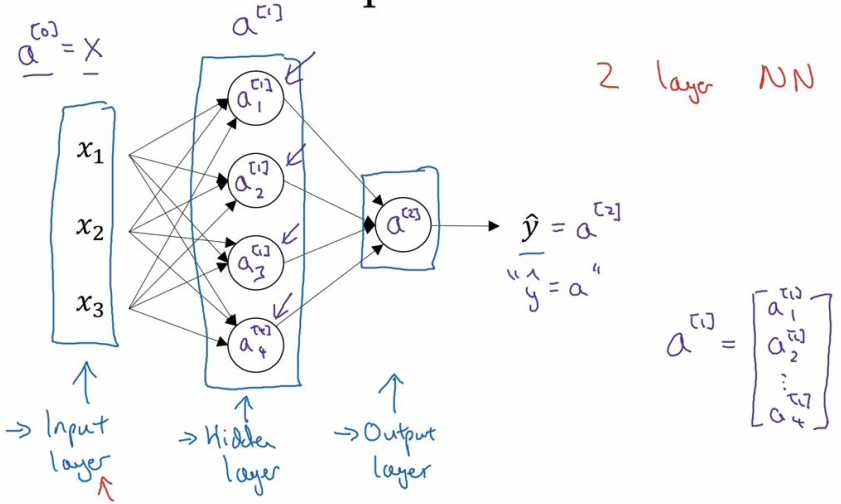
隐藏层和输出层都是带有参数的，隐藏层的参数表示为：$ ({W^{[1]}},{b^{[1]}}) $ 这里参数的维度与隐藏层的结点个数有关系，参数W是一个4*3的矩阵，参数b是一个4*1矩阵，4来源于在这里隐藏层有四个结点，3来源于输入的特征是三个。输出层的参数表示为：$ ({W^{[2]}},{b^{[2]}}) $，W的维度是1*4，b的维度是1*1,1*4是因为隐藏层有四个单元而输出层只有一个单元。