Python Basics with Numpy
Building basic functions with numpy
math.exp()
import math
def basic_sigmoid(x):
s = 1 / (1+ math.exp(-x))
return s
>>> basic_sigmoid(3)
0.9525741268224334
>>> x = [1,2,3]
>>> basic_sigmoid(x)
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
File "<stdin>", line 2, in basic_sigmoid
但是实际上在深度学习中数据往往是矩阵和向量形式,而math库函数的参数往往是一个实数,因而在深度学习中广泛使用numpy库。
numpy基础
>>> import numpy as np
>>> x = np.array([1,2,3])
>>> print(np.exp(x))
[ 2.71828183 7.3890561 20.08553692]
>>> import numpy as np
>>> x = np.array([1,2,3])
>>> print(x+3)
[4 5 6]
numpy实现sigmoid函数:
import numpy as np
def sigmoid(x):
s = 1 / (1 + np.exp(x))
return s
x = np.array([1, 2, 3])
sigmoid(x)
array([ 0.26894142, 0.11920292, 0.04742587])
求sigmoid函数的梯度
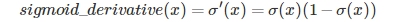
import numpy as np
def sigmoid_derivative(x):
s = 1 / (1 + np.exp(-x))
ds = s * (1-s)
return ds
x = np.array([1,2,3])
print("sigmoid_derivative(x)=" + str(sigmoid_derivative(x)))
sigmoid_derivative(x)=[ 0.19661193 0.10499359 0.04517666]
Reshaping arrays
深度学习中常用的numpy函数:np.shape,np.reshape
X.shape 用来获得矩阵或者是向量X 的维度;
X.reshape用来重新调整X的维度。
图像一般用三维矩阵表示(length,height,depth),但是,算法中往往将矩阵调整到一个向量输入,即调整成:(length*height*3,1)。
如果想将一个输入为(a,b,c)的矩阵调整到(a*b,c):
v = v.reshape((v.shape[0]*v.shape[1],v.shape[2]))
将三维图像矩阵调整为向量:
def image2vector(image):
v = image.reshape((image.shape[0]*image.shape[1]*image.shape[2],1))
return v
# This is a 3 by 3 by 2 array, typically images will be (num_px_x, num_px_y,3) where 3 represents the RGB values
image = np.array([[[ 0.67826139, 0.29380381],
[ 0.90714982, 0.52835647],
[ 0.4215251 , 0.45017551]],
[[ 0.92814219, 0.96677647],
[ 0.85304703, 0.52351845],
[ 0.19981397, 0.27417313]],
[[ 0.60659855, 0.00533165],
[ 0.10820313, 0.49978937],
[ 0.34144279, 0.94630077]]])
print ("image2vector(image) = " + str(image2vector(image)))
image2vector(image) = [[ 0.67826139]
[ 0.29380381]
[ 0.90714982]
[ 0.52835647]
[ 0.4215251 ]
[ 0.45017551]
[ 0.92814219]
[ 0.96677647]
[ 0.85304703]
[ 0.52351845]
[ 0.19981397]
[ 0.27417313]
[ 0.60659855]
[ 0.00533165]
[ 0.10820313]
[ 0.49978937]
[ 0.34144279]
[ 0.94630077]]
Normalizing rows
机器学习中常用归一化的方法来处理数据,归一化后梯度下降将会效率变高。归一化的形式例如:
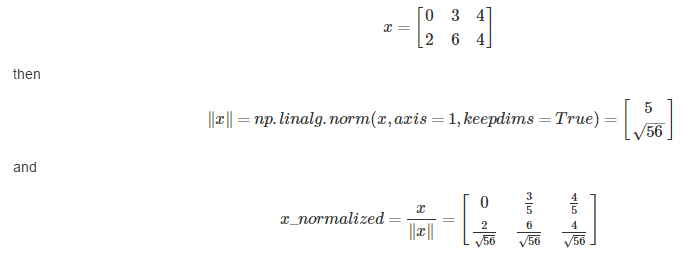
import numpy as np
def normalizeRows(x):
x_norm = np.linalg.norm(x,ord = 2,axis = 1,keepdims = True)
x = x / x_norm
return x
x = np.array([[0,3,4],[1,6,4]])
print("normalizeRows(x) = " + str(normalizeRows(x)))
normalizeRows(x) = [[ 0. 0.6 0.8 ]
[ 0.13736056 0.82416338 0.54944226]]
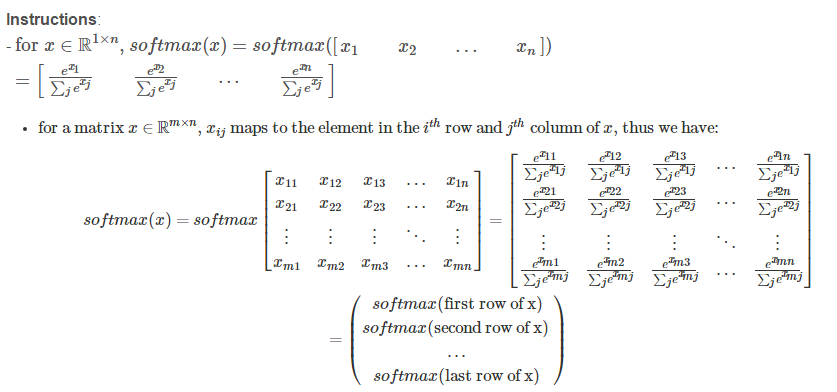
Broadcasting and the softmax function
import numpy as np
def softmax(x):
x_exp = np.exp(x)
x_sum = np.sum(x_exp,axis = 1, keepdims = True)
s = x / x_sum
return s
x = np.array([
[9, 2, 5, 0, 0],
[7, 5, 0, 0 ,0]])
print("softmax(x) = " + str(softmax(x)))
softmax(x) = [[ 0.00108947 0.0002421 0.00060526 0. 0. ]
[ 0.00560877 0.00400626 0. 0. 0. ]]
Vectorization
在深度学习中向量化是提高计算效率的有效手段。
一维向量点积运算
对于一维向量的内积运算,其结果是一个数。
非向量化一维向量内积运算:
import time
x1 = [9, 2, 5, 0, 0, 7, 5, 0, 0, 0, 9, 2, 5, 0, 0]
x2 = [9, 2, 2, 9, 0, 9, 2, 5, 0, 0, 9, 2, 5, 0, 0]
tic = time.process_time()
dot = 0
for i in range(len(x1)):
dot += x1[i] * x2[i]
toc = time.process_time()
print("dot = " + str(dot) + "\n ----- Computation time = " + str(1000 * (toc - tic)) + "ms")
向量化点积运算:
import numpy as np
import time
x1 = [9, 2, 5, 0, 0, 7, 5, 0, 0, 0, 9, 2, 5, 0, 0]
x2 = [9, 2, 2, 9, 0, 9, 2, 5, 0, 0, 9, 2, 5, 0, 0]
tic = time.process_time()
dot = np.dot(x1,x2)
toc = time.process_time()
print ("dot = " + str(dot) + "\n ----- Computation time = " + str(1000*(toc - tic)) + "ms")
outer运算
①对于多维向量,全部展开变为一维向量
②第一个参数表示倍数,使得第二个向量每次变为几倍。
③第一个参数确定结果的行,第二个参数确定结果的列
非向量化实现outer:
import numpy as np
import time
x1 = [9, 2, 5, 0, 0, 7, 5, 0, 0, 0, 9, 2, 5, 0, 0]
x2 = [9, 2, 2, 9, 0, 9, 2, 5, 0, 0, 9, 2, 5, 0, 0]
tic = time.process_time()
outer = np.zeros((len(x1),len(x2)))
for i in range(len(x1)):
for j in range(len(x2)):
outer[i,j]=x1[i]*x2[j]
toc = time.process_time()
print ("outer = " + str(outer) + "\n ----- Computation time = " + str(1000*(toc - tic)) + "ms")
向量化实现outer:
import numpy as np
import time
x1 = [9, 2, 5, 0, 0, 7, 5, 0, 0, 0, 9, 2, 5, 0, 0]
x2 = [9, 2, 2, 9, 0, 9, 2, 5, 0, 0, 9, 2, 5, 0, 0]
tic = time.process_time()
outer = np.outer(x1,x2)
toc = time.process_time()
print ("outer = " + str(outer) + "\n ----- Computation time = " + str(1000*(toc - tic)) + "ms")
对应位置元素计算
非向量化实现元素对应相乘:
import numpy as np
import time
x1 = [9, 2, 5, 0, 0, 7, 5, 0, 0, 0, 9, 2, 5, 0, 0]
x2 = [9, 2, 2, 9, 0, 9, 2, 5, 0, 0, 9, 2, 5, 0, 0]
tic = time.process_time()
mul = np.zeros((len(x1)))
for i in range(len(x1)):
mul[i]=x1[i]*x2[i]
toc = time.process_time()
print ("elementwise multiplication = " + str(mul) + "\n ----- Computation time = " + str(1000*(toc - tic)) + "ms")
向量化实现元素对应相乘:
import numpy as np
import time
x1 = [9, 2, 5, 0, 0, 7, 5, 0, 0, 0, 9, 2, 5, 0, 0]
x2 = [9, 2, 2, 9, 0, 9, 2, 5, 0, 0, 9, 2, 5, 0, 0]
tic = time.process_time()
mul = np.multiply(x1,x2)
toc = time.process_time()
print ("elementwise multiplication = " + str(mul) + "\n ----- Computation time = " + str(1000*(toc - tic)) + "ms")
矩阵相乘
非向量化的矩阵点乘:
import numpy as np
import time
x1 = [9, 2, 5, 0, 0, 7, 5, 0, 0, 0, 9, 2, 5, 0, 0]
x2 = [9, 2, 2, 9, 0, 9, 2, 5, 0, 0, 9, 2, 5, 0, 0]
W = np.random.rand(3,len(x1))
tic = time.process_time()
gdot = np.zeros(W.shape[0])
for i in range(W.shape[0]):
for j in range(len(x1)):
gdot[i] = W[i,j]*x1[j]
toc = time.process_time()
print ("gdot = " + str(gdot) + "\n ----- Computation time = " + str(1000*(toc - tic)) + "ms")
向量化的矩阵点乘:
import numpy as np
import time
x1 = [9, 2, 5, 0, 0, 7, 5, 0, 0, 0, 9, 2, 5, 0, 0]
x2 = [9, 2, 2, 9, 0, 9, 2, 5, 0, 0, 9, 2, 5, 0, 0]
W = np.random.rand(3,len(x1)) # Random 3*len(x1) numpy array
tic = time.process_time()
dot = np.dot(W,x1)
toc = time.process_time()
print ("gdot = " + str(dot) + "\n ----- Computation time = " + str(1000*(toc - tic)) + "ms")
L1、L2计算
L1计算
import numpy as np
import time
def L1(yhat,y):
loss = np.sum(np.abs(yhat-y))
return loss
yhat = np.array([.9, 0.2, 0.1, .4, .9])
y = np.array([1, 0, 0, 1, 1])
print("L1 = " + str(L1(yhat,y)))
L1 = 1.1
L2计算
import numpy as np
import time
def L2(yhat,y):
loss = np.dot((yhat-y),(yhat-y))
return loss
yhat = np.array([.9, 0.2, 0.1, .4, .9])
y = np.array([1, 0, 0, 1, 1])
print("L2 = " + str(L2(yhat,y)))
L2 = 0.43

