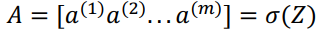2-5 向量化逻辑回归

向量化逻辑回归(Vectorizing Logistic Regression) 

前向传播过程中，

对第一个样本进行预测：${z^{(1)}} = {w^T}{x^{(1)}} + b$  $a(1) = \sigma ({z^{(1)}})$

对第二个样本进行预测：${z^{(2)}} = {w^T}{x^{(2)}} + b$  $a(2) = \sigma ({z^{(2)}})$

。。。。。。

对第m个样本进行预测：${z^{(m)}} = {w^T}{x^{(m)}} + b$  $a(m) = \sigma ({z^{(m)}})$

即，如果有m个样本，为了完成前向传播就需要进行m次这样的操作，但是采用for循环实现，效率将很低(前面已解释)，因此需要采用向量化的手段加速运算：

定义输入为矩阵X，X表示nx行m列的矩阵：

 

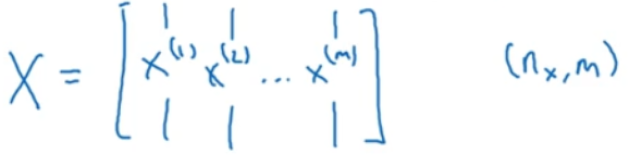
定义参数矩阵w是一个维度为nx的列向量，那么，w的装置就是一个行向量。

结果矩阵Z是一个1行m列的矩阵，可以表示为：

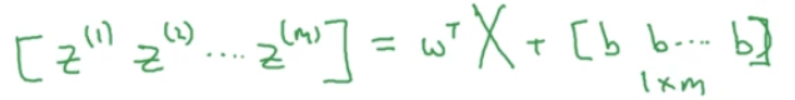
上面的计算过程，在python中可以使用一行代码表示：

Z = np.dot(w.T,X)+b

需要注意的是，这里的b是一个实数，可以说是一个1*1矩阵，但是当上面的向量加上这个实数的时候，会将b自动扩展成1*m行的行向量，这种特性在python中叫做广播(broadcasting)。

Z表示${z^{(1)}}$到${z^{(m)}}$的1*m矩阵，则同样将$[{a^{(1)}}{a^{(2)}}{a^{(3)}}...{a^{(m)}}]$表示为A。