2-3 计算图与逻辑回归中的梯度下降

计算图（ Computation Graph）

一个神经网络的计算，都是按照前向或反向传播过程组织的。首先我们计算出一个新的网络的输出（前向过程），紧接着进行一个反向传输操作。后者我们用来计算出对应的梯度或导数。

举个简单的例子，假如代价函数为J(a,b,c)=3(a+bc)，包含a，b，c三个变量。我们用u表示bc，v表示a+u，则J=3v。它的计算图可以写成如下图所示：

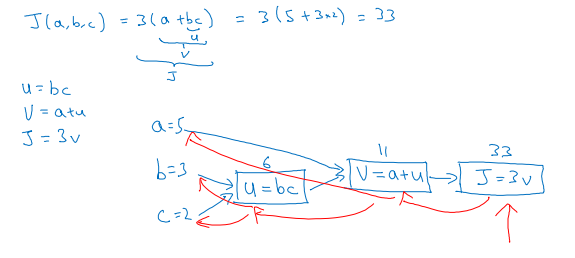
令a=5，b=3，c=2

正向传播过程：

从左到右，则u=bc=6，v=a+u=11，J=3v=33

反向传播过程：

用到的链式求导法则，求得：

$\frac{{dJ}}{{da}} = \frac{{dJ}}{{dv}}\frac{{dv}}{{da}} = 3$

$\frac{{dJ}}{{db}} = \frac{{dJ}}{{dv}}\frac{{dv}}{{du}}\frac{{du}}{{db}} = 3c$

$\frac{{dJ}}{{dc}} = \frac{{dJ}}{{dv}}\frac{{dv}}{{du}}\frac{{du}}{{dc}} = 3b$

逻辑回归中的梯度下降（ Logistic Regression Gradient Descent）

假设只有两个特征${{\rm{x}}_1}$和${{\rm{x}}_2}$,为了计算z，需要输入参数${{\rm{w}}_1}$，${{\rm{w}}_2}$和b： 

$z = {w_1}{{\rm{x}}_1} + {w_2}{x_2} + b$

$\hat y = a = \sigma (z)$

$z = {w^T}x + b$

$\sigma (z) = \frac{1}{{1 + {e^{ - z}}}}$

损失函数：

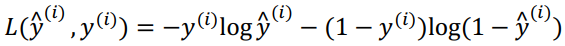
代价函数：

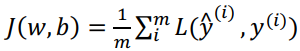
假设现在只考虑单个样本的情况，单个样本的代价函数定义如下：

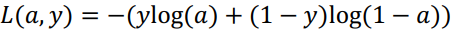
其中a是逻辑回归的输出，y是样本的标签值。

为了使得逻辑回归中最小化代价函数 L(a,y)我们仅仅需要做的就是修改参数w和b。因此需要方向计算导数：

 

从而：

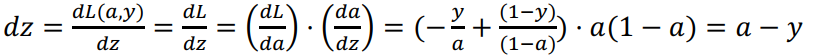
从而：

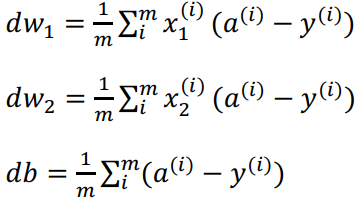
更新${w_1} = {w_1} - ad{w_1}$,更新${w_2} = {w_2} - ad{w_2}$,更新$b = b - adb$。这就是单个样本实例的梯度下降中参数更新一次的步骤。