2-2 逻辑回归代价函数与梯度下降

逻辑回归的代价函数（ Logistic Regression Cost Function） 

逻辑回归的代价函数(也称作成本函数),为了训练逻辑回归模型的参数w和参数b，需要一个代价函数。

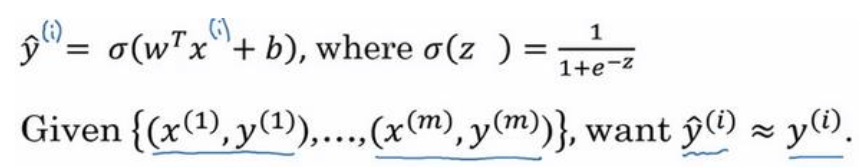
损失函数又叫做误差函数，用来衡量算法的运行情况，Loss function:$L(\hat y,y)$  

L称为的损失函数，来衡量预测输出值和实际值有多接近。一般我们用预测值和实际值的平方差或者它们平方差的一半，但是通常在逻辑回归中我们不这么做，因为当我们在学习逻辑回归参数的时候，会发现我们的优化目标不是凸优化，只能找到多个局部最优值，梯度下降法很可能找不到全局最优值。

在逻辑回归中使用的损失函数为：

 

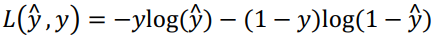
当y = 0时损失函数为：$L =  - \log (1 - \hat y)$，如果要想损失函数L尽可能得小，那么${\hat y}$就要尽可能小，因为Sigmoid函数的取值范围是[0 1]，所以${\hat y}$会无限接近于0。

当y = 1时损失函数为：$L =  - \log (\hat y)$，如果要想损失函数L尽可能得小，那么${\hat y}$就要尽可能大，因为Sigmoid函数的取值范围是[0 1]，所以${\hat y}$会无限接近于1。  

损失函数是在单个训练样本中定义的，它衡量的是算法在单个训练样本中表现如何，为了衡量算法在全部训练样本上的表现如何，我们需要定义一个算法的代价函数，算法的代价函数是对m个样本的损失函数求和除以m：

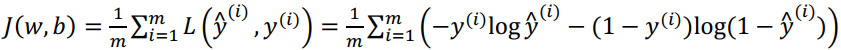
损失函数只适用于像这样的单个训练样本，而代价函数是参数的总代价，所以在训练逻辑回归模型时候，我们需要找到合适的w和b，来让代价函数J的总代价降到最低。 

梯度下降法（ Gradient Descent）

通过最小化代价函数（成本函数）$J(w,b)$来训练参数w和b。

由于$J(w,b)$是凸函数，梯度下降算法是先随机选择一组参数w和b，然后迭代的过程中分别沿着w和b的梯度的反方向前进一小步，不断修正w和b。梯度下降算法每次迭代更新，w和b的更新表达式为：

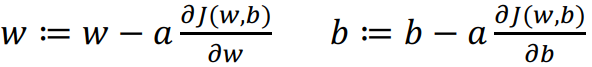
: =表示更新参数 。

a表示学习率(learning rate)，用来控制步长(step)。

$\frac{{\partial J(w,b)}}{{\partial w}}$就是函数$J(w,b)$对w求导，在代码中使用dw表示；

$\frac{{\partial J(w,b)}}{{\partial b}}$就是函数$J(w,b)$对b求导，在代码中使用db表示。

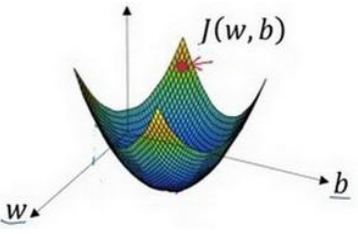
可以用如图那个小红点来初始化参数w和b，也可以采用随机初始化的方法，对于逻辑回归几乎所有的初始化方法都有效，因为函数是凸函数，无论在哪里初始化，应该达到同一点或大致相同的点。