2-1 神经网络的编程基础

二分类(Binary Classification)

二分类就是输出 y 只有离散值 { 0, 1 }。

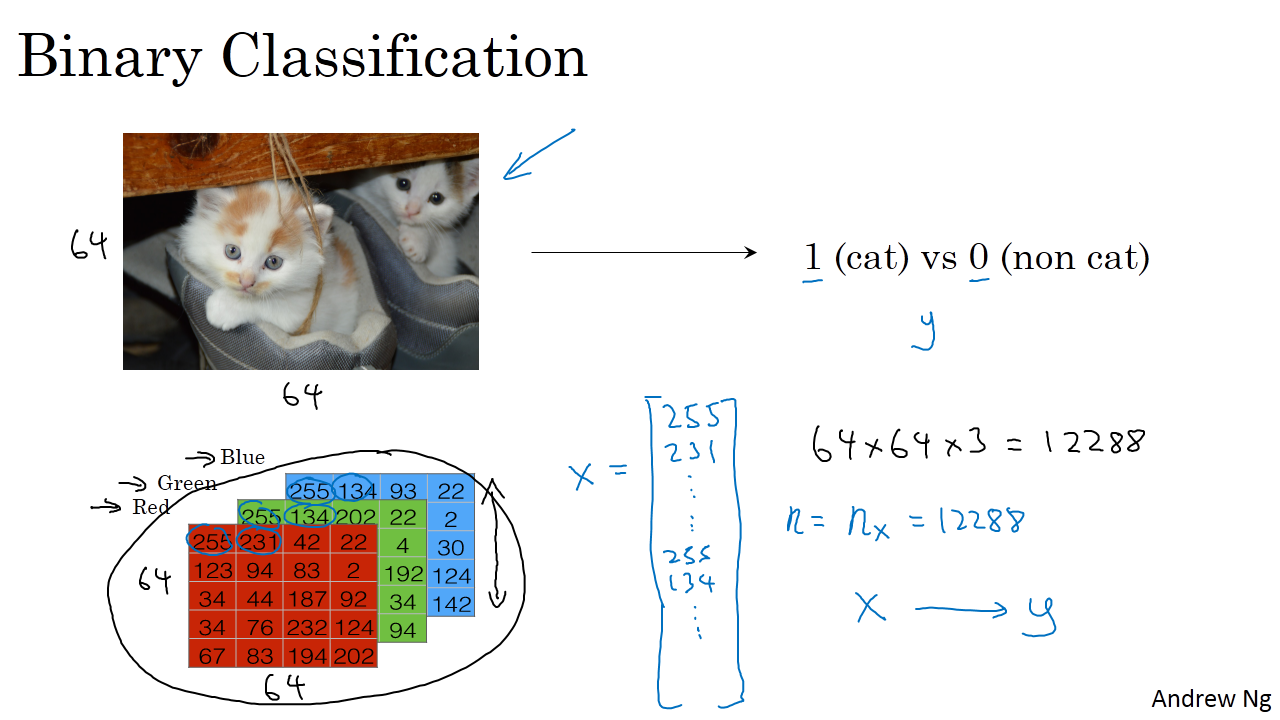
以一个图像识别问题为例，判断图片中是否有猫存在，0 代表 non cat，1 代表 cat。

一般来说，彩色图片包含RGB三个通道。我们首先要将图片输入x（维度是（64，64，3））转化为一维的特征向量。方法是每个通道逐行提取，最后连接起来，转化后的输入特征向量维度为（64x64x3=12288）。此特征向量x是列向量，维度一般记为 n_x。

符号定义 ：

 

• n：表示特征数量
• m：数据集样本个数
• x:表示一个n_x维数据，为输入数据，维度为(n_x，1)；
• y：表示输出结果，取值为(0,1)； 
• (x⁽ⁱ⁾,y⁽ⁱ⁾):表示第i组数据，可能是训练数据，也可能是测试数据； 
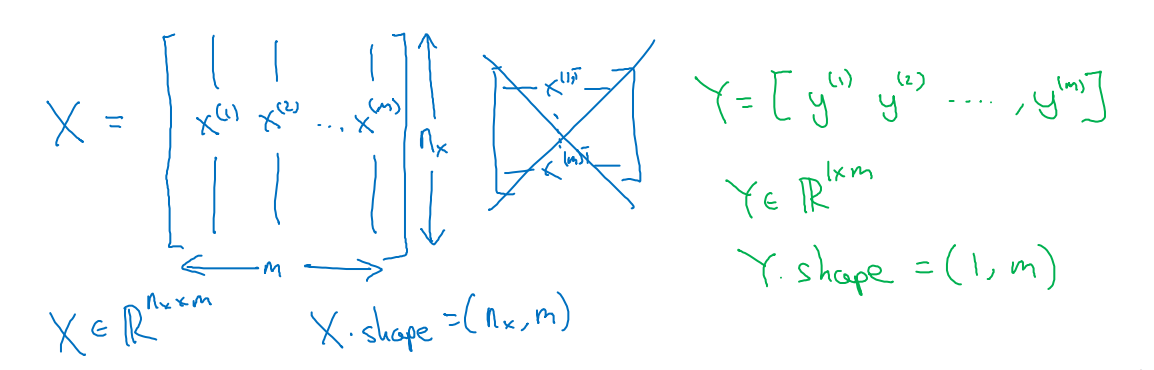
• X=[x⁽¹⁾,x⁽²⁾,x⁽³⁾,...,x^(m)]:表示所有的训练数据集的输入值，放在一个n_x*m的矩阵中;

X.shape=(n_x,m)

• Y=[y⁽¹⁾,y⁽²⁾,y⁽³⁾,...,y^(m)]:表示所有的训练数据集的输出值，维度1*m;

Y.shape=(1,m)

逻辑回归(Logistic Regression)

给定了输入特征 X，算法能够输出预测，可以记作${\rm{\hat y}}$,也就是对实际值y的估计。
用w表示逻辑回归的参数，w也是一个nx维向量(w实际上式特征权重，维度与特征向量相同)，再加上实数b作为偏差，那么${\rm{\hat y}}$可以表示为：

${\rm{\hat y}} = {{\rm{w}}^{\rm{T}}}x + b$

这时候我们得到的是一个关于输入x 的线性函数，为了使得输出的估计值范围在[01]，引入Sigmoid函数：

$y = Sigmoid({w^T}x + b) = \sigma ({w^T}x + b)$

其中Sigmoid函数为：

$\sigma (z) = \frac{1}{{1 + {e^{ - z}}}}$

注意点：

函数的一阶导数可以用其自身表示：

$\sigma (z)' = \sigma (z)(1 - \sigma (z))$ $\sigma (z)' = \sigma (z)(1 - \sigma (z))$

这里可以解释梯度消失的问题，当z0时，导数最大，但是导数最大为σ′(0)=σ(0)(1−σ(0))=0.5(1−0.5)=0.25，这里导数仅为原函数值的0.25倍。参数梯度下降公式的不断更新，σ′(z)会变得越来越小，每次迭代参数更新的步伐越来越小，最终接近于0，产生梯度消失的现象。

逻辑回归的代价函数（ Logistic Regression Cost Function）

逻辑回归的代价函数(也称作成本函数),为了训练逻辑回归模型的参数w和参数b，需要一个代价函数。

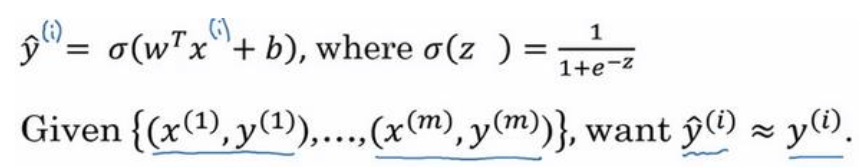
损失函数又叫做误差函数，用来衡量算法的运行情况，Loss function:$L(\hat y,y)$ 

L称为的损失函数，来衡量预测输出值和实际值有多接近。一般我们用预测值和实际值的平方差或者它们平方差的一半，但是通常在逻辑回归中我们不这么做，因为当我们在学习逻辑回归参数的时候，会发现我们的优化目标不是凸优化，只能找到多个局部最优值，梯度下降法很可能找不到全局最优值。

在逻辑回归中使用的损失函数为：

$L(\hat y,y) =  - y\log (\hat y) - (1 - y)\log (1 - \hat y)$  $L(\hat y,y) =  - y\log (\hat y) - (1 - y)\log (1 - \hat y)$ 

当y = 1时损失函数为：$L =  - \log (\hat y)$，如果要想损失函数L尽可能得小，那么${\hat y}$就要尽可能大，因为Sigmoid函数的取值范围是[0 1]，所以${\hat y}$会无限接近于1。 

当y = 0时损失函数为：$L =  - \log (1 - \hat y)$，如果要想损失函数L尽可能得小，那么${\hat y}$就要尽可能小，因为Sigmoid函数的取值范围是[0 1]，所以${\hat y}$会无限接近于0。

损失函数是在单个训练样本中定义的，它衡量的是算法在单个训练样本中表现如何，为了衡量算法在全部训练样本上的表现如何，我们需要定义一个算法的代价函数，算法的代价函数是对m个样本的损失函数求和除以m：

$J(w,b) = \frac{1}{m}\sum\nolimits_{i = 1}^m {L({{\hat y}^{(i)}},{y^{(i)}})}  = \frac{1}{m}\sum\nolimits_{i = 1}^m {( - {y^{(i)}}\log {{\hat y}^{(i)}} - (1 - {y^{(i)}})\log (1 - {{\hat y}^{(i)}})} )$ 

损失函数只适用于像这样的单个训练样本，而代价函数是参数的总代价，所以在训练逻辑回归模型时候，我们需要找到合适的w和b，来让代价函数J的总代价降到最低。