递归函数

C通过运行时堆栈支持递归函数的实现，递归函数就是直接或者间接调用自身的函数。

递归函数追踪

追踪递归函数执行过程的关键是理解函数中所声明的变量是如何存储的：当函数被调用时，它的变量的空间创建于运行时堆栈上，以前调用的函数的变量扔保留在堆栈上，但它们被新函数的变量所覆盖，因此不能被访问。

递归函数每进行一次新的调用，都将创建一批新的变量，它们将掩盖函数前一次调用所创建的变量，当我们追踪一个递归函数的执行过程时，必须把分属不同次调用的变量区分开，以免混淆。

例如： 

#include<stdio.h>
void binary_to_ascii(unsigned int value)
{
  unsigned int quotient;
  quotient=value/10;
  if(quo!=0)
    binary_to_ascii(quotient);
  putchar(value+'0');  putchar('\n');  printf("value=%d\n",value);
}

main(){
unsigned int a=4267;
binary_to_ascii(a);
}

 当函数开始执行时，堆栈的内容如下图所示：

执行除法运算之后，堆栈的内容：

 接着，if语句判断出quotient的值非零，所以对该函数执行递归调用，当函数第二次被调用之初，堆栈的内容：

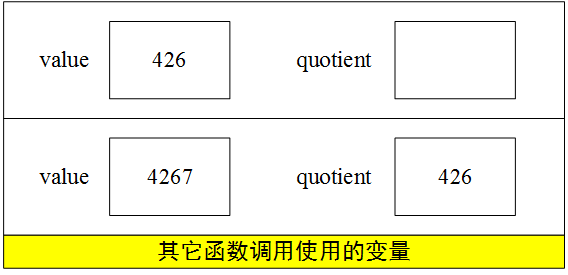
 堆栈上创建了一新的变量，隐藏了前面那批变量，除非当前这次调用返回，否则它们是不能被访问的，在此执行除法后堆栈的内容：

 

quotient的值是42，非零，所以继续执行递归调用，并再创建一批变量，再次执行完除法之后，堆栈的内容：

 quotient的值是4，非零，所以继续执行递归调用，并再创建一批变量，再次执行完除法之后，堆栈的内容：

 

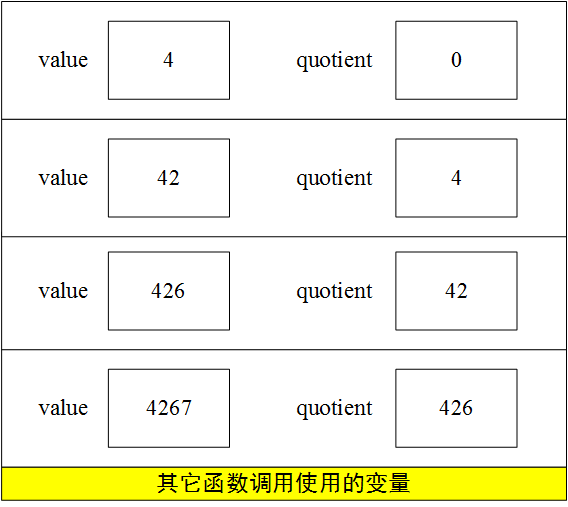
 现在，quotient的值是0了，不再调用递归循环，开始打印输出，然后函数返回，并开始销毁堆栈上的变量值。

每次调用putchar得到Value的最后一个数字，经过并将字符转换成ASCII码，并打印：

 接着函数返回，它的变量从堆栈中销毁。接着，递归函数前一次调用重新继续执行，它所使用的是自己的变量，它们现在位于堆栈的顶端，所以调用putchar后打印出来的数字是2。

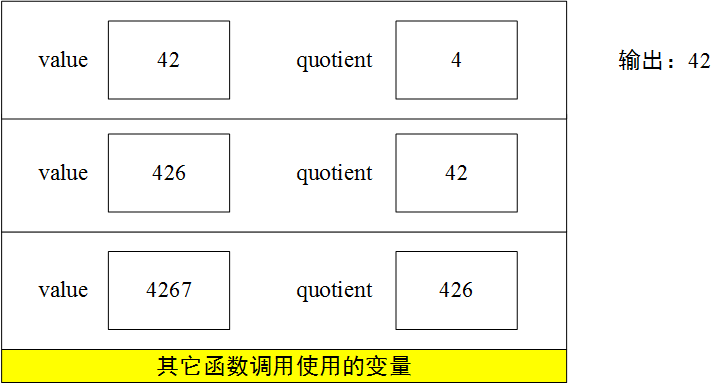
 接着函数返回，它的变量从堆栈中销毁。接着，递归函数前一次调用重新继续执行，它所使用的是自己的变量，它们现在位于堆栈的顶端，所以调用putchar后打印出来的数字是6。

接着函数返回，它的变量从堆栈中销毁。接着，递归函数前一次调用重新继续执行，它所使用的是自己的变量，它们现在位于堆栈的顶端，所以调用putchar后打印出来的数字是7。

递归函数与迭代

1.计算n的阶乘：

递归实现n的阶乘

long  factorial(int n)
{
        if (0 >= n) {
              return  1;
        } else {
             return  n*factorial(n-1);  //尾部递归可以方便得转换为迭代实现
        }
}

迭代实现n的阶乘

long  factorial(int  n)
{
        int     result = 1;
        while (1 < n) {
                result *= n;
                n -= 1;
        }
        return  result;
}

对比：在计算n的阶乘的两种方法中，递归并没有体现出它的优势，因为递归函数调用将涉及到运行时开销，比如参数入栈，为局部变量分配内存空间，保存寄存器的值，在函数返回时，参数出栈，销毁局部变量，寄存器恢复。这样的话，用迭代效率更高一些。

 2.计算斐波那契数

斐波那契数其实是一个数列，它的每个数的数值是前两个数之和，第一个和第二个数为1。

斐波那契数的递归实现，计算第n个斐波那契数：

long  fibonacci(int  n)
{
          if (2 >= n) {
                 return 1;
         } else {
                 return   (fibonacci(n-1) + fibonacci(n-2)) //尾部递归可以用迭代实现
         }
}

斐波那契数的迭代实现，计算第n个斐波那契数：

long  fibonacci(int  n)
{
        long     result;
        long      prev; //前面的那个数
        long     next; // 前面的第二个数
        
        result = 1;
        prev = 1;

       while (2 < n) {
　　　　　　　　next = prev;
              prev = result;
              result = prev + next;
             n--;
     }
     return result;
}

对比：在递归版本中存在冗余计算，效率相当低；应采用第二种方法。