DQN（Deep Q-learning）入门教程（三）之蒙特卡罗法算法与Q-learning算法

蒙特卡罗法

在介绍Q-learing算法之前，我们还是对蒙特卡罗法（MC）进行一些介绍。MC方法是一种无模型（model-free）的强化学习方法，目标是得到最优的行为价值函数$q_*$。在前面一篇博客中，我们所介绍的动态规划算法则是一种有模型的算法。那么问题来了，什么是模型（model）？模型其实就是我们在第一篇博客：DQN（Deep Q-learning）入门教程（一）之强化学习介绍种所介绍的状态转化模型： $P_{ss'}^a$。

在动态规划解决问题的时候，我们是已知$P_{ss'}^a$，但是实际上我们也可能对于$P_{ss'}^a$我们是未知的。那么怎么办呢？此时，我们使用经验平均来解决这个问题。其中的思想有点类似大数定理，尽管我不知道模型概率是什么，但是我可以使用无数次的实验来逼近这个概率。

任然是分为两个部分：

1. 策略评估
2. 策略控制
   • 探索性
   • 无探索性

策略评估

前面我们说了，我们使用多次实验来解决model-free，因此我们将历史实验数据称之为经验，然后进行平均求得的价值函数当成价值函数当作结果。

• 经验：我们使用策略做很多次实验，每次实验都是从最初状态到终止状态。假如一次实验所得得到的数据如下：$S_1,A_1,R_2,S_2,A_2,...S_t,A_t,R_{t+1},...R_T, S_T$，则在状态$s$处获得的回报是：$G_{t}(s)=R_{t+1}+\gamma R_{t+2}+\cdots+\gamma^{T-1} R_{T}$。而我们就可以进行多次实验，就可以得到多份数据。

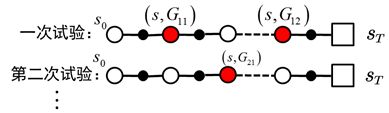
• 平均：平均有两种方式，第一次访问蒙特卡罗方法和每次访问蒙特卡罗方法。假如我们做实验的到的数据如下，现在需要来计算$G(s)$:

  

  1. 第一次访问蒙特卡罗方法：只是使用每次实验第一次出现状态$s$的放回值。比如说上图中$G_{11},G_{21}$，但是不使用$G_{12}$。

     $$\begin{equation}v(s)=\frac{G_{11}(s)+G_{21}(s)+\cdots}{N(s)}\end{equation} \\ N(s)代表出现的次数$$

  2. 每次访问蒙特卡罗方法：则就是只要出现过，就使用，比如说上图中的$G_{11},G_{12},G_{21}$。

     $$\begin{equation}v(s)=\frac{G_{11}(s)+G_{12}(s)+\cdots+G_{21}(s)+\cdots}{N(s)}\end{equation}$$

不过我们可以想一想，这样计算平均值会有什么问题？浪费内存空间，因为我们需要储存该状态所有历史实验数据然后再取平均。因此我们对取平均值的方法进行改进，改进的原理如下：

$$\begin{equation}\mu_{k}=\frac{1}{k} \sum_{j=1}^{k} x_{j}=\frac{1}{k}\left(x_{k}+\sum_{j=1}^{k-1} x_{j}\right)=\frac{1}{k}\left(x_{k}+(k-1) \mu_{k-1}\right)=\mu_{k-1}+\frac{1}{k}\left(x_{k}-\mu_{k-1}\right)\end{equation}$$

也就是说，状态价值公式可以改写为：

$$\begin{equation}\begin{array}{c} N\left(s\right)=N\left(s\right)+1 \\ V_{k+1}\left(s\right)=V_{k}\left(S\right)+\frac{1}{N\left(S\right)}\left(G_{t}-V_{k}\left(S\right)\right) \end{array}\end{equation}$$

这样我们存储上一步的状态价值函数就🆗了。若$N(s)$越大，则$\frac{1}{N(s)}$越小，则新样本对总体均值的影响小，反之亦然。实际上，我们也可以使用一个学习率$\alpha$代替$V\left(s\right)=V\left(S\right)+\alpha\left(G_{t}-V\left(S\right)\right)$。

探索性初始化MC控制

探索性初始是指每个状态都有一定几率作为初始状态。因此这里有一个前提就是对于所有的状态我们都是已知的，这样我们才能够从状态集中随机的选取$s \in \mathcal{S}$。

算法的流程图如下：

无探索性初始化MC控制

ES的方法有一点问题，因为有时候agent是不可能在任意状态开始的，比如说你玩电游，初始状态是确定的，只有一个或者几个，ES方法是一个不现实的假设，同时我们也不知道所有的状态集$\mathcal{S}$。

无探索性初始是指初始状态是固定的，然后我们在里面加入探索率 $\epsilon$ （随着试验次数的增加而逐渐减小）来对$action$选择：使用$1 - \epsilon$的概率贪婪地选择目前认为是最大行为价值的行为，而使用 $\epsilon$的概率随机的从所有$m$ 个可选的行为中随机选择行为。该方法称之为$\epsilon-greedy$

用公式可以表示为：

$$\pi(a|s)= \begin{cases} \epsilon/m + 1- \epsilon & {if\; a_{*} = \arg\max_{a \in A}Q(s,a)}\\ \epsilon/m & {else} \end{cases}$$

而方法又可以分为两种：

• On-Policy：直接对我们的策略进行估值和改进
• Off-Policy：结合一个其他的策略，来对我们的决策策略进行估值和改进。

On-Policy的算法如下所示：

输入：状态集 $S,$ 动作集 $A,$ 即时奖励 $R,$ 哀減因子 $\gamma,$ 探索率 $\epsilon$
输出：最优的动作价值函数 $q_{*}$ 和最优策略 $\pi_{*}$

1. 初始化所有的动作价值Q $(s, a)=0,$ 状态次数 $N(s, a)=0,$ 采样次数 $k=0,$ 随机初始化一个策略 $\pi$

2. $k=k+1$, 基于策略 $\pi$ 进行第k次蒙特卡罗采样，得到一个完整的状态序列：

$$S_{1}, A_{1}, R_{2}, S_{2}, A_{2}, \ldots S_{t}, A_{t}, R_{t+1}, \ldots R_{T}, S_{T}$$

3. 对于该状态序列里出现的每一状态行为对 $\left(S_{t}, A_{t}\right),$ 计算其收获 $G_{t},$ 更新其计数 $N(s, a)$ 和行为价值函数 $Q(s, a)$

$$\begin{array}{c} G_{t}=R_{t+1}+\gamma R_{t+2}+\gamma^{2} R_{t+3}+\ldots \gamma^{T-t-1} R_{T} \\ N\left(S_{t}, A_{t}\right)=N\left(S_{t}, A_{t}\right)+1 \\ Q\left(S_{t}, A_{t}\right)=Q\left(S_{t}, A_{t}\right)+\frac{1}{N\left(S_{t}, A_{t}\right)}\left(G_{t}-Q\left(S_{t}, A_{t}\right)\right) \end{array}$$

4. 基于新计算出的动作价值, 更新当前的 $\epsilon-贪婪$策略:

$$\epsilon=\frac{1}{k}$$

$$\pi(a | s)=\left\{\begin{array}{ll} \epsilon / m+1-\epsilon & \text { if } a^{*}=\arg \max _{a \in A} Q(s, a) \\ \epsilon / m & \text { else } \end{array}\right.$$

5. 如果所有的Q $(s, a)$ 收敛, 则对应的所有 $Q(s, a)$ 即为最优的动作价值函数 $q_{* \circ}$ 对应的策略 $\pi(a | s)$ 即为最优策略 $\pi_{* \circ}$ 否则转到第二步。

Off-Policy的介绍可以看这里

蒙特卡罗方法解决了状态转移模型$P$未知的问题，但是其有一个特点，算法需要一个完整的$episode$才能够进行策略更新。

Q-learning简介

下面是维基百科上面关于Q-learning的介绍。

Q-learning is a model-free reinforcement learning algorithm to learn a policy telling an agent what action to take under what circumstances. It does not require a model (hence the connotation "model-free") of the environment, and it can handle problems with stochastic transitions and rewards, without requiring adaptations.

Q-learning和MC方法都是model-free的方法。与MC方法类似的是，它两都是使用价值迭代来更新价值函数，最后更新策略。不过与MC方法不同的是：MC方法需要完整的$episode$才能进行更新，而Q-learning则不需要。

Q说明

首先先说一下Q-learning 中的Q，Q代表这动作价值函数$q(a,s)$，Q的更新公式如下：

$${\displaystyle Q^{new}(s_{t},a_{t})\leftarrow \underbrace {Q(s_{t},a_{t})} _{\text{旧的值}}+\underbrace {\alpha } _{\text{学习率}}\cdot \overbrace {{\bigg (}\underbrace {\underbrace {r_{t}} _{\text{奖励}}+\underbrace {\gamma } _{\text{奖励衰减因子}}\cdot \underbrace {\max _{a}Q(s_{t+1},a)} _{\text{estimate of optimal future value}}} _{\text{new value (temporal difference target)}}-\underbrace {Q(s_{t},a_{t})} _{\text{旧的值}}{\bigg )}} ^{\text{temporal difference}}}$$

这里借助莫烦教程里面的一些图来进行说明：

• Q现实：表示我们执行Action得到的动作价值
• Q估计：表示这个值是由我们进行迭代估计的

算法步骤

算法的步骤如下：

算法输入：迭代轮数T，状态集S, 动作集 $A,$ 步长 $\alpha,$ 哀減因子 $\gamma,$ 探索率 $\epsilon$
输出：所有的状态和动作对应的价值 $Q$

1. 随机初始化所有的状态和动作对应的价值Q，对于终止状态其Q值初始化为0.

2. for i in range(0,T), 进行迭代：
   a) 初始化S为当前状态序列的第一个状态。
   b) 用$\epsilon-贪婪法$在当前状态$S$选择出动作 $A$
   c) 在状态$S$执行当前动作 $A,$ 得到新状态 $S^{\prime}$ 和奖励 $R$
   d) 更新价值函数:$Q(S, A)+\alpha\left(R+\gamma \max _{a} Q\left(S^{\prime}, a\right)-Q(S, A)\right)$
   e) $S=S^{\prime}$
   f) 如果S'是终止状态, 当前轮迭代完毕，否则转到步骤b

总结

这篇博客主要是介绍了无模型下的问题求解方式：蒙特卡罗法和Q-learning法。在下篇博客中，将使用q-learning算法具体进行实践。

参考

• Q-learning
• Monte Carlo in Reinforcement Learning, the Easy Way
• [https://people.cs.umass.edu/_{barto/courses/cs687/Chapter%205.pdf](https://people.cs.umass.edu/}barto/courses/cs687/Chapter 5.pdf)
• 什么是 Q Leaning
• 强化学习（七）时序差分离线控制算法Q-Learning
• 强化学习（四）用蒙特卡罗法（MC）求解