DQN（Deep Q-learning）入门教程（二）之最优选择

在上一篇博客：DQN（Deep Q-learning）入门教程（一）之强化学习介绍中有三个很重要的函数：

• 策略：\(\pi(a|s) = P(A_t=a | S_t=s)\)

• 状态价值函数：\(v_\pi(s)=\mathbb{E}\left[R_{t+1}+\gamma \left(S_{t+1}\right) | S_{t}=s\right]\)

• 动作价值函数：\(q_{\pi}(s,a) = \mathbb{E}_{\pi}(R_{t+1} + \gamma q_{\pi}(S_{t+1},A_{t+1}) | S_t=s, A_t=a)\)

两个价值函数分别代表了某个状态的价值，和在状态\(s_t\)下做某个action的价值。而策略函数就是我们需要进行求解的。因为对于我们来说，肯定是希望某个策略能够得到最大的价值。比如说，你会选择努力学习而不是去网吧，以获得棒棒糖的奖励。

一般来说，比较难去找到一个最优策略，但是可以通过比较若干不同策略的优劣来确定一个较好的策略，也就是局部最优解。

​ ——强化学习（二）马尔科夫决策过程(MDP)

最优策略

首先，我们知道“好的策略产生好的价值”，因此策略的好坏可以通过价值的大小来比较。我们定义最佳的策略是 \(\pi_*\) ,而我们的目的就是为了寻找这个 \(\pi_*\)

1. 最优状态价值函数：代表所有策略下产生的不同状态的状态的价值函数中的最大值。

   \[v_{*}(s) = \max_{\pi}v_{\pi}(s) \]

2. 最优动作价值函数：代表所有策略下产生众多动作价值函数中的最大值。

   \[q_{*}(s,a) = \max_{\pi}q_{\pi}(s,a) \]

   怎么理解这个最优动作（行为）价值函数呢？个人觉得（如果有错的话，欢迎在评论区留言告诉我）

应该是这样的：

目前我们有一个最好的策略 \(\pi_*\)，它一定能够保证我们获得最好的分数。我们在\(t\)时刻执行的动作是\(a\)，然后在接下来的时刻，执行的策略都是 \(\pi_*\) ，因此\(q_*(s,a)\) 一定是在当前状态\(s\)下能够执行\(a\)能够获得最好的分数了。那么，他有什么含义呢？它可以代表在当前状态执行\(a\) 动作好不好。比如说\(q_*(s,a_1) > q_*(s,a_2)\) 则就代表\(a_1\)比\(a_2\)好，因为它能够获得更多的奖励分数。

1. 两个之间的关系：

结合下图，我们可以知道：

\[v_{*}(s) = \max_{\pi}v_{\pi}(s) = \max_{a}q_{*}(s,a) \\ q_{*}(s,a) = \max_{\pi}q_{\pi}(s,a) = R_s^a + \gamma \sum\limits_{s' \in S}P_{ss'}^av_{*}(s') \]

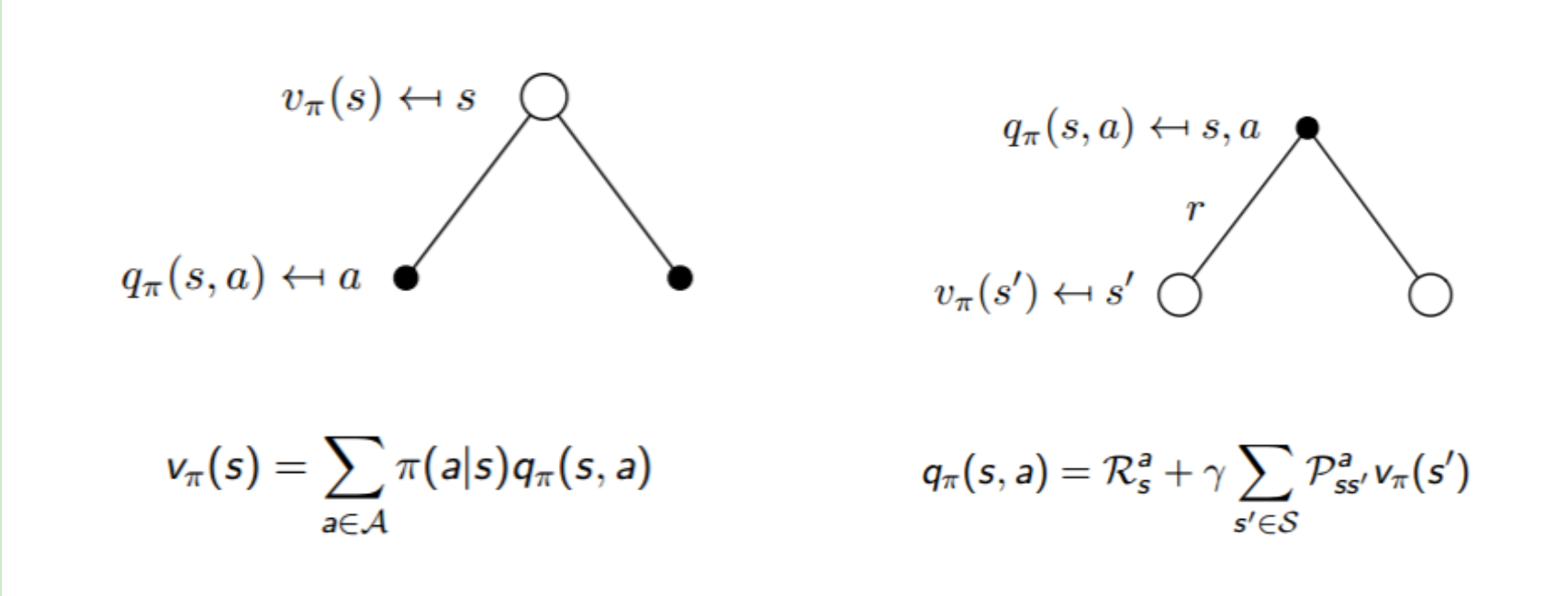
实际上，寻找最优策略的过程就是寻找最优动作的过程：选取一个\(a\)使得\(q_{\pi}(s,a)\)最大。针对于最优策略，基于动作价值函数我们可以定义为：

\[\pi_{*}(a|s)= \begin{cases} 1 & {if\;a=\arg\max_{a \in A}q_{*}(s,a)}\\ 0 & {else} \end{cases} \]

最优策略实例

下图是UCL强化强化学习课程的一个实例，黄色圆圈的开始状态，红色方块的是结束状态。\(R\)代表reward，每一个状态可以执行的action为红色字体（例如Facebook，Study等等），其中黑色的点分支对应的数字代表执行这个action之后的状态转移概率。

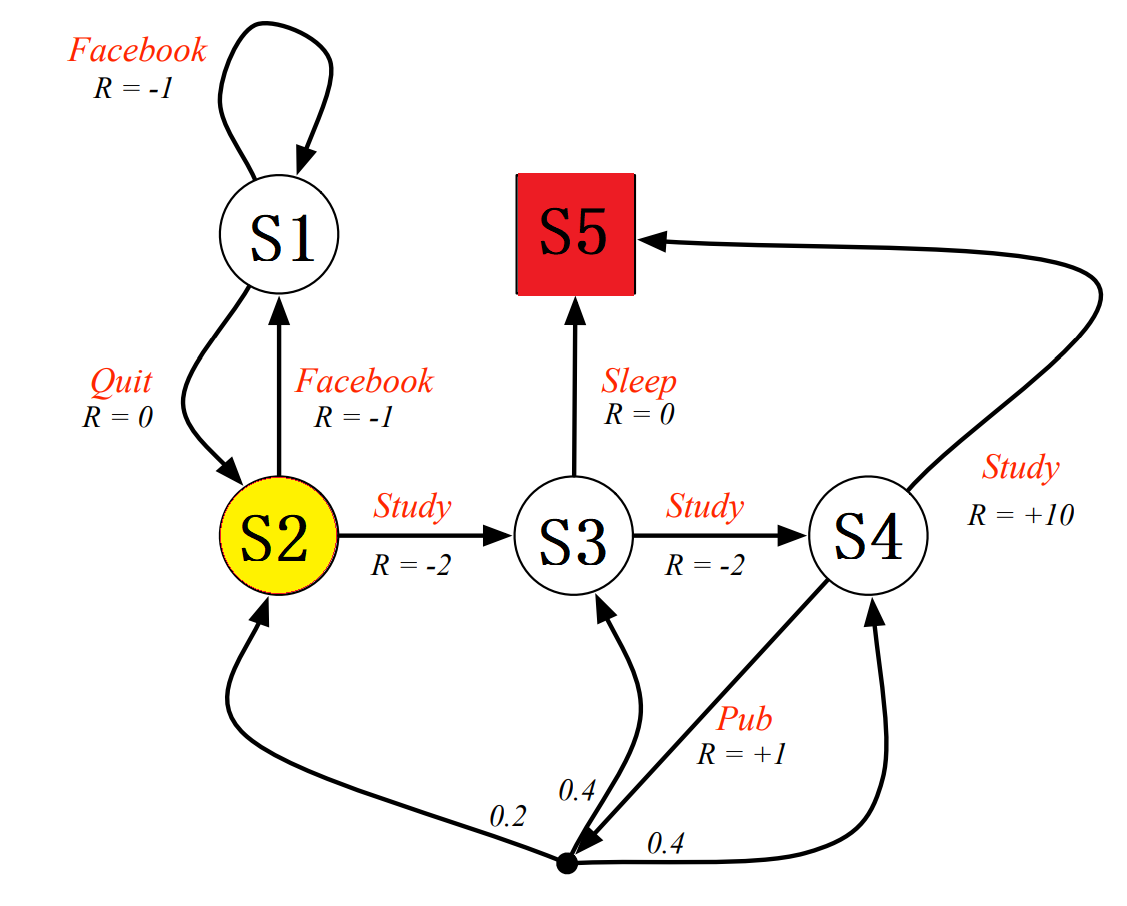
我们设衰减因子：\(\gamma = 1\)，因为每一个state都只对应2个action，因此，我们设初始策略\(\pi(a|s) = 0.5\)。其终点（也就是\(s_5\)）没有下一个状态，同时也没有相应的动作，因为我们定义其价值为\(v_5 =0\)。

这里复说一下状态价值函数的定义：\(v_{\pi}(s) = \sum\limits_{a \in A} \pi(a|s)(R_s^a + \gamma \sum\limits_{s' \in S}P_{ss'}^av_{\pi}(s'))\)

1. 针对于\(v_1\)：\(v_1 = 0.5*(-1+v_1) +0.5*(0+v_2)\)
2. 针对于\(v_2\)：\(v_2 = 0.5*(-1+v_1) +0.5*(-2+v_3)\)
3. 针对于\(v_3\)：\(v_3 = 0.5*(-2+v_4) +0.5*(0+v_5)\)
4. 针对于\(v_4\)：\(v_4 = 0.5*(10+v_5) +0.5*(1+0.2*v_2+0.4*v_3+0.4*v_4)\)

解得方程组为:\(v_1=-2.3, v_2=-1.3, v_3=2.7, v_4=7.4\)。

上面是我们固定了策略\(\pi(a,s) = 0.5\)得到得每一个状态得价值函数，因此上面的到的\(v\)很可能不是最大的价值函数，因为这个策略不是最好的策略。

寻求最佳策略就是寻找最佳得动作价值函数，因此我们如果能够得到最优动作价值函数，也就得到了策略 \(\pi_*\) 。

还是以上面得那个例子为例，通过求解每一个action对应得\(q_*(s,a)\)。然后就可以得到最优策略。（策略即为\(s_2 \rarr s_3 \rarr s_4 \rarr s_5\)）

下图中的9.4应该为8.4

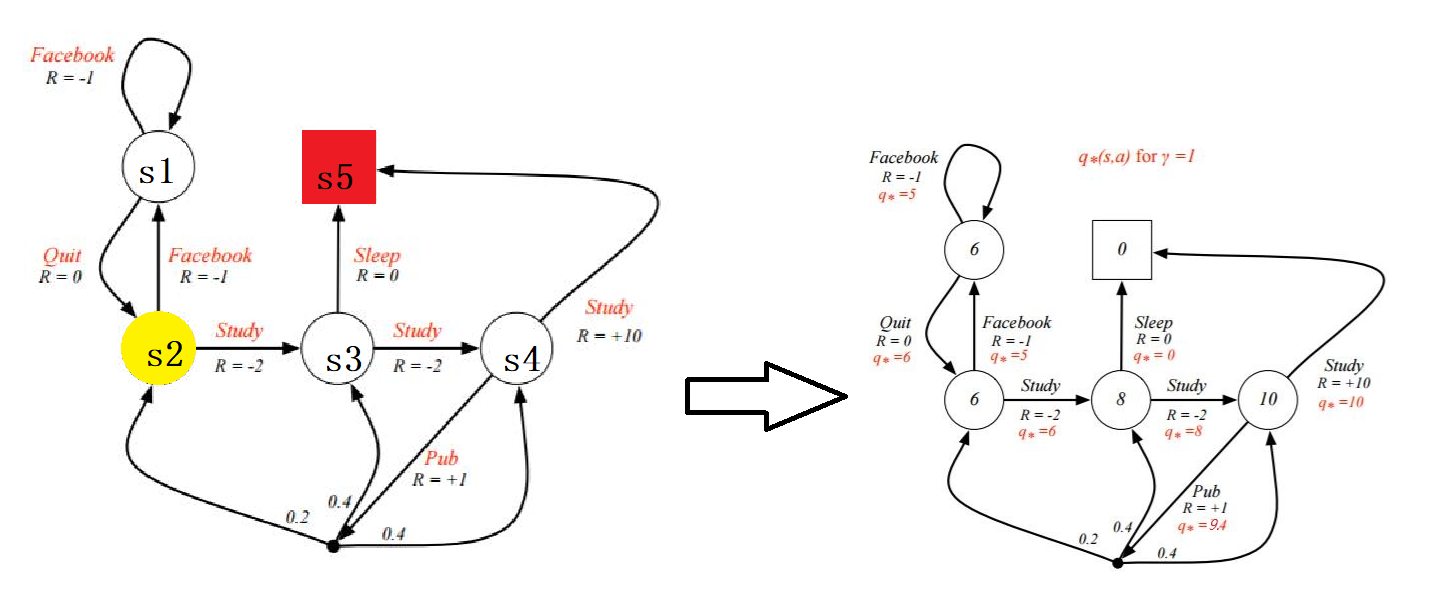
求解过程如下所示，过程稍微有点多，实在是不好使用Latex进行说明，就使用草稿纸进行推导了。

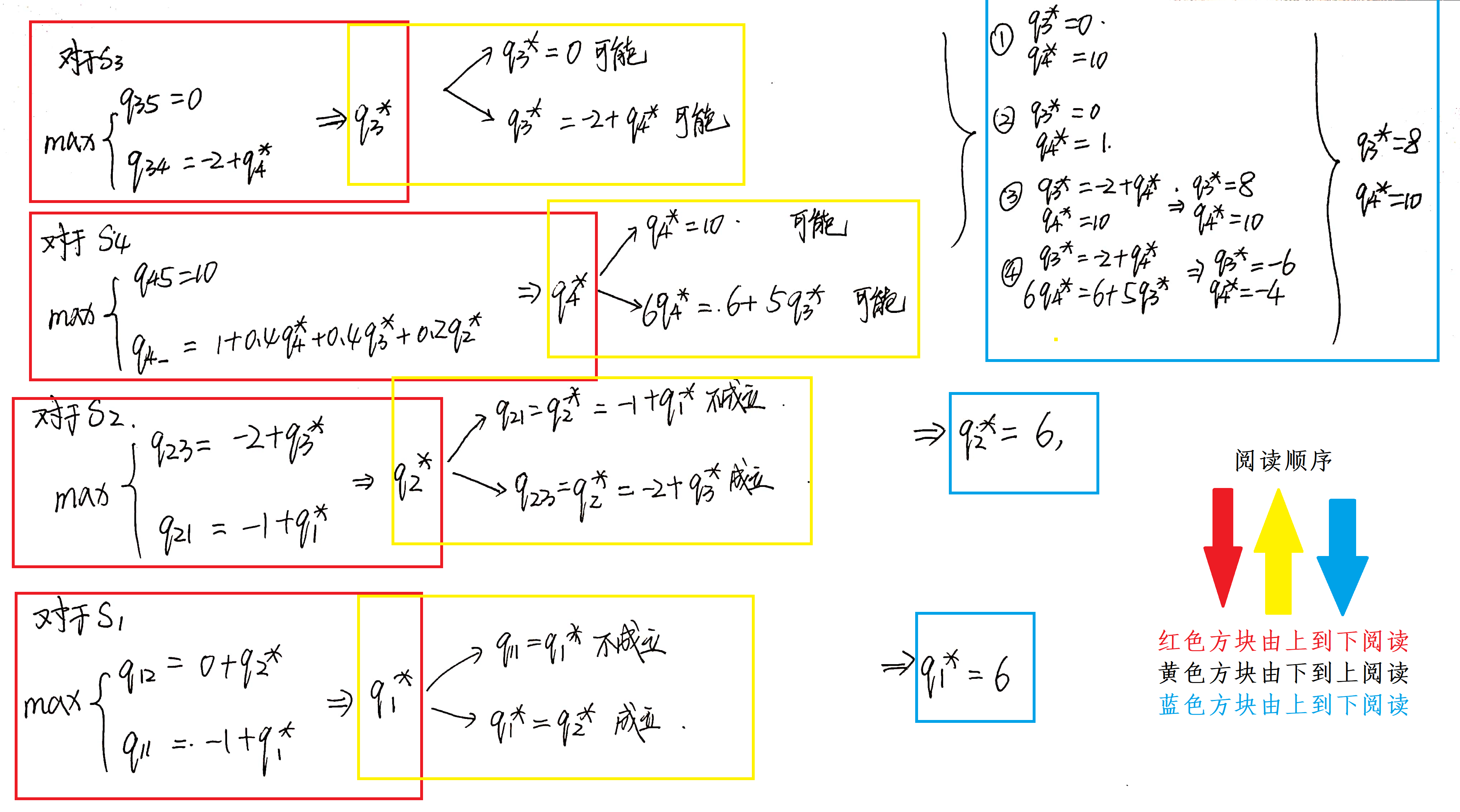
上面的部分是我们人为的推导方法 ，电脑肯定没有我们这么聪明，那么对于电脑来说，应该怎么进行推导呢？

求解方法

求解方法有很多种，下面将介绍一种最基本的动态规划算法。

动态规划

当问题具有下列两个性质时，通常可以考虑使用动态规划来求解：

1. 一个复杂问题的最优解由数个小问题的最优解构成，可以通过寻找子问题的最优解来得到复杂问题的最优解
2. 子问题在复杂问题内重复出现，使得子问题的解可以被存储起来重复利用，也就是说子问题之间存在递推关系，通过较小的子问题状态递推出较大的子问题的状态。

而强化学习刚好满足这个。为什么呢？因为bellman方程：

\[\begin{equation} v_\pi(s) =\mathbb{E}\left[R_{t+1}+\gamma v\left(S_{t+1}\right) | S_{t}=s\right] \\ v_{\pi}(s)=\sum_{a \in A} \pi(a | s)\left(R_{s}^{a}+\gamma \sum_{s^{\prime} \in S} P_{s s^{\prime}}^{a} v_{\pi}\left(s^{\prime}\right)\right) \end{equation} \]

我们可以将求解每一个状态的价值函数定义为子问题，因为递推的关系，我们可以使用上一此迭代得到的价值函数来更新此时的价值函数。（妙哉！！！）

强化学习有两个基本问题：

1. 预测(Prediction)：对给定策略（\(\pi\)），奖励（Reward），状态集（S），动作集（A），和状态转化该概率（P），衰减因子（\(\gamma\)），目标是求解基于该策略的价值函数 \(v_{\pi}\) 。
2. 控制(Control)：寻找一个最优策略的过程（实际上就是寻找最优的价值函数）。对给定奖励（Reward），状态集（S），动作集（A），和状态转化该概率（P），衰减因子（\(\gamma\)），求解最优价值函数 \(v_*\) 和最优策略 \(\pi_*\)。

策略评估求解预测问题

首先，我们来看如何使用动态规划来求解强化学习的预测问题，即求解给定策略的状态价值函数的问题。这个问题的求解过程我们通常叫做策略评估(Policy Evaluation)。

策略评估的基本思路是从任意一个状态价值函数开始，依据给定的策略，结合贝尔曼期望方程、状态转移概率和奖励同步迭代更新状态价值函数，直至其收敛，得到该策略下最终的状态价值函数。

—— 强化学习（三）用动态规划（DP）求解

首先假设我们已知第\(k\) 轮的状态价值函数，那么我们就可以得到第\(k+1\)轮的状态价值函数：

\[v_{k+1}(s) = \sum\limits_{a \in A} \pi(a|s)(R_s^a + \gamma \sum\limits_{s' \in S}P_{ss'}^av_{k}(s')) \]

同时又可以简化为：

\[\begin{equation}\mathbf{v}^{k+1}=\mathcal{R}^{\pi}+\gamma \mathcal{P}^{\pi} \mathbf{v}^{k}\end{equation} \]

这里引用Planning by Dynamic Programming中的一个例子：我们有一个4x4的宫格。只有左上和右下的格子是终止格子。该位置的价值固定为0，个体如果到达终止格子，则停止移动。个体在16宫格其他格的每次移动，得到的即时奖励\(R\)都是-1，若往边界走，则会返回到原来的位置（也就是下一个状态还是原来的地方）。个体只能上下左右移动，每次移动一个位置。衰减因子\(\gamma = 1\)，\(P=1\)。给定的策略是随机策略，每个方向的移动概率是\(0.25\)。

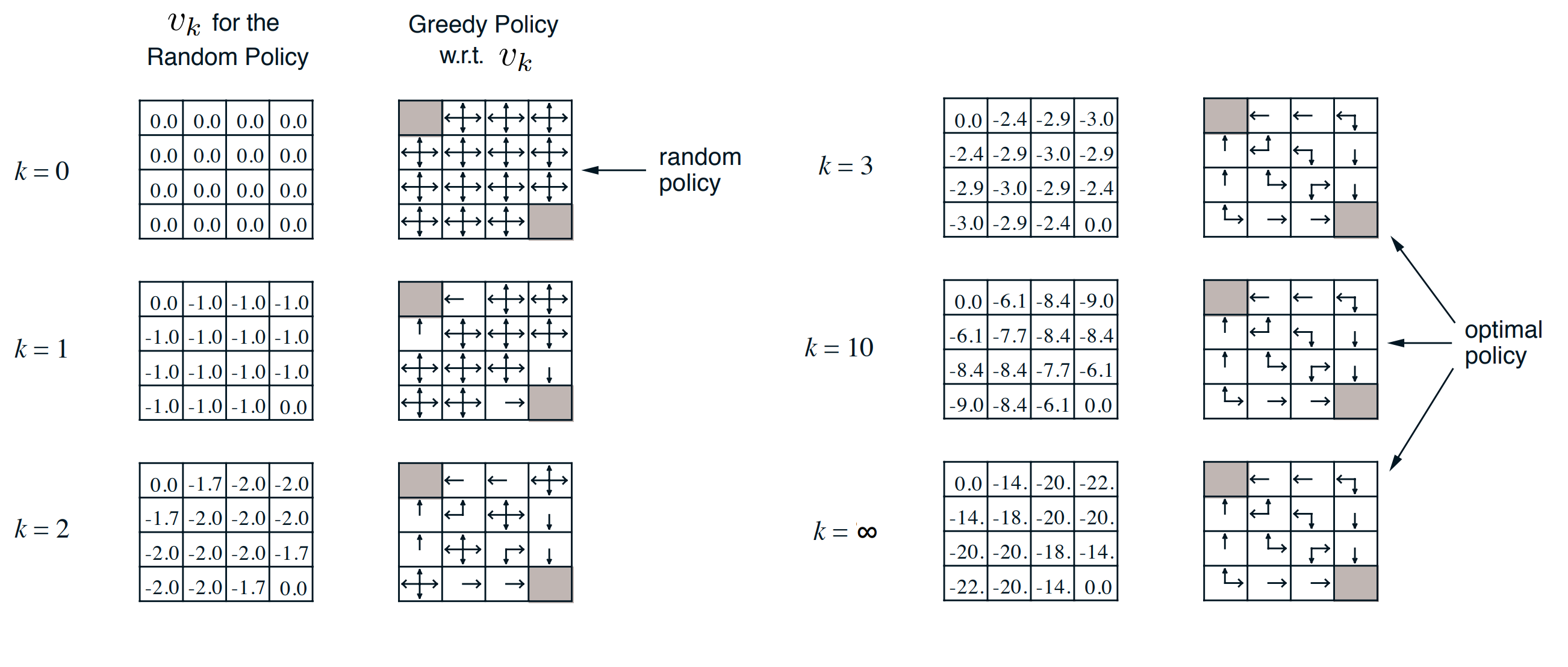
• K=1时：

  第一行第二个：

  \[\begin{equation}\begin{aligned} v^{(1,2)} &= 0.25[(R +v^{1,0}) + (R +v^{1,1}) + (R +v^{1,2}) + (R +v^{2,1})] \\&= 0.25\times[(-1 + 0) + (-1 + 0) + (-1 + 0) + (-1 + 0)] \\&= -1 \end{aligned}\end{equation} \]

  其他同理，结果如图所示。

• K=2时：

  第一行第二个：

  \[\begin{equation}\begin{aligned} v^{(1,2)} &= 0.25[(R +v^{1,0}) + (R +v^{1,1}) + (R +v^{1,2}) + (R +v^{2,1})] \\ &= 0.25\times[(-1 + 0) + (-1 + -1) + (-1 + -1) + (-1 + -1)] \\ &= \frac{7}{4} \\ &\approx-1.7 \end{aligned}\end{equation} \]

  然后我们一直这样迭代下去，直到每个格子的价值的变化小于某一个阈值时，我们会停止迭代。

  因此最终的得到结果如下：

  

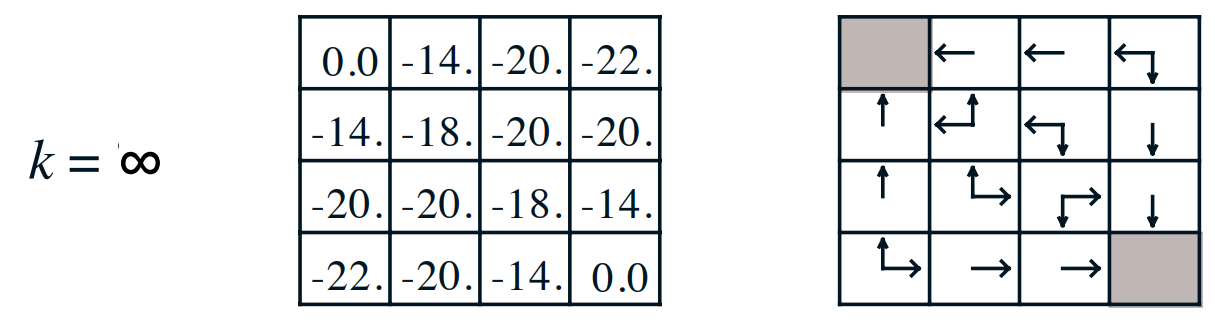
求解的过程并不复杂，当然，如果我们的数据很多的话，那么需要的迭代的次数也会增多。

策略迭代求解控制问题

针对于第二个控制问题，我们可以基于一种初始化策略，然后得到状态价值，然后在基于状态价值来及时的调整我们的策略，这个方法就叫做策略迭代（Policy Iteration）。过程示意图如下：

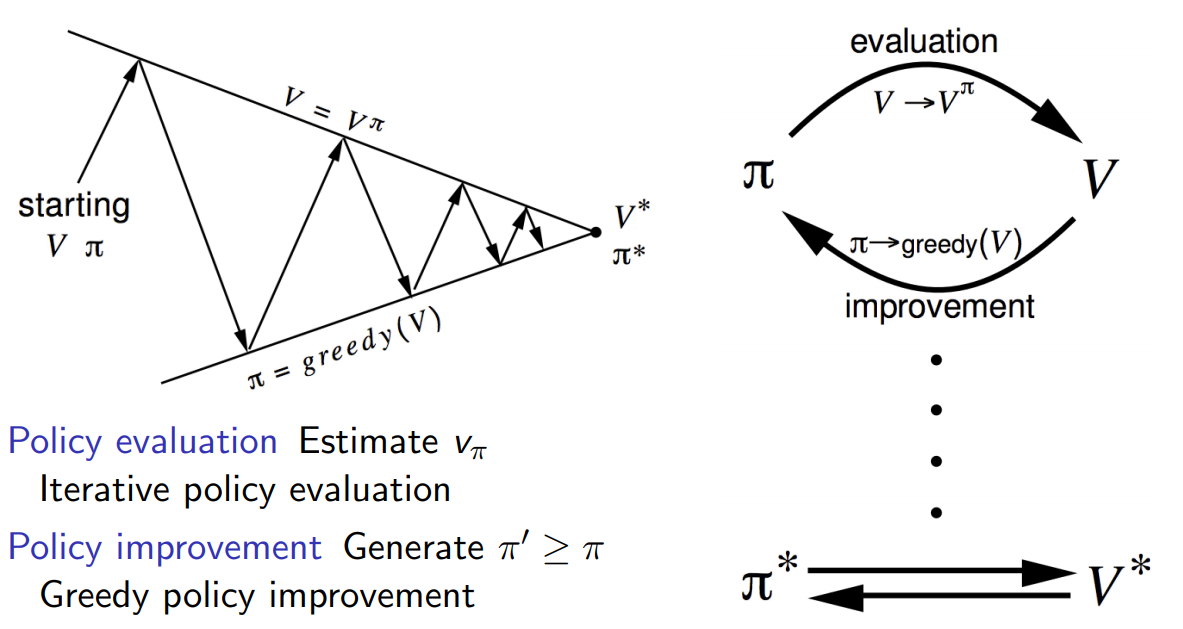
其中调整的方法是贪婪法。个体在某个状态下选择的行为是其能够到达后续所有可能的状态中状态价值最大的那个状态。算法的流程如下：

从算法中来看，实际上需要耗费的步骤还是挺多的。先进行价值迭代，然后又进行策略迭代，然后不符合的话又重复操作，一直迭代到价值和策略收敛才可以。

价值迭代求解控制问题

上述的策略迭代还有有一点问题，比如说上述的格子问题，实际上在\(k=3\)的时候就已经得到最优动作策略了：

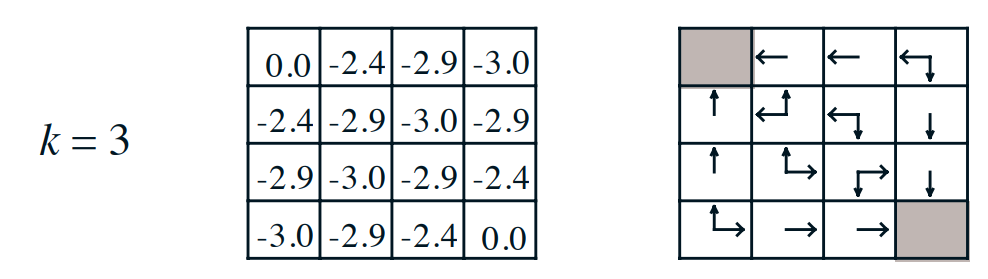
为了解决策略迭代出现的步骤多的问题，一个特殊的改进就是当策略评估仅进行一次更新的时候就停止。也就是说两者的区别如下：

1. 策略迭代：策略更新计算的是每一个状态\(s\)和各个行为\(a\)的期望值，然后进行更新旧值，直到\(v - V(s)\)小于某个阈值。然后在从其中选择最好的\(a\)。
2. 价值迭代：直迭代就是用某个行为 \(a\) 得到的最大的状态价值函数，来更新原来的状态价值函数，最后得到\(a\)。

算法的流程如下：

不过值得注意的是，以上动态规划得到的策略解\(\pi_*\)不一定是全局最优解，只是局部最优解。因此我们还需要使用探索率\(\epsilon\)，来跳出局部最优解。

总结

关于最佳策略的求解方法还有很多，比如说MC方法，时序差分方法等等，但是因为这个系列博客主要是为了快速入门到入土，就不那么详细的讲解了。如果想了解更多可以看看刘建平Pinard的强化学习。

在下一个篇博客中，将介绍Q-learning。

参考

• 强化学习（二）马尔科夫决策过程(MDP)
• 强化学习（三）用动态规划（DP）求解
• 强化学习 - 动态规划(Dynamic Programming)
• Planning by Dynamic Programming