深度神经网络(DNN,Deep Neural Networks)简介
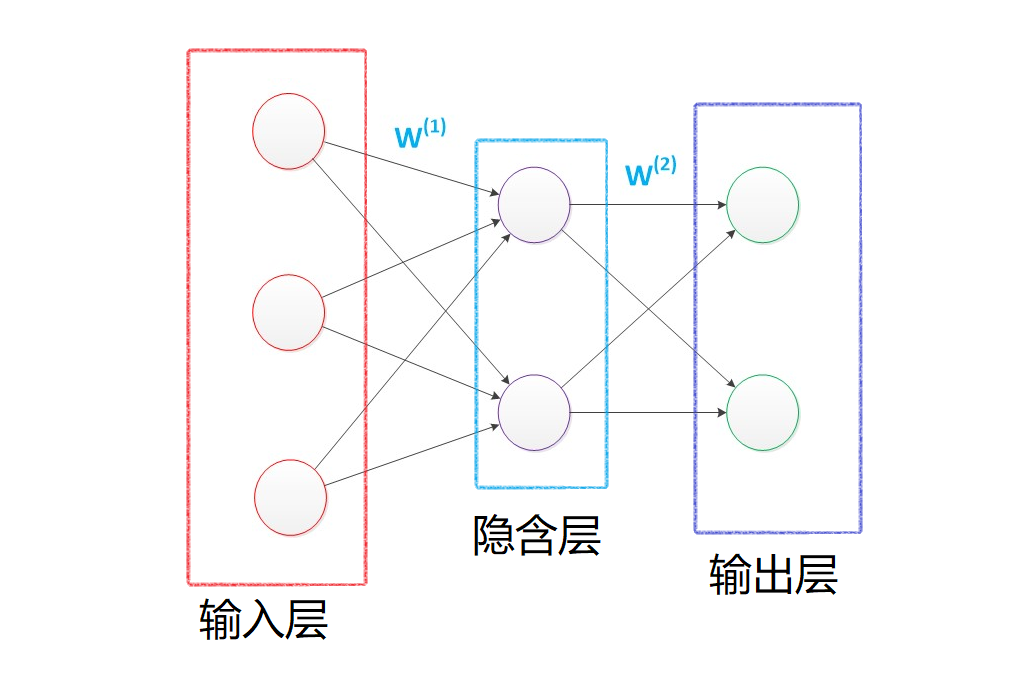
首先让我们先回想起在之前博客(数据挖掘入门系列教程(七点五)之神经网络介绍 )中介绍的神经网络:为了解决M-P模型中无法处理XOR等简单的非线性可分的问题时,我们提出了多层感知机,在输入层和输出层中间添加一层隐含层,这样该网络就能以任意精度逼近任意复杂度的连续函数。
然后在数据挖掘入门系列教程(八)之使用神经网络(基于pybrain)识别数字手写集MNIST 博客中,我们使用类似上图的神经网络结构对MINIST数据集进行了训练,最后在epochs = 100的条件下,F1 socre达到了约86 % 86 %
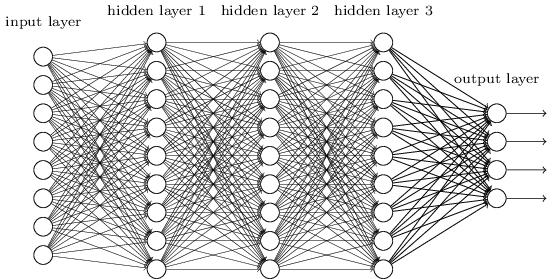
这个时候我们想一想,如果我们将中间的隐含层由一层变为多层,如下图所示:
那么该网络就变成了深度神经网络(DNN),也可以称之为多层感知机(Multi-Layer perceptron,MLP)。
下面将对这个网络进行介绍以及公式推导。
DNN的基本结构及前向传播
在上面的图中,我们可以很容易的观察到,在DNN中,层与层之间是全连接的,也就是如同感知机一样,第i i i + 1 i + 1
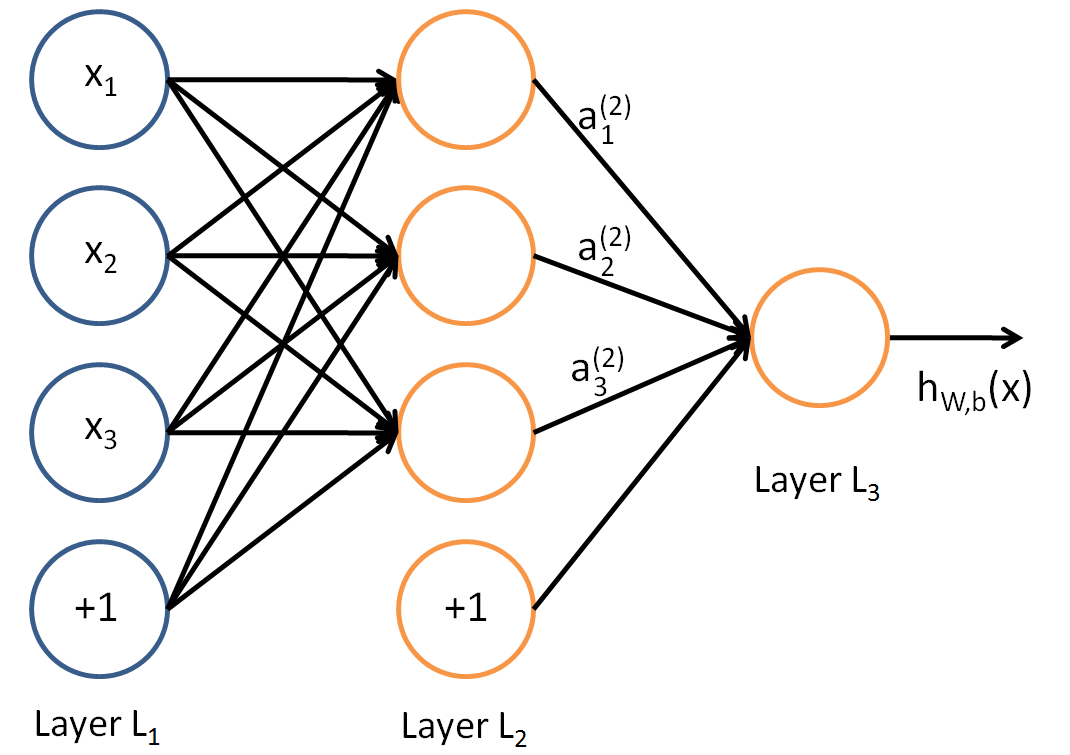
如同感知机,我们可以很简单的知道:
对于L a y e r L 2 L a y e r L 2
a 2 1 = σ ( z 2 1 ) = σ ( w 2 11 x 1 + w 2 12 x 2 + w 2 13 x 3 + b 2 1 ) a 2 2 = σ ( z 2 2 ) = σ ( w 2 21 x 1 + w 2 22 x 2 + w 2 23 x 3 + b 2 2 ) a 2 3 = σ ( z 2 3 ) = σ ( w 2 31 x 1 + w 2 32 x 2 + w 2 33 x 3 + b 2 3 ) (1) (1) a 1 2 = σ ( z 1 2 ) = σ ( w 11 2 x 1 + w 12 2 x 2 + w 13 2 x 3 + b 1 2 ) a 2 2 = σ ( z 2 2 ) = σ ( w 21 2 x 1 + w 22 2 x 2 + w 23 2 x 3 + b 2 2 ) a 3 2 = σ ( z 3 2 ) = σ ( w 31 2 x 1 + w 32 2 x 2 + w 33 2 x 3 + b 3 2 )
对于w w
对于w 3 24 w 24 3 w w w 3 24 w 24 3 w 3 42 w 42 3
在下图中,为了得到a a a = W x a = W x a = W T x a = W T x
对于L a y e r L 3 L a y e r L 3
a 3 1 = σ ( z 3 1 ) = σ ( w 3 11 a 2 1 + w 3 12 a 2 2 + w 3 13 a 2 3 + b 3 1 ) (2) (2) a 1 3 = σ ( z 1 3 ) = σ ( w 11 3 a 1 2 + w 12 3 a 2 2 + w 13 3 a 3 2 + b 1 3 )
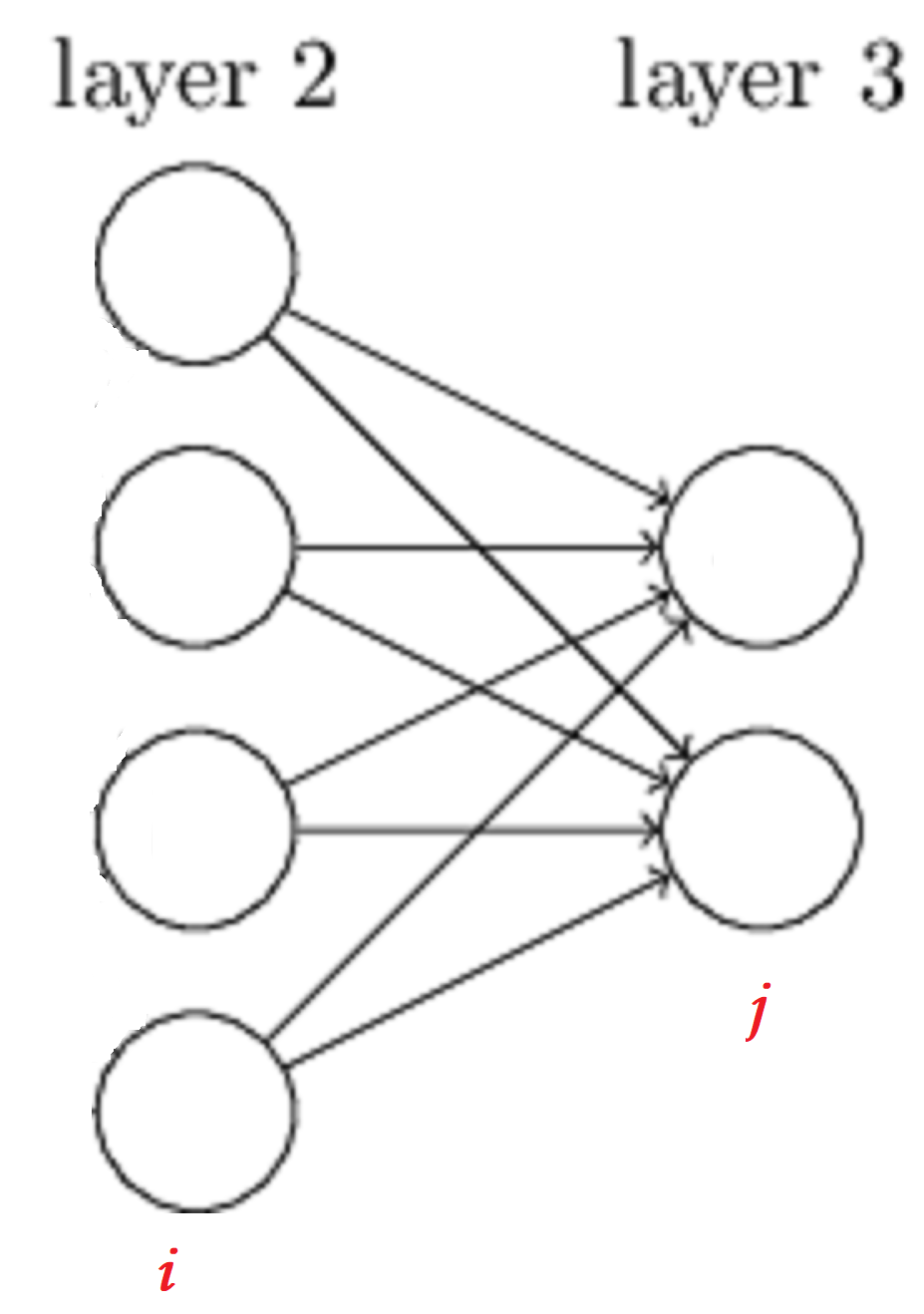
假设我们在l − 1 l − 1 m m l l j j a l j a j l
a l j = σ ( z l j ) = σ ( m ∑ k = 1 w l j k a l − 1 k + b l j ) (3) (3) a j l = σ ( z j l ) = σ ( ∑ k = 1 m w j k l a k l − 1 + b j l )
如果我们采用矩阵的方式进行表示,则第l l
a l = σ ( z l ) = σ ( W l a l − 1 + b l ) a l = σ ( z l ) = σ ( W l a l − 1 + b l )
因此,我们可以对DNN的前向传播算法进行推导,从输入到输出有:
输入: 总层数L L W W b b x x
输出:输出层的输出a L a L
1) 初始化a 1 = x a 1 = x
2) for l = 2 l = 2 L L
a l = σ ( z l ) = σ ( W l a l − 1 + b l ) (4) (4) a l = σ ( z l ) = σ ( W l a l − 1 + b l )
最后结果的输出即为a L a L
以上便是DNN的前向传播算法,实际上挺简单的,就是一层一层向下递归。
DNN反向传播(BP)算法
在数据挖掘入门系列教程(七点五)之神经网络介绍 中,我们提到过BP算法,并进行过详细的数学公式的推导。BP算法的目的就是为了寻找合适的W , b W , b L o s s L o s s
在DNN中,损失函数优化极值求解的过程最常见的一般是通过梯度下降法来一步步迭代完成的,当然也有其他的方法。而在这里,我们将使用梯度下降法对DNN中的反向传播算法进行一定的数学公式推导。图片和部分过程参考了Youtube:反向传播算法 ,但是对其中的某一些图片进行了修改。
在左边的图片中,是一个比较复杂的DNN网络,我们针对该DNN网络进行简化,将其看成每一层只有一个神经元的网络,如右图所示
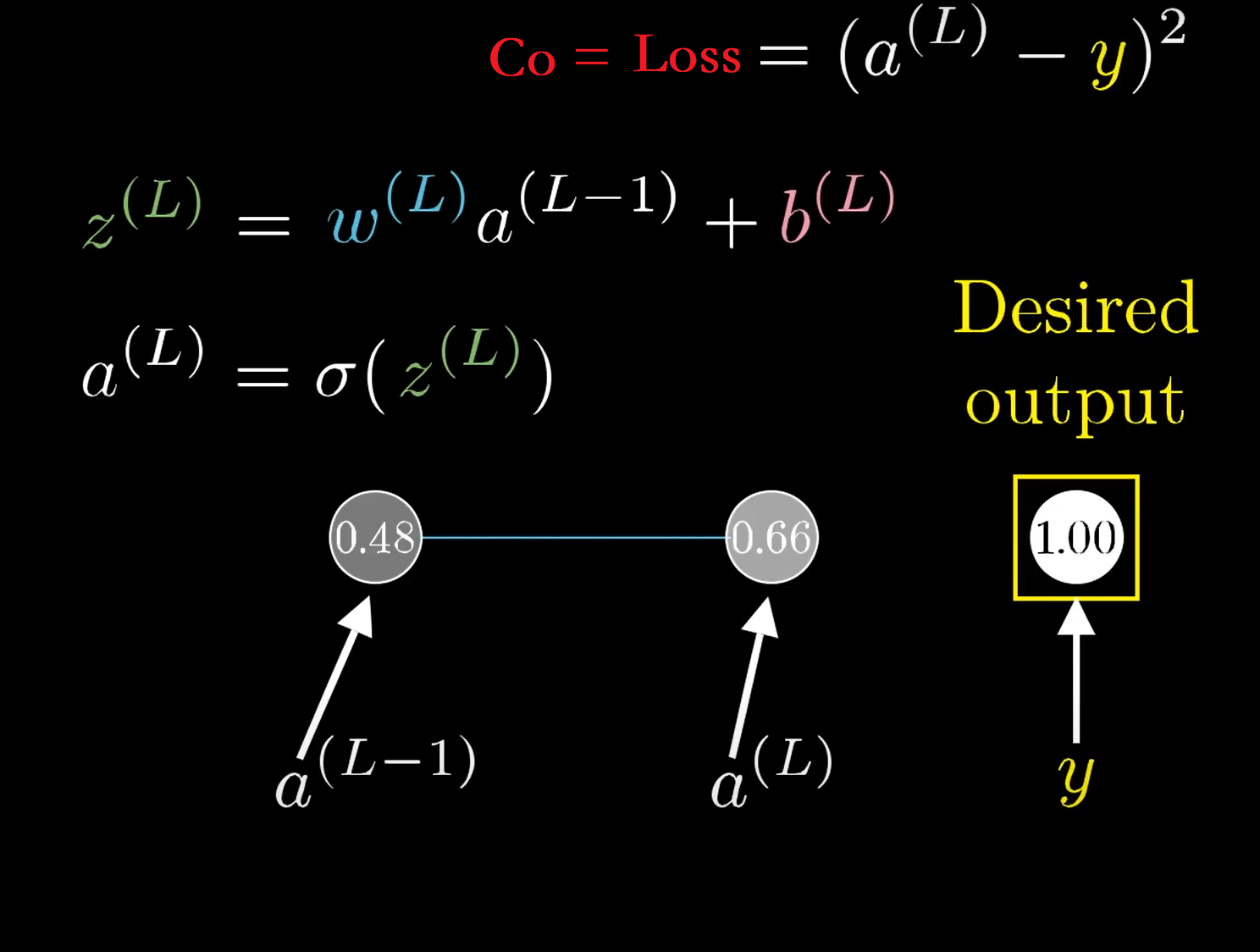
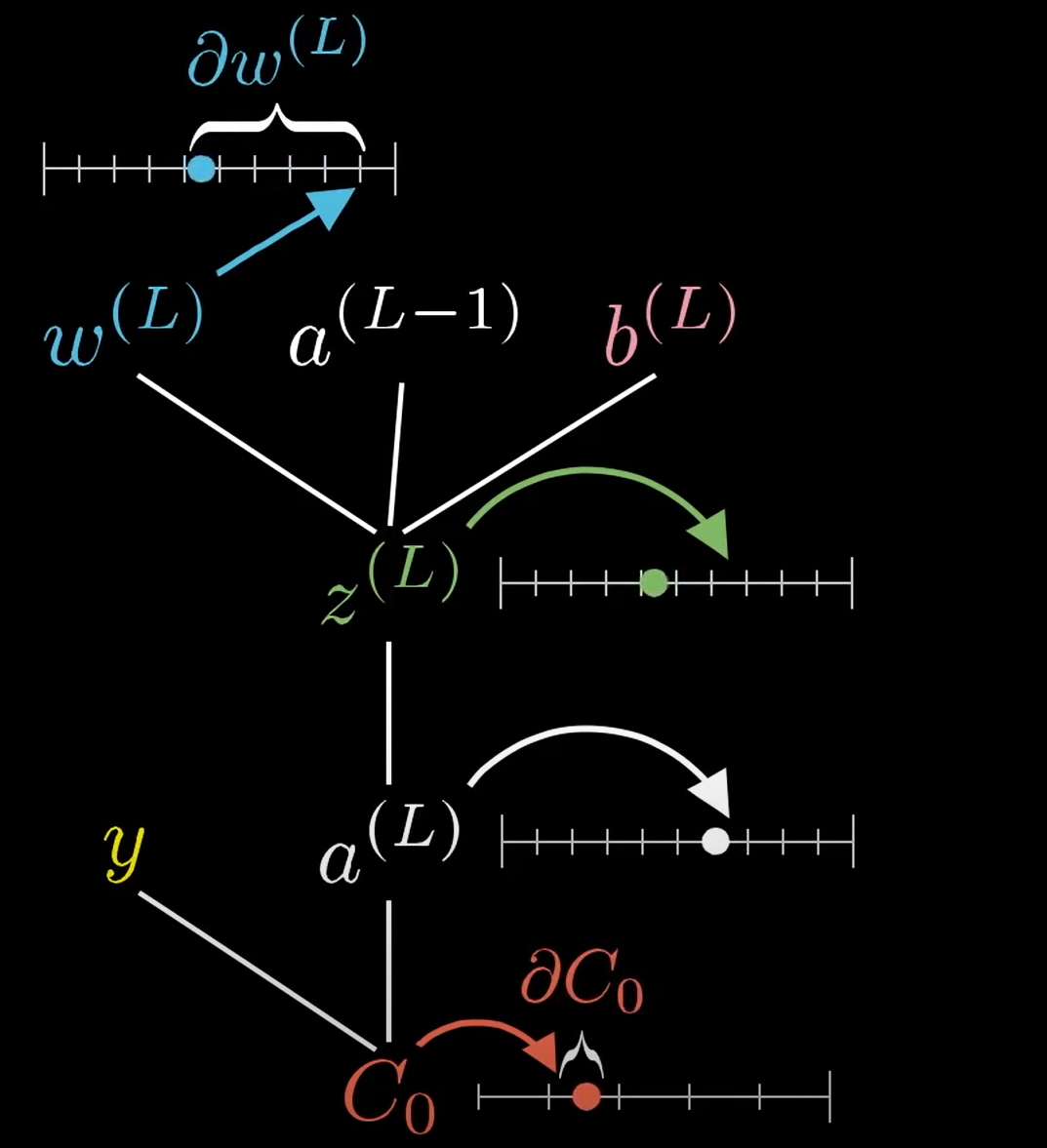
此时我们还可以将问题进行简化,如果我们只看简化模型的最后面两个神经元,则有:
y y C o C o C 0 = Loss = ( a ( L ) − y ) 2 C 0 = Loss = ( a ( L ) − y ) 2 σ σ
在下图所示,当w ( L ) w ( L ) ∂ w ( L ) ∂ w ( L ) C 0 C 0 ∂ w ( L ) ⟶ z ( L ) ⟶ a ( L ) ⟶ C 0 ∂ w ( L ) ⟶ z ( L ) ⟶ a ( L ) ⟶ C 0
此时我们对C 0 C 0 W L W L
∂ C 0 ∂ w ( L ) = ∂ z ( L ) ∂ w ( L ) ∂ a ( L ) ∂ z ( L ) ∂ C 0 ∂ a ( L ) (5) (5) ∂ C 0 ∂ w ( L ) = ∂ z ( L ) ∂ w ( L ) ∂ a ( L ) ∂ z ( L ) ∂ C 0 ∂ a ( L )
我们分别求各自偏导的结果:
∵ C 0 = ( a ( L ) − y ) 2 ∴ ∂ C 0 ∂ a ( L ) = 2 ( a ( L ) − y ) ∵ a ( L ) = σ ( z ( L ) ) ∴ ∂ a ( L ) ∂ z ( L ) = σ ′ ( z ( L ) ) ∵ z ( L ) = w ( L ) a ( L − 1 ) + b ( L ) ∴ ∂ z ( L ) ∂ w ( L ) = a ( L − 1 ) (6) (6) ∵ C 0 = ( a ( L ) − y ) 2 ∴ ∂ C 0 ∂ a ( L ) = 2 ( a ( L ) − y ) ∵ a ( L ) = σ ( z ( L ) ) ∴ ∂ a ( L ) ∂ z ( L ) = σ ′ ( z ( L ) ) ∵ z ( L ) = w ( L ) a ( L − 1 ) + b ( L ) ∴ ∂ z ( L ) ∂ w ( L ) = a ( L − 1 )
综上,结果为:
∂ C 0 ∂ w ( L ) = ∂ z ( L ) ∂ w ( L ) ∂ a ( L ) ∂ z ( L ) ∂ C 0 ∂ a ( L ) = a ( L − 1 ) σ ′ ( z ( L ) ) 2 ( a ( L ) − y ) (7) (7) ∂ C 0 ∂ w ( L ) = ∂ z ( L ) ∂ w ( L ) ∂ a ( L ) ∂ z ( L ) ∂ C 0 ∂ a ( L ) = a ( L − 1 ) σ ′ ( z ( L ) ) 2 ( a ( L ) − y )
同理我们可得:
∂ C 0 ∂ b ( L ) = ∂ z ( L ) ∂ b ( L ) ∂ a ( L ) ∂ z ( L ) ∂ C 0 ∂ a ( L ) = 1 σ ′ ( z ( L ) ) 2 ( a ( L ) − y ) (8) (8) ∂ C 0 ∂ b ( L ) = ∂ z ( L ) ∂ b ( L ) ∂ a ( L ) ∂ z ( L ) ∂ C 0 ∂ a ( L ) = 1 σ ′ ( z ( L ) ) 2 ( a ( L ) − y )
∂ C 0 ∂ a ( L − 1 ) = ∂ z ( L ) ∂ a ( L − 1 ) ∂ a ( L ) ∂ z ( L ) ∂ C 0 ∂ a ( L ) = w ( L ) σ ′ ( z ( L ) ) 2 ( a ( L ) − y ) (9) (9) ∂ C 0 ∂ a ( L − 1 ) = ∂ z ( L ) ∂ a ( L − 1 ) ∂ a ( L ) ∂ z ( L ) ∂ C 0 ∂ a ( L ) = w ( L ) σ ′ ( z ( L ) ) 2 ( a ( L ) − y )
这时候,我们可以稍微将问题复杂化一点,考虑多个神经元如下图所示,那么此时所有的变量W , x , b , z , a , y W , x , b , z , a , y
求导结果如下(这里我们使得Loss为J ( W , b , x , y ) = 1 2 ∥ ∥ a L − y ∥ ∥ 2 2 J ( W , b , x , y ) = 1 2 ‖ a L − y ‖ 2 2 W , b , x , y W , b , x , y
∂ J ( W , b , x , y ) ∂ W L = ∂ J ( W , b , x , y ) ∂ z L ∂ z L ∂ W L = ∂ J ( W , b , x , y ) ∂ a L ∂ a L ∂ z L ∂ z L ∂ W L = ( a L − y ) ⊙ σ ′ ( z L ) ( a L − 1 ) T ∂ J ( W , b , x , y ) ∂ b L = ∂ J ( W , b , x , y ) ∂ z L ∂ z L ∂ b L = ∂ J ( W , b , x , y ) ∂ a L ∂ a L ∂ z L ∂ z L ∂ b L = ( a L − y ) ⊙ σ ′ ( z L ) (10) (10) ∂ J ( W , b , x , y ) ∂ W L = ∂ J ( W , b , x , y ) ∂ z L ∂ z L ∂ W L = ∂ J ( W , b , x , y ) ∂ a L ∂ a L ∂ z L ∂ z L ∂ W L = ( a L − y ) ⊙ σ ′ ( z L ) ( a L − 1 ) T ∂ J ( W , b , x , y ) ∂ b L = ∂ J ( W , b , x , y ) ∂ z L ∂ z L ∂ b L = ∂ J ( W , b , x , y ) ∂ a L ∂ a L ∂ z L ∂ z L ∂ b L = ( a L − y ) ⊙ σ ′ ( z L )
注意上式中有一个符号⊙ ⊙ A ( a 1 , a 2 , … a n ) T 和 B ( b 1 , b 2 , … b n ) T , A ( a 1 , a 2 , … a n ) T 和 B ( b 1 , b 2 , … b n ) T , A ⊙ B = A ⊙ B = ( a 1 b 1 , a 2 b 2 , … a n b n ) T ( a 1 b 1 , a 2 b 2 , … a n b n ) T
假设第L − 1 L − 1 i i L L j j ∂ W ∂ W j × i j × i W W j × i j × i A ⊙ B A ⊙ B j × 1 j × 1 ( a L − 1 ) T ( a L − 1 ) T 的 矩 阵 ) ∗ 相 乘 , 最 后 结 果 则 为 一 个 的 矩 阵 ) ∗ 相 乘 , 最 后 结 果 则 为 一 个
在求导的结果∂ J ( W , b , x , y ) ∂ W L 和 ∂ J ( W , b , x , y ) ∂ b L ∂ J ( W , b , x , y ) ∂ W L 和 ∂ J ( W , b , x , y ) ∂ b L ∂ J ( W , b , x , y ) ∂ z L = ( a L − y ) ⊙ σ ′ ( z L ) ∂ J ( W , b , x , y ) ∂ z L = ( a L − y ) ⊙ σ ′ ( z L )
δ L = ∂ J ( W , b , x , y ) ∂ z L = ( a L − y ) ⊙ σ ′ ( z L ) (11) (11) δ L = ∂ J ( W , b , x , y ) ∂ z L = ( a L − y ) ⊙ σ ′ ( z L )
根据前向传播算法,对于与第l l W l 和 b l W l 和 b l
∂ J ( W , b , x , y ) ∂ W l = ∂ J ( W , b , x , y ) ∂ z l ∂ z l ∂ W l = δ l ( a l − 1 ) T ∂ J ( W , b , x , y ) ∂ b l = ∂ J ( W , b , x , y ) ∂ z l ∂ z l ∂ b l = δ l (12) (12) ∂ J ( W , b , x , y ) ∂ W l = ∂ J ( W , b , x , y ) ∂ z l ∂ z l ∂ W l = δ l ( a l − 1 ) T ∂ J ( W , b , x , y ) ∂ b l = ∂ J ( W , b , x , y ) ∂ z l ∂ z l ∂ b l = δ l
因此问题就变成了如何求得任意一层l l δ l δ l L L δ L δ L δ L = ( a L − y ) ⊙ σ ′ ( z L ) δ L = ( a L − y ) ⊙ σ ′ ( z L ) L − 1 L − 1
设第l + 1 l + 1 δ l + 1 δ l + 1 δ l δ l
δ l = ∂ J ( W , b , x , y ) ∂ z l = ( ∂ z l + 1 ∂ z l ) T ∂ J ( W , b , x , y ) ∂ z l + 1 = ( ∂ z l + 1 ∂ z l ) T δ l + 1 δ l = ∂ J ( W , b , x , y ) ∂ z l = ( ∂ z l + 1 ∂ z l ) T ∂ J ( W , b , x , y ) ∂ z l + 1 = ( ∂ z l + 1 ∂ z l ) T δ l + 1
也就是说,求解关键点又到了( ∂ z l + 1 ∂ z l ) T ( ∂ z l + 1 ∂ z l ) T
z l + 1 = W l + 1 a l + b l + 1 = W l + 1 σ ( z l ) + b l + 1 z l + 1 = W l + 1 a l + b l + 1 = W l + 1 σ ( z l ) + b l + 1
因此,有:
∂ z l + 1 ∂ z l = W l + 1 d i a g ( σ ′ ( z l ) ) ∂ z l + 1 ∂ z l = W l + 1 d i a g ( σ ′ ( z l ) )
综上可得:
δ l = ( ∂ z l + 1 ∂ z l ) T ∂ J ( W , b , x , y ) ∂ z l + 1 = d i a g ( σ ′ ( z l ) ) ( W l + 1 ) T δ l + 1 = ( W l + 1 ) T δ l + 1 ⊙ σ ′ ( z l ) δ l = ( ∂ z l + 1 ∂ z l ) T ∂ J ( W , b , x , y ) ∂ z l + 1 = d i a g ( σ ′ ( z l ) ) ( W l + 1 ) T δ l + 1 = ( W l + 1 ) T δ l + 1 ⊙ σ ′ ( z l )
因此当我们可以得到任意一层的δ l δ l W l 和 b l W l 和 b l
算法流程
下面算法流程是copy深度神经网络(DNN)反向传播算法(BP) 的,因为他写的比我好多了,我就直接用他的了。
现在我们总结下DNN反向传播算法的过程。由于梯度下降法有批量(Batch),小批量(mini-Batch),随机三个变种, 为了简化描述, 这里我们以最基本的批量梯度下降法为例来描述反向传播算法。实际上在业界使用最多的是mini-Batch的 梯度下降法。不过区别又仅在于迭代时训练样本的选择而已。
输入: 总层数L L α α M A X M A X ϵ ϵ m m { ( x 1 , y 1 ) , ( x 2 , y 2 ) , … , ( x m , y m ) } { ( x 1 , y 1 ) , ( x 2 , y 2 ) , … , ( x m , y m ) }
输出: 各隐藏层与输出层的线性关系系数矩阵 W W b b
初始化各隐藏层与输出层的线性关系系数矩阵W W b b
for iter to 1 to MAX:
2.1 for i = 1 i = 1 m m
a. 将DNN输入 a 1 a 1 x i x i l = 2 l = 2 L , L , a i , l = σ ( z i , l ) = σ ( W l a i , l − 1 + b l ) a i , l = σ ( z i , l ) = σ ( W l a i , l − 1 + b l ) δ i , L δ i , L l = l = δ i , l = ( W l + 1 ) T δ i , l + 1 ⊙ σ ′ ( z i , l ) δ i , l = ( W l + 1 ) T δ i , l + 1 ⊙ σ ′ ( z i , l ) l = 2 l = 2 L , L , l l W l , b l : W l , b l :
W l = W l − α ∑ m i = 1 δ i , l ( a i , l − 1 ) T b l = b l − α ∑ m i = 1 δ i , l W l = W l − α ∑ i = 1 m δ i , l ( a i , l − 1 ) T b l = b l − α ∑ i = 1 m δ i , l
2-3. 如果所有W , b W , b ϵ , ϵ ,
输出各隐藏层与输出层的线性关系系数矩阵W W b b
总结
这一篇博客主要是介绍了以下内容:
DNN介绍
DNN的基本结构
DNN的前向传播
DNN的BP算法
本来是想在这一章博客中将CNN也介绍一下,但是想了想,可能还是分开介绍比较好。因此我将会在下一篇博客中主要会对CNN进行介绍以及部分推导。
参考








【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· Linux系列:如何用heaptrack跟踪.NET程序的非托管内存泄露
· 开发者必知的日志记录最佳实践
· SQL Server 2025 AI相关能力初探
· Linux系列:如何用 C#调用 C方法造成内存泄露
· AI与.NET技术实操系列(二):开始使用ML.NET
· 无需6万激活码!GitHub神秘组织3小时极速复刻Manus,手把手教你使用OpenManus搭建本
· C#/.NET/.NET Core优秀项目和框架2025年2月简报
· Manus爆火,是硬核还是营销?
· 一文读懂知识蒸馏
· 终于写完轮子一部分:tcp代理 了,记录一下