数据挖掘入门系列教程（五）之Apriori算法Python实现
数据挖掘入门系列教程（五）之Apriori算法Python实现
在上一篇博客中，我们介绍了Apriori算法的算法流程，在这一片博客中，主要介绍使用Python实现Apriori算法。数据集来自grouplens中的电影数据，同样我的GitHub上面也有这个数据集。
推荐下载这个数据集，1MB大小够了，因为你会发现数据集大了你根本跑不动，Apriori的算法的复杂度实在是😔。
那么，这个我们使用数据集的作用是什么呢？简单点来说，就是某一个用户如喜欢看电影，那么他很可能也喜欢看
电影。我们就是需要分析这个关系。
万物始于加载数据集
加载数据集
因为下载的数据集是一个zip压缩包，首先，我们需要将数据解压出来：
import zipfile
zFile = zipfile.ZipFile("ml-latest-small.zip", "r")
#ZipFile.namelist(): 获取ZIP文档内所有文件的名称列表
for fileM in zFile.namelist():
zFile.extract(fileM)
解压出来的数据如下图：
主要介绍两个文件
- ratings.csv 每个用户对于电影的评分，包括movieId，userId，rating，time
- tags.csv 是电影的标签
我们目前只是使用rating.csv。然后我们将csv文件加载到内存中。
import pandas as pd
all_ratings = pd.read_csv("ml-latest-small/ratings.csv")
# 格式化时间，但是没什么必要
all_ratings["timestamp"] = pd.to_datetime(all_ratings['timestamp'],unit='s')
让我们看一看数据长什么样？
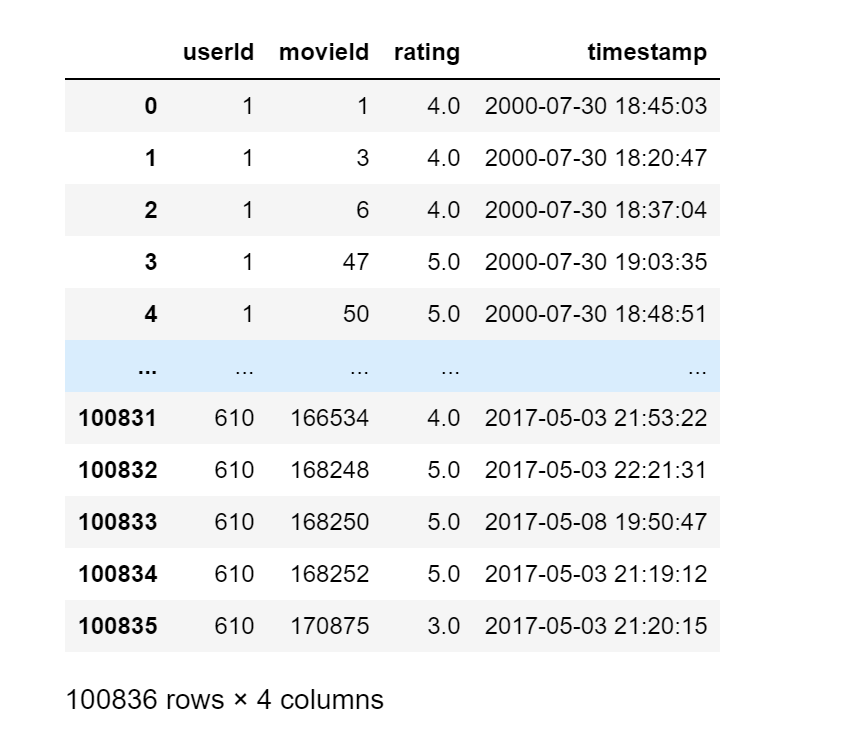
电影中的数据就是👆这副B样
- userId ：评分人的ID
- movieId：电影的ID
- rating：评分分数
- tiemstamp：评分时间
让我们来左手画个图，看一下rating数据的分布：
from eplot import eplot
df = all_ratings["rating"].value_counts()
df.eplot.bar(title='柱形图')
柱状图如下图：
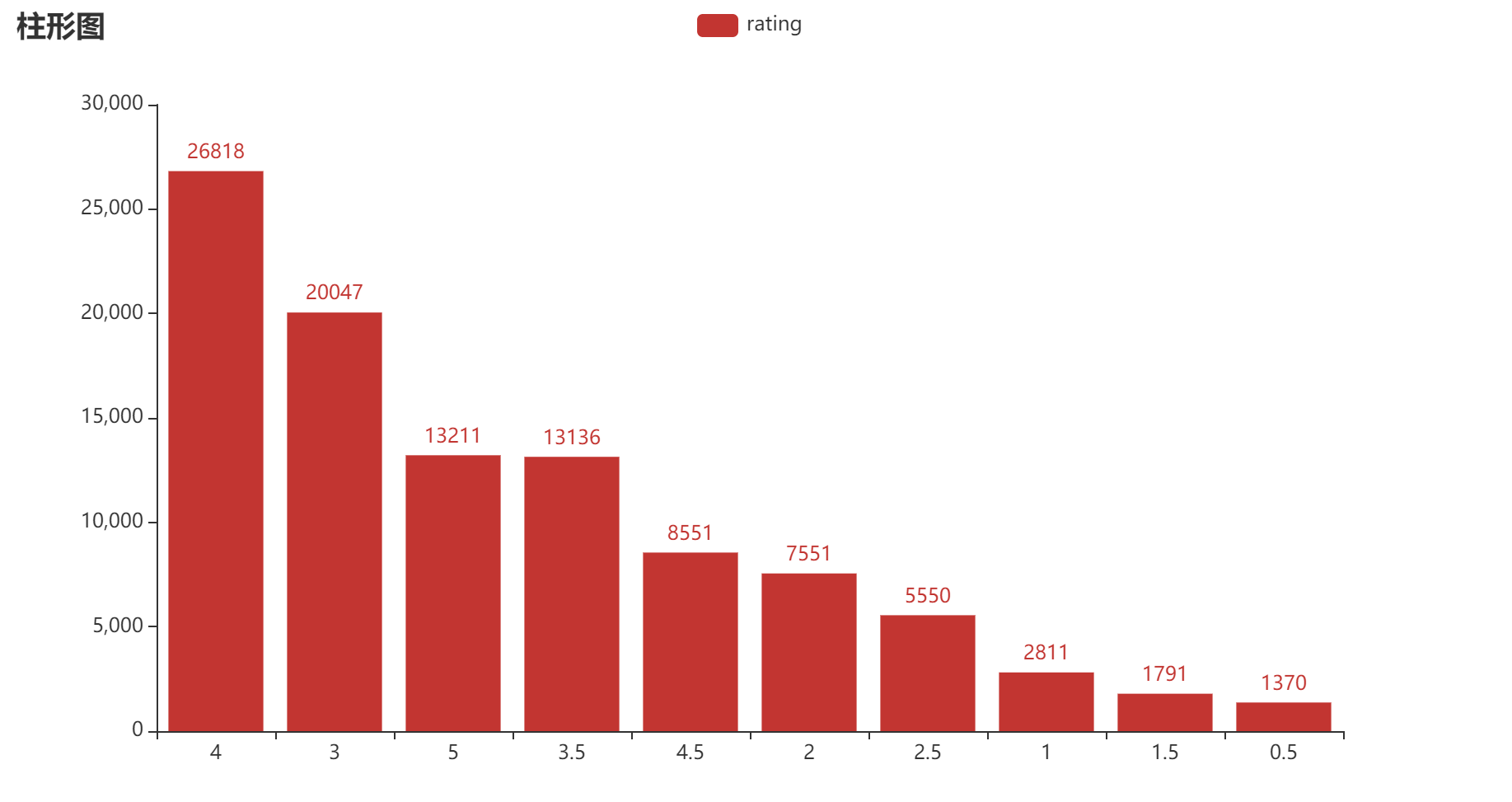
加载完数据集后。我们需要进行判断出用户是否喜欢某个电影，因此我们可以使用评分来判断。当用户对某一个电影的评分大于等于4分的时候，我们就可以认为该用户喜欢这部电影。
# 评分大于等于4分表示喜欢这个电影
all_ratings["like"] = all_ratings["rating"]>=4
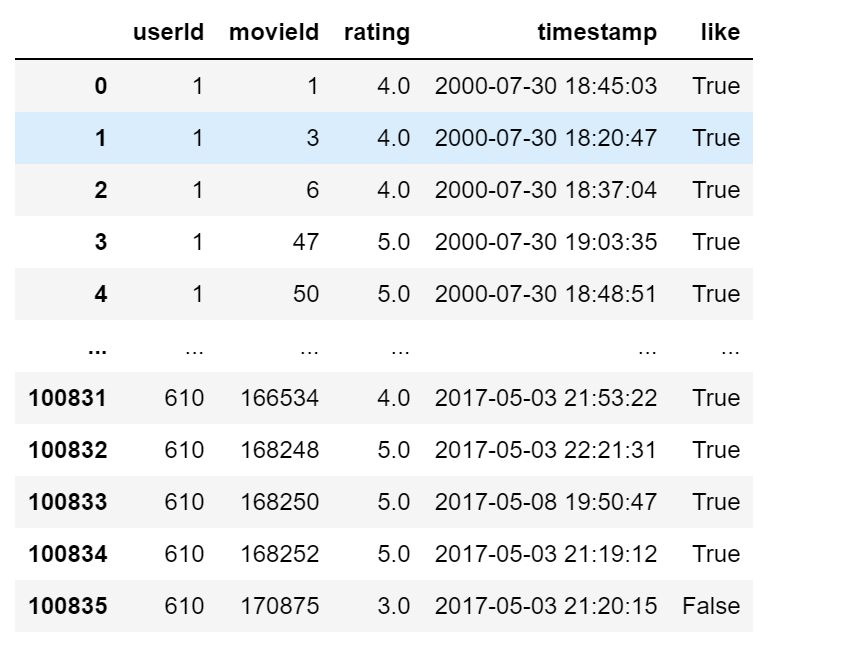
处理后的数据集如下，新的数据集添加了一个like列：
like为True代表喜欢，False为不喜欢。
获得训练集
在这里我们选择userId小于200的数据。
train_num = 200
# 训练数据
train_ratings = all_ratings[all_ratings['userId'].isin(range(train_num))]
数据格式如下：
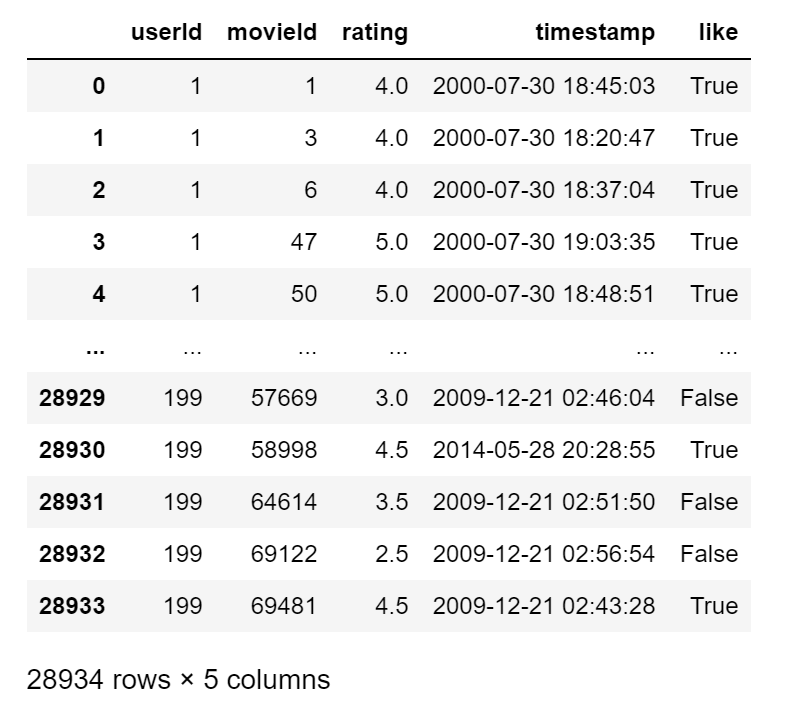
为什么只选择userId小于200的数据呢？而不大一点呢？emm，你电脑够好就行，自己看情况选择。在阿里云学生机上，推荐200吧，大了的话，服务直接GG了。
然后我们再从这个数据集中获得like=True的数据集。
like_ratings = train_ratings[train_ratings["like"] == True]
然后我们再从训练集中获得每一个用户喜欢哪一些电影，key对应的是用户的Id，value对应的是用户喜欢的电影。
# 每一个人喜欢哪一些电影
like_by_user = dict((k,frozenset(v.values)) for k,v in like_ratings.groupby("userId")["movieId"])
继续从训练集中获得每一部电影被人喜欢的数量。
# 电影被人喜欢的数量
num_like_of_movie = like_ratings[["movieId", "like"]].groupby("movieId").sum()
此时num_like_of_movie中like表示的是电影被人喜欢的数量。
到目前为止我们所有的数据集就都已经准备完成了，接下来就是生成频繁项。
频繁项的生成
算法的流程图的一个例子如下：
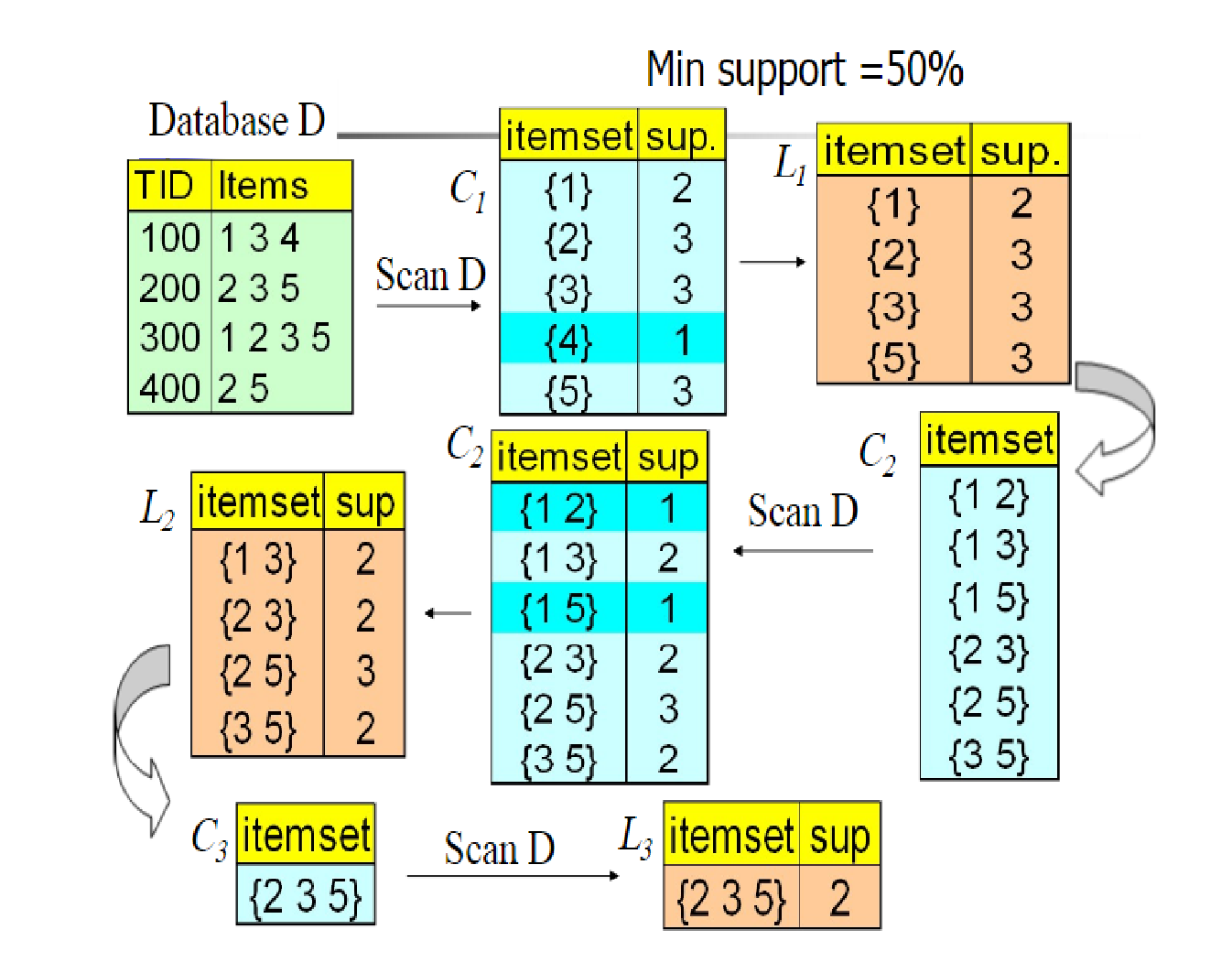
首先，我们生成初始频繁项集，也就是图中的。
ps：在本文中代表项集中每一项包含元素的个数（比如{A，B}中
，{A,B,C}中
）
下面代码与上图不同是我们使用的去除规则不同，规则是如果项集的数量少于min_support就去除。
# frequent_itemsets是一个字典，key为K项值，value为也为一个字典
frequent_itemsets = {}
min_support = 50
# first step 步骤一：生成初始的频繁数据集
frequent_itemsets[1] = dict((frozenset((movie_id,)),row["like"])
for movie_id,row in num_like_of_movie.iterrows()
if row["like"] > min_support)
在frequent_itemsets[1]中间，key为movie_id的集合，value为集合中电影被喜欢的数量。
frequent_itemsets[1]的数据如下（key = 1代表，value为数量）：
接下来我们就可以进行循环操作了，生成等情况。让我们定义一个方法。
# 步骤②③，
from collections import defaultdict
def find_new_frequent_items(movies_like_by_user,frequent_of_k,min_support):
"""
movies_like_by_user:每一个人喜欢电影的集合,也就是前面的like_by_user
frequent_of_k：超集，也就是前面例子图中的L1，L2等等
min_support:最小的支持度
"""
counts = defaultdict(int)
# 获得用户喜欢的movies的集合
for user,movie_ids in movies_like_by_user.items():
# 遍历超集中间的数据项
for itemset in frequent_of_k:
# 如数据项在用户的movie集合中，则代表用户同时喜欢这几部电影
if itemset.issubset(movie_ids):
# 遍历出现在movie集合但是没有出现在数据项中间的数据
for other_movie in movie_ids - itemset:
# current_superset为数据项和other_movie的并集
current_superset = itemset | frozenset((other_movie,))
counts[current_superset] += 1
# 去除support小于min_support的，返回key为数据项，value为support的集合
return dict([(itemset,support) for itemset,support in counts.items()
if support >= min_support])
这里值得注意的frozenset这个数据结构，即使里面的结构不同，但是他们是相等的：
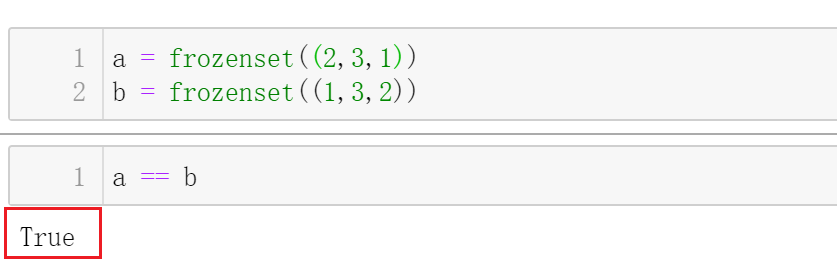
然后我们调用函数生成其他的项集。
for k in range(2,5):
current_set = find_new_frequent_items(like_by_user,frequent_itemsets[k-1],min_support)
if len(current_set) ==0:
print("{}项生成的备选项集长度为0，不再进行生成".format(k))
break
else:
print("准备进行{}项生成备选项集".format(k))
frequent_itemsets[k] = current_set
# 删除第一项（也就是k=1的项）
del frequent_itemsets[1]
此时，我们就已经得到的数据，如下（图中只截取了
的数据）。
生成规则
在上面我们获得了项集，接下来我们来进行构建规则。
以下图中{50,593,2571}为例子
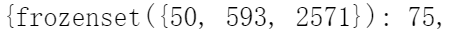
我们可以生成以下的规则：
其中前面一部分（绿色部分）表示用户喜欢看的电影，后面一部分表示如果用户喜欢看绿色部分的电影也会喜欢看红色部分的电影。可以生成项规则
生成规则的代码如下：
# 生成规则
rules = []
for k,item_counts in frequent_itemsets.items():
# k代表项数，item_counts代表里面的项
for item_set in item_counts.keys():
for item in item_set:
premise = item_set - set((item,))
rules.append((premise,item))
获得support
支持度挺好求的（实际上再上面已经得到support了），简单点来说就是在训练集中验证规则是否应验。比如说有{A,B},C规则，如果在训练集中某一条数据出现了A,B也出现了C则代表规则应验，如果没有出现C则代表规则没有应验。然后我们将规则是否应验保存下来（应验表示的是support，但是我们吧没有应验的也保存下来，目的是为了后面计算置信度）。
# 得到每一条规则在训练集中的应验的次数
# 应验
right_rule = defaultdict(int)
# 没有应验
out_rule = defaultdict(int)
for user,movies in like_by_user.items():
for rule in rules:
# premise,item代表购买了premise就会购买item
premise,item = rule
if premise.issubset(movies):
if item in movies:
right_rule[rule] +=1
else:
out_rule[rule] += 1
right_rule 保存的数据如下：
获得confidence
我们通过上面的right_rule和out_rule去求Confidence，在这篇博客中介绍了怎么去求置信度。
然后我们就可以计算出每一条规则的置信度，然后进行从大到小的排序：
# 计算每一条规则的置信度
rule_confidence = {rule:right_rule[rule]/float(right_rule[rule] + out_rule[rule]) for rule in rules}
from operator import itemgetter
# 进行从大到小排序
sort_confidence = sorted(rule_confidence.items(),key=itemgetter(1),reverse = True)
结果如下：
可以很明显的看到，有很多置信度为1.0的规则。前面的博客我们介绍了confidence存在一定的不合理性，所以我们需要去求一下Lift
获得Lift
Lift的具体解释在前一篇博客。公式如下：
因此我们直接去用去获得Lift即可。
首先我们需要获得训练集中的。
# 计算X在训练集中出现的次数
item_num = defaultdict(int)
for user,movies in like_by_user.items():
for rule in rules:
# item 代表的就是X
premise,item = rule
if item in movies:
item_num[rule] += 1
# 计算P(X) item_num[rule]代表的就是P(X)
item_num = {k: v/len(like_by_user) for k, v in item_num.items()}
接着继续计算每一条规则的lift
# 计算每一条规则的Lift
rule_lift = {rule:(right_rule[rule]/(float(right_rule[rule] + out_rule[rule])))/item_num[rule] for rule in rules}
from operator import itemgetter
# 进行排序
sort_lift = sorted(rule_lift.items(),key=itemgetter(1),reverse = True)
结果如下所示：
进行验证
验证的数据集我们使用剩下的数据集（也就是），在这里面测试数据集比训练集大得多：
# 去除训练使用的数据集得到测试集
ratings_test = all_ratings.drop(train_ratings.index)
# 去除测试集中unlike数据
like_ratings_test = ratings_test[ratings_test["like"]]
user_like_test = dict((k,frozenset(v.values)) for k,v in like_ratings_test.groupby("userId")["movieId"])
然后将规则代入到测试集中，检验规则是否符合。
# 应验的次数
right_rule = 0
# 没有应验的次数
out_rule = 0
for movies in user_like_test.values():
if(sort_lift[0][0][0].issubset(movies)):
if(sort_lift[0][0][1] in movies):
right_rule +=1
else:
out_rule +=1
print("{}正确度为：{}".format(i,right_rule/(right_rule+out_rule)))
我们使用lift最大的一项进行验证，也就是下图中被圈出来的部分。sort_lift[0][0][0]表示的是下图中红色框框圈出来的，sort_lift[0][0][1]表示是由绿色框框圈出来的。
然后我们可以得到结果：
同样我们可以使用confidence去验证，这里就不多做介绍了。同样，我们可以限定取值，也可以多用几个规则去验证选取最好的一个规则。
总结
通过上面的一些步骤，我们就实现了Apriori算法，并进行了验证（实际上验证效果并不好）。实际上，上面的算法存在一定的问题，因为训练集占数据集的比例太小了。但是没办法，实在是数据集太大，电脑计算能力太差，I5十代U也大概只能跑的数据。
项目地址：GitHub
参考
- 《Python数据挖掘入门与实践》
- 数据挖掘入门系列教程（四点五）之Apriori算法
