《算法》之查找
《算法》之查找
源代码地址
首先我们会使用符号表这个词来描述一张抽象的表格。 我们将信息(值)储存在里面,然后通过特定的键来搜索并获取这些信息。那么首先我们来定义这个符号表的抽象类。
public abstract class AbstractST<Key extends Comparable<Key>,Value>{
/**
* 将键值存入表中
* @param key
* @param value
*/
public abstract void put(Key key,Value value);
/**
* 通过key获得value
* @param key
* @return 若不存在则返回空
*/
public abstract Value get(Key key);
/**
* 通过key删除结点
* @param key
* @return
*/
public abstract Value delete(Key key);
/**
* 表中的键值对数量
* @return
*/
public abstract int size();
/**
* 判断是否为空
* @return
*/
public boolean isEmpty(){
return size() == 0;
}
/**
* 判断建是否存在
* @param key
* @return
*/
public boolean contains(Key key){
return get(key) != null;
}
/**
* 返回小于key的数量
* @param key
* @return
*/
public abstract int rank(Key key);
/**
* 返回排名为index 的键
* @param index
* @return
*/
public abstract Key select(int index);
}既然是查找,是一种算法, 他的实现需要依靠一定的数据结构来实现高效的算法 。所以我们之前构建的抽象类是有一定作用的,它定义了一些简单的API,而我们的目的便是要去实现它。
Q:我们仅仅学的是操作算法,学会怎么去使用get()就行了,为什么还要去学其他的操作呢?
A:学习这些操作并不是说为了让我们学得更多。相信知道“树”的同学都知道,在树中实现查找是一种很简单的工作,但是如何插入却并不简单,而插入却是为了更好的进行查找。特别是在平衡树中,添加删除节点往往意味着树的结构的改变。所以对于我们而言,并不是说仅仅说能够使用get()函数即可,而是应该能够写get(),put(),delete()等等函数。因为因为这些函数的作用,才能够让我们能够轻轻松松的使用get函数。
查找之链表和数组
无序的链表
首先我们需要说的是无序的链表, i这个没什么好说的。因为在无序的i情况下,没有什么骚操作,只能利用for循环一个一个地进行查找。下面将实现插入,查找和删除的功能。其他的功能较为简单,就不展示了。
package search;
public class SequentialSearch<Key extends Comparable<Key>,Value> extends AbstractST<Key,Value> {
private Node first;
private int size;
@Override
public void put(Key key, Value value) {
// 进行更新
for (Node x = first ; x!=null; x = x.next) {
if (x.key.equals(key)){
x.value = value;
return;
}
}
// 新的创建
first = new Node(key,value,first);
size ++;
}
@Override
public Value get(Key key) {
// 命中
for (Node x = first ; x!=null; x = x.next) {
if (x.key.equals(key)){
return x.value;
}
}
// 没有命中。
return null;
}
@Override
public Value delete(Key key) {
Node pre = first;
for (Node x = first;x!=null;pre = x, x = x.next){
if (x.key.equals(key)){
Value value = x.value;
pre.next = x.next;
return value;
}
}
return null;
}
@Override
public int size() {
return size;
}
…………省略了其他的方法
// 结点
private class Node{
Key key;
Value value;
Node next;
public Node(Key key,Value value,Node next){
this.key = key;
this.value = value;
this.next = next;
}
}
}性能分析:
| 无序链表 | 插入 | 删除 | 查找 | 空间 |
|---|---|---|---|---|
| 复杂度 | O(1) | O(n) | O(n) | O(n) |
有序数组的二分查找
看到有序,相信大家已经想到什么好的算法进行查找了吧——二分查找。yes,构建有序的数组,在插入,删除的时候依旧保持有序,在get()函数中,使用二分查找,便是我们需要做的事情。(在链表中我们没必要使用二分查找,因为在链表中我们没办法准确定位中间结点的位置)。
在进行put()之前,首先我们需要使用rank()函数来获取key在数组中的“排名”。
/**
* 返回小于key的数量
* 非递归二分查找
* @param key
* @return
*/
@Override
public int rank(Key key) {
// lo……hi代表二分查找的范围
int lo = 0,hi = size -1;
while(lo<=hi){
int mid = lo + ((hi-lo)>>1);
int result = key.compareTo(keys[mid]);
// 假如key 大于 keys[mid]则返回大于0的值
if (result > 0){
lo = mid + 1;
}
// 假如key 小于 keys[mid]则返回小于0的值
else if(result < 0){
hi = mid -1;
}
// 如果两个相等
else {
return mid;
}
}
return lo;
}接下来我们将实现put,delete,get。
package search;
public class BinarySearchST<Key extends Comparable<Key>,Value> extends AbstractST <Key,Value> {
private int size;
private Key[] keys;
private Value[] values;
public BinarySearchST(int capacity) {
keys = (Key[]) new Comparable[capacity];
values = (Value[]) new Comparable[capacity];
this.size = 0;
}
@Override
public void put(Key key, Value value) {
// 假如值是空的,则代表删除这个键
if (value == null){
delete(key);
}
int position = rank(key);
// 如果键存在则更新。之所以先【position < size 】是为了防止出现数组越界。
if (position < size && keys[position].compareTo(key) == 0){
values[position] = value;
return;
}
// 如果容量已经满了,则进行扩容到原来的两倍
if (size == keys.length){
resize(2*size);
}
// 为position这个位置腾出空间
for (int i = size; i > position ; i--) {
keys[i] = keys[i -1];
values[i] = values[i -1];
}
keys[position] = key;
values[position] = value;
size ++;
}
// 扩容操作
public void resize(int capacity){
Key[] newKeys = (Key[]) new Comparable[capacity];
Value[] newValues = (Value[]) new Comparable[capacity];
for (int i =0;i<size;i++){
newKeys[i] = keys[i];
newValues[i] = values[i];
}
keys = newKeys;
values = newValues;
}
@Override
public Value get(Key key) {
if (size == 0){
return null;
}
// 获得所在位置
int i = rank(key);
if (i<size && keys[i].compareTo(key) == 0){
return values[i];
}
else{
return null;
}
}
@Override
public Value delete(Key key) {
if (key == null){
return null;
}
int position = rank(key);
// 假如key不存在
if (position < size && key.compareTo(keys[position]) != 0){
return null;
}
// 假如超出范围
else if (position == size){
return null;
}
// 没有超出范围
Value returnValue = values[position];
for (int i = position;i < size - 1;i++){
keys[i] = keys[i+1];
values[i] = values[i+1];
}
size --;
// 减小容量
if (size>0 && size == keys.length/4){
resize(keys.length/2);
}
return returnValue;
}
// 省略其他等等操作(包括rank())
……
}
由上面我们可以知道,在有序数组中,二分查找以一件很令人高兴的事情,但是在插入中却并不是那么让人乐观。在添加数据的时候, 我们不仅仅是插入数据而已,还需要进行查找。
性能分析:
| 有序数组 | 插入 | 删除 | 查找 | 空间 |
|---|---|---|---|---|
| 复杂度 | O(n) | O(n) | O(lgn) | O(n) |
跳跃链表(skip list)
skip list 是一个很让人新奇的东西,尽管可能会对它很陌生,但是你却可以在redis中间看到它的身影。下面是跳跃链表的示意图(图源wiki):

在这张示意图中我们可以很简单的知道当我们需要去寻找6的时候只需要简单的3步:head->1->4->6。不得不说这个是一个让人幸喜的发现(感谢W. Pugh)。这里面说下个人的观点:
在前面我们介绍了有序数组中查找使用了二分法能够明显的降低时间复杂度,但是却无法降低插入的时间复杂(即使我们知道插入的位置在哪),这个是由数组的特性决定的(假如插入的值在数组的中间,后面的数据就不得不进行移动位置)。
而在链表中,即使我们却不得不进行遍历,才能查找到结点。而链表的插入的时间却又是很快的(它并不需要 进行移动位置)。
跳跃链表刚好集成了两者的优点,让我们能够更好的查找元素和插入元素。
在上面的示意图中,我们知道跳跃链表是按层进行构建,最下面的层就是一个普通的有序链表,而上面一层则是下面链表的“快速通道”,而每一层都是一个有序的链表。
在这里我们可以去考虑下在跳跃链表中结点有什么特点:
- 每一个结点有两个指针,一个指向下一个结点,一个指向下一层结点。
- 如果一个
第i层包含A结点,那么比i小的层都包含A结点(这一点从上面的图中可以含简单的看到)。
这个是一个Node的模型(这个图真画),它包含key,value,left,right,up,down。这个是一个双向循环链表。left指向前一个结点,right指后一个结点,up指向上面一层的结点,down指向下面一层的结点。ps:不过如果Node不在第一层,则Node中Value没有什么存在的意义,也就是说value可以为空。

我们可以简单的定义一下跳跃链表需要实现的API。
- 查找
- 插入
- 删除
首先,让我们来定义一下SkipList的成员结构。在类中,有前面的Node,这个是数据的保存位置和方式。在head和tail中,这两个都是空的,不保存数据,只作为跳跃链表开始和结束的标志位。
public class SkipList<Key extends Comparable<Key>,Value>{
// 首先我们先定义好结点。
private class Node{
Key key;
Value value;
Node up;
Node down;
Node right;
Node left;
public Node(Key key, Value value){
this.key = key;
this.value = value;
}
}
// 当前跳表最大层数
private int maxLevel;
// 当前插入结点的个数
private int size;
// 首结点
private Node head;
// 尾结点
private Node tail;
public SkipList() {
maxLevel = 0;
// 创建首尾结点
head = new Node(null,null);
tail = new Node(null,null);
head.right = tail;
tail.left = head;
size = 0;
}
}下面以前面的图为例,来说下查找的方法。

/**
* 通过key获得node(node不一定是正确的)
* @param key
* @return 返回的node.key <= key
*/
public Node getNode(Key key) {
if (key == null){
return null;
}
Node node = head;
while(true){
/**
* 假如node.right不为尾结点且key.value大于或者等于右边结点的key
*/
while (node.right.key != tail.key && key.compareTo(node.right.key) >= 0){
node = node.right;
}
if (node.down != null){
node = node.down;
}else {
break;
}
}
// 返回的node.key <= key
return node;
}大家看到上面的方法,可能会很疑惑,为什么我们进行查找的时候,既然可能得到的node.key != key,为什么还要使用getNode方法呢?大家想一想前面的二分查找,在前面我们使用二分查找得到的lo所对应的位置难道就是key的位置吗?不是,我们之所以这样做就是为了在put()的时候能够重新使用这个方法。
这个才是真正的获取value的方法:
/**
* 通过key获得value
* @param key
* @return
*/
public Value get(Key key){
if (key == null){
return null;
}
Node node = getNode(key);
if (node.key.compareTo(key) == 0){
return node.value;
}else {
return null;
}
}
查找很简单,在跳跃链表中,难的是put和delete。
下面我将介绍一下put的方法。在前面我们说过,跳跃链表是由层构建的,当我们插入一个数据的时候,这个数据该有几层呢,谁来决定它的层数?天决定,对,就是天决定。我们使用随机数来决定层数。
- 如果存在则修改。
- 如果put的key值在跳跃链表中不存在,则进行新增节点,而高度由“天决定”。
- 当新添加的节点高度达到maxLevel(即跳跃链表中的最大level),则在head和tail添加一个新的层,这个层由head指向tail,同时maxLevel+1。
首先让我们将添加新的一层的代码完成。
/**
* 添加新的一层
*/
public void addEmptyLevel(){
Node newHead = new Node(null,null);
Node newTail= new Node(null,null);
newHead.right = tail;
tail.left = newHead;
newHead.down = head;
newTail.down = tail;
head.up = newHead;
tail.up = newTail;
head = newHead;
tail = newTail;
maxLevel ++;
}然后我们就可以开开心心的完成put的函数了。
public void put(Key key, Value value) {
// Key不能为null
if (key == null){
return;
}
// 插入的合适位置
Node putPosition = getNode(key);
// 如果相等则更新
if (key.equals(putPosition.key)){
putPosition.value = value;
return;
}
// 进行新增操作
Node newNode = new Node(key,value);
/**
* putPostion的key小于key,所以排序位置应该是
* putPosition 【newNode】 putPosition.next
* 所以进行下面的操作
*/
newNode.right = putPosition.right;
newNode.left = putPosition;
putPosition.right.left = newNode;
putPosition.right = newNode;
Random random = new Random();
int level = 0;
// 产生0和1,使得新的结点有1/2的几率去增加level
while (random.nextInt(2) == 0){
// 假如高度达到了maxLevel则添加一个层
if (level >= maxLevel){
addEmptyLevel();
}
while (putPosition.up == null){
putPosition = putPosition.left;
}
putPosition = putPosition.up;
// 可以将skipNode中的value设置为空,不过为空也没什么关系
Node skipNode = new Node(key, null);
/**
* 需要的顺序是:
* putPosition 【skipNode】 putPosition.right
*/
skipNode.left = putPosition;
skipNode.right = putPosition.right;
putPosition.right.left = skipNode;
putPosition.right = skipNode;
// 将newNode放到上一层
/**
* putpostion skipNode skipNode.right
* newNode
*/
skipNode.down = newNode;
newNode.up = skipNode;
newNode = skipNode;
level ++;
}
size ++;
}大家可以在代码中,发现随机的几率为0.5(这个可以去自己设置,同样也可以根据size的大小去设置),那么既然几率是0.5,那么有多少的结点有2层,有多少的结点有3层呢…….根据概率论的知识我们知道:
2层——>N*1/2,3层——>N*1/2*1/2,所以根据等比数列我们可以知道,除第1层以外所有的层数一共有N层
所以跳跃链表中一共有2N个结点。
性能分析:
| 跳跃数组 | 插入 | 删除 | 查找 | 空间 |
|---|---|---|---|---|
| 复杂度 | O(lgn) | O(lgn) | O(lgn) | O(n/p)【p代表随机的概率】 |
在前面我们讲的都是链表和数组的查找,无疑跳跃链表是最高效的,尽管它的操作相比数组和链表繁琐很多,但是O(logn)的时间复杂度和O(2N)的空间复杂度却能够让人很欣喜接受这一切。接下来我将介绍树的查找。
我家门前有几棵树
在前面, 我们使用线性的数据结构来储存数据,现在我们将用树来表达数据。这里我不会详细的介绍树,大家有可以去看看别人写的博客。
下面是维基百科对于树的介绍:
树的介绍
在计算机科学中,树(英语:tree)是一种抽象数据类型(ADT)或是实现这种抽象数据类型的数据结构,用来模拟具有树状结构性质的数据集合。它是由n(n>0)个有限节点组成一个具有层次关系的集合。把它叫做“树”是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。它具有以下的特点:
- 每个节点都只有有限个子节点或无子节点;
- 没有父节点的节点称为根节点;
- 每一个非根节点有且只有一个父节点;
- 除了根节点外,每个子节点可以分为多个不相交的子树;
- 树里面没有环路(cycle)
树的种类
- 无序树:树中任意节点的子节点之间没有顺序关系,这种树称为无序树,也称为自由树;
- 有序树:树中任意节点的子节点之间有顺序关系,这种树称为有序树;
二叉查找树(BST)
下面是一张二叉查找树的模型:

二叉查找树有一下特点:
- 若某结点的左子树不为空,则左子树上面所有的节点的值都小于该节点。【8大于左边所有的值】
- 若某结点的右子树不为空,则右子树上面所有的节点的值都大于该节点。【8小于右边所有的值】
- 没有键相等的节点(也就是说所有节点的key都不相等)
接下来定义一下二叉查找树的数据结构:
public class BST<Key extends Comparable<Key>,Value> extends AbstractST <Key,Value> {
// 根节点
private Node root;
private class Node{
private Key key;
private Value value;
private Node left,right;
// 以该结点为根的子树中结点总数,包括该节点
private int N;
public Node(Key key, Value value, int n) {
this.key = key;
this.value = value;
this.N = n;
}
}
/**
* 查看是否含有key
* @param key
* @return
*/
public boolean containsNode(Key key){
if (key == null){
return false;
}
Node node = root;
int temp;
while (node!= null) {
temp = node.key.compareTo(key);
// 假如key小于结点的key,则转向左子树
if (temp > 0) {
node = node.left;
} else if (temp < 0) { // 转向右子树
node = node.right;
} else {
return true;
}
}
return false;
}
/**
* 获得查找二叉树中所有结点的数量
* @return
*/
@Override
public int size() {
return size(root);
}
/**
* 获得以某结点为根所有子树结点的数量(包括该结点)
* @param node
* @return
*/
public int size(Node node){
if (node == null){
return 0;
}
return node.N;
}
……省略一些了继承过来的方法
}在前面我们知道了二叉查找树的特点,那么根据这些特点可以很简单的写查找算法。
- 查找
@Override
public Value get(Key key) {
// 默认返回值为空
Value resultValue = null;
// 假如key为空或则二叉树为空
if (key == null){
return resultValue;
}
Node node = root;
int temp;
// 可以使用递归或者非递归实现
while (node!= null && (temp=node.key.compareTo(key)) != 0){
// 假如key小于结点的key,则转向左子树
if (temp>0){
node = node.left;
}else if (temp < 0){ // 转向右子树
node = node.right;
}else {
resultValue = node.value;
break;
}
}
return resultValue;
}二叉查找树的查找还是比较简单的,无非就是当key比结点的key大的时候,则转向右子树,小于则转向左子树。
- 插入
下面让我们来说说插入函数吧,在插入的同时,我们还要不断的更新N(以该结点为根的子树中结点总数,包括该节点)。插入的操作已经在注释里面写的很详细了。
@Override
public void put(Key key, Value value) {
if(key == null){
return;
}
// 假如二叉树是空的
if (root == null){
root = new Node(key,value,1);
return;
}
int addN = 1;
// 假如树中含有key,则进行更新,所以树中的N就不需要发生变化。
if (containsNode(key)){
addN = 0;
}
int temp;
Node node = root;
while(true){
temp = node.key.compareTo(key);
// key相等则进行更新
if (temp == 0){
node.value = value;
return;
}
// 插入的key比node的key小,转向左子树
if (temp>0){
node.N += addN;
if (node.left == null){
node.left = new Node(key,value,1);
}
node = node.left;
}else {
node.N += addN;
if (node.right == null){
node.right = new Node(key,value,1);
}
node = node.right;
}
}
}-
删除
删除应该可以说是树中最难的一个操作了。在查找二叉树中,删除分为一下3种情况:
-
删除的结点是一个叶子结点,也就是说结点没有子节点。这种情况最容易处理。图源【在这位大佬的博客中,很生动形象的讲了删除的操作】。在这种情况下,我们可以直接将图中的
结点7.right = null即可。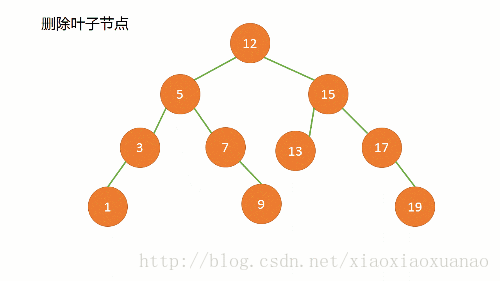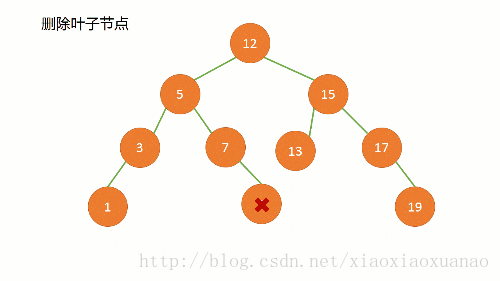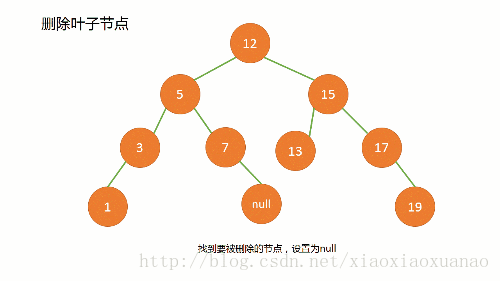
删除叶子结点 -
要删除的结点有一个子节点。这种情况也不复杂,如图所示的操作即可,同时被删除的结点的子节点上升了一个层次。

有一个子节点 -
要删除的结点有两个子节点,这种情况是最复杂的。因为父节点的left或者right无法同时指向被删除结点的两个子节点。解决这这个问题的方案有两种方案:合并删除和复制删除。
合并删除
首先先说一下合并删除,先给搭建看一看来自geeksforgeeks的一张图(稍微修改了一下)。
为什么叫合并删除呢?因为合并删除的思想就是将被删除节点的两个子节点合并成一棵树,然后代替被删除结点的位置,下面我将根据下图来讲一下具体的操作。
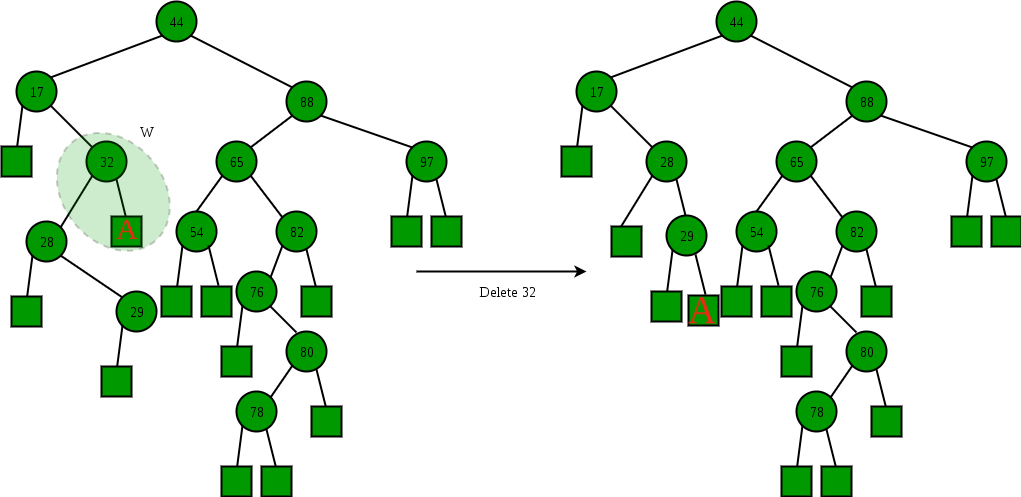
合并删除在图中我们需要删除的结点是
32:- 首先我们在删除结点的左子树找到最右边的结点X(也就是图中是结点29)。
- 然后将结点X的右子节点指向被删除结点的右子节点。(也就是将29结点的右子节点指向结点A)。
- 最后使得被删除结点的父节点指向被删除结点的左子结点。(也就是17结点指向28结点)。
我们可以想一想为什么要这么做?根据二叉查找树的性质我们可以很简单的知道,A子树是一定大于被删除结点的做子树的,所以将A子树放在左子树的最右边。
首先,我们让我们来看看delete函数。
/** * 进行删除 * @param key * @return 返回删除结点的value */ @Override public Value delete(Key key){ // 如果不包含key if (!containsNode(key)){ return null; } // preNode代表删除结点的父节点 Node node = root,preNode = root; int temp; while (true) { temp = node.key.compareTo(key); // 假如key小于结点的key,则转向左子树 if (temp > 0) { preNode = node; // 在删除的同时,将结点的N-- preNode.N --; node = node.left; } else if (temp < 0) { // 转向右子树 preNode.N --; preNode = node; node = node.right; } else { break; } } // 被删除结点的返回值 Value value = node.value; // mergeDelete代表合并删除 if (node == root){ root = mergeDelete(node); } // 假如删除的是父节点的左边的结点 else if (preNode.left!=null && preNode.left == node){ preNode.left = mergeDelete(node); }else { preNode.right = mergeDelete(node); } return value; }接下来是mergeDelete函数,代码的注释已经写的很清楚了,如果能够理解合并删除的原理,那么理解下面的代码也将轻而易举:
/** * 使用合并删除 * @param node * @return 返回的结点为已经进行删除后新的结点 */ public Node mergeDelete(Node node){ // 假如没有右子树 if (node.right == null){ return node.left; } // 假如没有左子树 else if (node.left == null){ return node.right; } // 既有右子树也有左子树 else { Node tempNode = node.left; // 转向左子树中最右边的结点 while (tempNode.right != null){ tempNode= tempNode.right; tempNode.N += size(node.right); } // 将删除结点的右子树放入正确的位置 tempNode.right = node.right; node.left.N += size(node.right); return node.left; } }归并删除有一个很大的缺点,那就是删除结点会导致树的高度的增加。接下来让我们来看看复制删除是怎么解决这个问题的。
复制删除(拷贝删除)
在说复制删除之前,我们需要先熟悉二叉查找树的前驱和后继(根据中序遍历衍生出来的概念)。
- 前驱:A结点的前驱是其左子树中最右侧结点。
- 后继:A结点的后继是其右子树中最左侧结点。
那么复制删除的原理是什么样的呢?很简,使用删除结点的前驱或者后继代替被删除的结点即可。
以下图来讲一下复制删除的原理(图源)
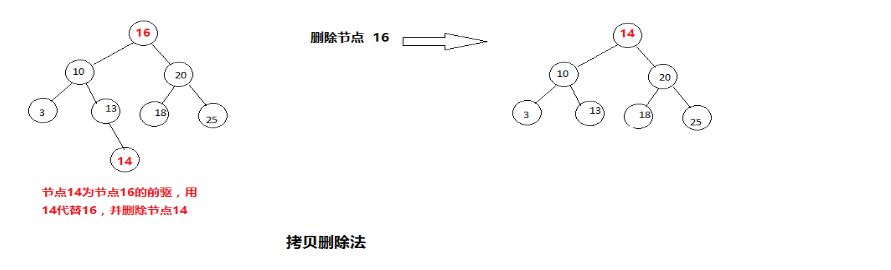
16结点的前驱为14结点,后驱为18结点,假如我们要删除16结点,即可将14结点或者18结点替代16即可。
/**
* 使用复制删除
* @param node 被删除的结点
*/
private Node copyDelete(Node node){
if (node.right == null){
return node.left;
}else if(node.left == null){
return node.right;
}
// 既有左子树又有右子树
else {
Node tempNode = node.left;
while(tempNode.right != null){
tempNode.N --;
tempNode = tempNode.right;
}
tempNode.right = node.right;
tempNode.left = (node.left==tempNode?tempNode.left:node.left);
tempNode.N = size(tempNode.left) + size(tempNode.right)+1;
return tempNode;
}
}
// 调用删除函数
public Value deleteByCopy(Key key){
// 如果不包含key
if (!containsNode(key)){
return null;
}
Node node = root;
Node preNode = node;
int temp;
while (true){
node.N --;
temp = node.key.compareTo(key);
// 假如key小于结点的key,则转向左子树
if (temp > 0) {
preNode = node;
node = node.left;
} else if (temp < 0) { // 转向右子树
preNode = node;
node = node.right;
} else {
break;
}
}
// 被删除结点的返回值
Value value = node.value;
if (node == root){
root = copyDelete(node);
}
// 假如删除的是父节点的左边的结点
else if (preNode.left!=null && preNode.left == node){
preNode.left = copyDelete(node);
}else {
preNode.right = copyDelete(node);
}
return value;
}在前面的代码中,我们总是删除node中的前驱结点,这样必然会降低左子树的高度,在前面中我们知道,我们也可以使用后继结点来代替被删除的结点。所以我们可以交替的使用前驱和后继来代替被删除的结点。
J.Culberson从理论证实了使用非对称删除,IPL的期望值是O(n√n),平均查找时间为(O(√n)),而使用对称删除,IPL的期望值为(nlgn),平均查找时间为O(lgn)。
性能分析:
| 二叉查找树 | 插入 | 删除 | 查找 | 空间 |
|---|---|---|---|---|
| 复杂度(平均) | O(lgn) | O(lgn) | O(lgn) | O(n) |
| 复杂度(最坏) | O(n) | O(n) | O(n) | O(n) |
尽管树已经很优秀了,但是我们我们可以想一想,如果我在put的操作的时候,假如使用的是顺序的put(e也就是按顺序的插入1,2,3,4……),那么树还是树吗?此时的树不再是树,而是变成了链表,而时间复杂度也不再是O(lgn)了,而是变成了O(n)。 接下来我们将介绍树中的2-3查找树和红黑树。
2-3 查找树
定义(来源:wiki)
2–3树是一种树型数据结构,内部节点(存在子节点的节点)要么有2个孩子和1个数据元素,要么有3个孩子和2个数据元素,叶子节点没有孩子,并且有1个或2个数据元素。


-
定义
如果一个内部节点拥有一个数据元素、两个子节点,则此节点为2节点。
如果一个内部节点拥有两个数据元素、三个子节点,则此节点为3节点。
当且仅当以下叙述中有一条成立时,T为2–3树:
- T为空。即T不包含任何节点。
- T为拥有数据元素a的2节点。若T的左孩子为L、右孩子为R,则
- L和R是等高的非空2–3树;
- a大于L中的所有数据元素;
- a小于等于R中的所有数据元素。
- T为拥有数据元素a和b的3节点,其中a < b。若T的左孩子为L、中孩子为M、右孩子为R,则
- L、M、和R是等高的非空2–3树;
- a大于L中的所有数据元素,并且小于等于M中的所有数据元素;
- b大于M中的所有数据元素,并且小于等于R中的所有数据元素。
首先我们说一下查找
2-3查找树的查找和二叉树很类似,无非就是进行比较然后选择下一个查找的方向。

2-3a查找树的插入
我们可以思考一下,为什么要两个结点。在前面可以知道,二叉查找树变成链表的原因就是因为新插入的结点没有选择的”权利”,当我们插入一个元素的时候,实际上它的位置已经确定了, 我们并不能对它进行操作。那么2-3查找树是怎么做到赋予“权利”的呢?秘密便是这个多出来结点,他可以缓存新插入的结点。(具体我们将在插入的时候讲)
前面我们知道,2-3查找树分为2结点和3结点,so,插入就分为了2结点插入和3结点插入。
**2-结点插入:**向2-结点插入一个新的结点和向而插入插入一个结点很类似,但是我们并不是将结点“吊”在结点的末尾,因为这样就没办法保持树的平衡。我们可以将2-结点替换成3-结点即可,将其中的键插入这个3-结点即可。(相当于缓存了这个结点)

**3-结点插入:**3结点插入比较麻烦,emm可以说是特别麻烦,它分为3种情况。
-
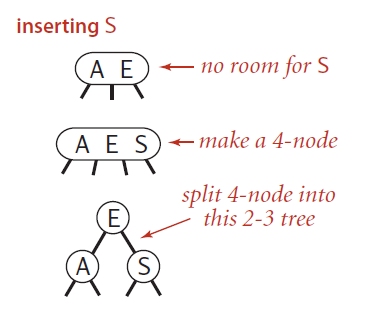
向一棵只含有3-结点的树插入新键。
假如2-3树只有一个3-结点,那么当我们插入一个新的结点的时候,我们先假设结点变成了4-结点,然后使得中间的结点为根结点,左边的结点为其左结点,右边的结点为其右结点,然后构成一棵2-3树,树的高度加1。
-
向父结点为2-结点的3-结点中插入新键。
和上面的情况类似,我们将新的节点插入3-结点使之成为4-结点,然后将结点中的中间结点”升“到其父节点(2-结点)中的合适的位置,使其父节点成为一个3-节点,然后将左右节点分别挂在这个3-结点的恰当位置,树的高度不发生改变

3. 向父节点为3-结点的3-结点中插入新键。
这种情况有点类似递归:当我们的结点为3-结点的时候,我们插入新的结点会将中间的元素”升“父节点,然后父节点为4-结点,右将中间的结点”升“到其父结点的父结点,……如此进行递归操作,直到遇到的结点不再是3-结点。

接下来就是最难的操作来了,实现这个算法,2-3查找树的算法比较麻烦,所以我们不得不将问题分割,分割求解能将问题变得简单。参考博客
首先我们定义数据结构,作用在注释已经写的很清楚了。
public class Tree23<Key extends Comparable<Key>,Value> {
/**
* 保存key和value的键值对
* @param <Key>
* @param <Value>
*/
private class Data<Key extends Comparable<Key>,Value>{
private Key key;
private Value value;
public Data(Key key, Value value) {
this.key = key;
this.value = value;
}
public void displayData(){
System.out.println("/" + key+"---"+value);
}
}
/**
* 保存树结点的类
* @param <Key>
* @param <Value>
*/
private class Node23<Key extends Comparable<Key>,Value>{
public void displayNode() {
for(int i = 0; i < itemNum; i++){
itemDatas[i].displayData();
}
System.out.println("/");
}
private static final int N = 3;
// 该结点的父节点
private Node23 parent;
// 子节点,子节点有3个,分别是左子节点,中间子节点和右子节点
private Node23[] chirldNodes = new Node23[N];
// 代表结点保存的数据(为一个或者两个)
private Data[] itemDatas = new Data[N - 1];
// 结点保存的数据个数
private int itemNum = 0;
/**
* 判断是否是叶子结点
* @return
*/
private boolean isLeaf(){
// 假如不是叶子结点。必有左子树(可以想一想为什么?)
return chirldNodes[0] == null;
}
/**
* 判断结点储存数据是否满了
* (也就是是否存了两个键值对)
* @return
*/
private boolean isFull(){
return itemNum == N-1;
}
/**
* 返回该节点的父节点
* @return
*/
private Node23 getParent(){
return this.parent;
}
/**
* 将子节点连接
* @param index 连接的位置(左子树,中子树,还是右子树)
* @param child
*/
private void connectChild(int index,Node23 child){
chirldNodes[index] = child;
if (child != null){
child.parent = this;
}
}
/**
* 解除该节点和某个结点之间的连接
* @param index 解除链接的位置
* @return
*/
private Node23 disconnectChild(int index){
Node23 temp = chirldNodes[index];
chirldNodes[index] = null;
return temp;
}
/**
* 获取结点左或右的键值对
* @param index 0为左,1为右
* @return
*/
private Data getData(int index){
return itemDatas[index];
}
/**
* 获得某个位置的子树
* @param index 0为左指数,1为中子树,2为右子树
* @return
*/
private Node23 getChild(int index){
return chirldNodes[index];
}
/**
* @return 返回结点中键值对的数量,空则返回-1
*/
public int getItemNum(){
return itemNum;
}
/**
* 寻找key在结点的位置
* @param key
* @return 结点没有key则放回-1
*/
private int findItem(Key key){
for (int i = 0; i < itemNum; i++) {
if (itemDatas[i] == null){
break;
}else if (itemDatas[i].key.compareTo(key) == 0){
return i;
}
}
return -1;
}
/**
* 向结点插入键值对:前提是结点未满
* @param data
* @return 返回插入的位置 0或则1
*/
private int insertData(Data data){
itemNum ++;
for (int i = N -2; i >= 0 ; i--) {
if (itemDatas[i] == null){
continue;
}else{
if (data.key.compareTo(itemDatas[i].key)<0){
itemDatas[i+1] = itemDatas[i];
}else{
itemDatas[i+1] = data;
return i+1;
}
}
}
itemDatas[0] = data;
return 0;
}
/**
* 移除最后一个键值对(也就是有右边的键值对则移右边的,没有则移左边的)
* @return 返回被移除的键值对
*/
private Data removeItem(){
Data temp = itemDatas[itemNum - 1];
itemDatas[itemNum - 1] = null;
itemNum --;
return temp;
}
}
/**
* 根节点
*/
private Node23 root = new Node23();
……接下来就是一堆方法了
}主要是两个方法:find查找方法和Insert插入方法:看注释
/**
*查找含有key的键值对
* @param key
* @return 返回键值对中的value
*/
public Value find(Key key) {
Node23 curNode = root;
int childNum;
while (true) {
if ((childNum = curNode.findItem(key)) != -1) {
return (Value) curNode.itemDatas[childNum].value;
}
// 假如到了叶子节点还没有找到,则树中不包含key
else if (curNode.isLeaf()) {
return null;
} else {
curNode = getNextChild(curNode,key);
}
}
}
/**
* 在key的条件下获得结点的子节点(可能为左子结点,中间子节点,右子节点)
* @param node
* @param key
* @return 返回子节点,若结点包含key,则返回传参结点
*/
private Node23 getNextChild(Node23 node,Key key){
for (int i = 0; i < node.getItemNum(); i++) {
if (node.getData(i).key.compareTo(key)>0){
return node.getChild(i);
}
else if (node.getData(i).key.compareTo(key) == 0){
return node;
}
}
return node.getChild(node.getItemNum());
}
/**
* 最重要的插入函数
* @param key
* @param value
*/
public void insert(Key key,Value value){
Data data = new Data(key,value);
Node23 curNode = root;
// 一直找到叶节点
while(true){
if (curNode.isLeaf()){
break;
}else{
curNode = getNextChild(curNode,key);
for (int i = 0; i < curNode.getItemNum(); i++) {
// 假如key在node中则进行更新
if (curNode.getData(i).key.compareTo(key) == 0){
curNode.getData(i).value =value;
return;
}
}
}
}
// 若插入key的结点已经满了,即3-结点插入
if (curNode.isFull()){
split(curNode,data);
}
// 2-结点插入
else {
// 直接插入即可
curNode.insertData(data);
}
}
/**
* 这个函数是裂变函数,主要是裂变结点。
* 这个函数有点复杂,我们要把握住原理就好了
* @param node 被裂变的结点
* @param data 要被保存的键值对
*/
private void split(Node23 node, Data data) {
Node23 parent = node.getParent();
// newNode用来保存最大的键值对
Node23 newNode = new Node23();
// newNode2用来保存中间key的键值对
Node23 newNode2 = new Node23();
Data mid;
if (data.key.compareTo(node.getData(0).key)<0){
newNode.insertData(node.removeItem());
mid = node.removeItem();
node.insertData(data);
}else if (data.key.compareTo(node.getData(1).key)<0){
newNode.insertData(node.removeItem());
mid = data;
}else{
mid = node.removeItem();
newNode.insertData(data);
}
if (node == root){
root = newNode2;
}
/**
* 将newNode2和node以及newNode连接起来
* 其中node连接到newNode2的左子树,newNode
* 连接到newNode2的右子树
*/
newNode2.insertData(mid);
newNode2.connectChild(0,node);
newNode2.connectChild(1,newNode);
/**
* 将结点的父节点和newNode2结点连接起来
*/
connectNode(parent,newNode2);
}
/**
* 链接node和parent
* @param parent
* @param node node中只含有一个键值对结点
*/
private void connectNode(Node23 parent, Node23 node) {
Data data = node.getData(0);
if (node == root){
return;
}
// 假如父节点为3-结点
if (parent.isFull()){
// 爷爷结点(爷爷救葫芦娃)
Node23 gParent = parent.getParent();
Node23 newNode = new Node23();
Node23 temp1,temp2;
Data itemData;
if (data.key.compareTo(parent.getData(0).key)<0){
temp1 = parent.disconnectChild(1);
temp2 = parent.disconnectChild(2);
newNode.connectChild(0,temp1);
newNode.connectChild(1,temp2);
newNode.insertData(parent.removeItem());
itemData = parent.removeItem();
parent.insertData(itemData);
parent.connectChild(0,node);
parent.connectChild(1,newNode);
}else if(data.key.compareTo(parent.getData(1).key)<0){
temp1 = parent.disconnectChild(0);
temp2 = parent.disconnectChild(2);
Node23 tempNode = new Node23();
newNode.insertData(parent.removeItem());
newNode.connectChild(0,newNode.disconnectChild(1));
newNode.connectChild(1,temp2);
tempNode.insertData(parent.removeItem());
tempNode.connectChild(0,temp1);
tempNode.connectChild(1,node.disconnectChild(0));
parent.insertData(node.removeItem());
parent.connectChild(0,tempNode);
parent.connectChild(1,newNode);
} else{
itemData = parent.removeItem();
newNode.insertData(parent.removeItem());
newNode.connectChild(0,parent.disconnectChild(0));
newNode.connectChild(1,parent.disconnectChild(1));
parent.disconnectChild(2);
parent.insertData(itemData);
parent.connectChild(0,newNode);
parent.connectChild(1,node);
}
// 进行递归
connectNode(gParent,parent);
}
// 假如父节点为2结点
else{
if (data.key.compareTo(parent.getData(0).key)<0){
Node23 tempNode = parent.disconnectChild(1);
parent.connectChild(0,node.disconnectChild(0));
parent.connectChild(1,node.disconnectChild(1));
parent.connectChild(2,tempNode);
}else{
parent.connectChild(1,node.disconnectChild(0));
parent.connectChild(2,node.disconnectChild(1));
}
parent.insertData(node.getData(0));
}
}
2-3树的查找效率与树的高度相关,这个可以很简单的理解,因为2-3树是平衡树,所以即使是最坏的情况下,它然仍是一棵树,不会产生类似链表的情况。
- 最坏情况:全是2-结点,树的高度最大,查找效率为lgN。
- 最好情况:全是3-结点,树的高度最小,查找效率为log3(N),约等于0.631lgN。
2-3查找树的原理很简单,甚至说代码实现起来难度都不是很大,但是却很繁琐,因为它有很多种情况,结束完欲仙欲死的2-3查找树,接下来让我们来好好的研究一下红黑树。
| 二叉查找树 | 插入 | 删除 | 查找 | 空间 |
|---|---|---|---|---|
| 复杂度(最好) | O(0.631lgN) | O(0.631lgN) | O(0.631lgN) | O(n) |
| 复杂度(最坏) | O(lgN) | O(lgN) | O(lgN) | O(n) |
红黑树
如果大家能够很好的理解2-3查找树的工作流程,那么理解红黑树也会变得轻松。因为可以这样说,红黑树是2-3树的一种实现,大家可以看下图:

红黑二叉查找树背后的思想就是使用标准的二叉查找树(由二结点构成) 和一些额外的信息(替换3-结点)来表示2-3树, 那么额外的信息是什么呢?由图我们可以得出:
- 红链接将两个2-结点链接起来构成了一个3-结点。
- 黑链接则是一个2-3树中普通的链接。

红黑树的性质:
- 节点是红色或黑色。
- 根是黑色。
- 所有叶子结点都是黑色(叶子是NIL节点)。
- 每个红色节点必须有两个黑色的子节点。(从每个叶子到根的所有路径上不能有两个连续的红色节点。)
- 从任一节点到其每个叶子的所有简单路径都包含相同数目的黑色节点。
我们可以想一想这些性质具体能够带来什么样的效果。
- 从根到叶子的最长距离不会大于最短距离的两倍长。(由第4条和第5条性质保证)这样就保证了树的平衡性。
由图我们可以知道。要判断一个是红还是黑,可以由指向该节点的链接判断出来。所以我们设置一个变量color,当链接为红时,变量为true,为黑时,变量color为false。(例如:若父节点指向该节点的链接为红色,则color为true)
其中我们约定空链接为黑色,根节点也为黑色,当插入一个结点的时候,设置结点的初始color为RED。
那么此时我们就可以来定义数据结构了。
public class RBTree<Key extends Comparable<Key>,Value> {
private static final boolean RED = true;
private static final boolean BLACK = false;
private class Node<Key extends Comparable<Key>,Value>{
private Key key;
private Value value;
private boolean color;
private Node rightNode,leftNode;
// 这棵子树中结点的个数,包括该节点
private int N;
private Node root;
public Node(Key key, Value value, boolean color, int n) {
this.key = key;
this.value = value;
this.color = color;
N = n;
}
}
/**
* 获得改结点与其父节点之间链接的颜色
* @param node
* @return
*/
private boolean isRed(Node node){
if (node == null){
return false;
}
return node.color;
}
……其他方法
}接下來我们先说一下红黑树的3个经典变换(左旋转,右旋转,颜色变换), 这些操作都是为了保持红黑的性质。
左旋的动画(图源)如图所示:(其中,在最上面的那根灰色的链接可红可黑)

有动态图后,实现Java就特别简单了,其中h,x和gif中的h,x相对应。
/**
* 左旋转
* @param h
* @return 返回根节点
*/
private Node rotateLeft(Node h) {
Node x = h.rightNode;
h.rightNode = x.leftNode;
x.leftNode = h;
x.color = h.color;
h.color = RED;
x.N = h.N;
h.N = size(h.leftNode)+size(h.rightNode)+1;
return x;
}有左旋转当然有右旋转,下面是右旋转的gif图片。

/**
* 右旋转
* @param h
* @return 返回根节点
*/
private Node rotateRight(Node h) {
Node x = h.leftNode;
h.leftNode = x.rightNode;
x.rightNode = h;
x.color = h.color;
h.color = RED;
x.N = h.N;
h.N = size(h.leftNode)+size(h.rightNode)+1;
return x;
}有前面的定义我们知道没有任何一个结点同时和两条红链接相连接,那么出现了我们该怎么办呢?进行颜色转换即可。


/**
* 颜色转换
* @param h
*/
private void changeColor(Node h){
h.color = !h.color;
h.leftNode.color = !h.leftNode.color;
h.rightNode.color = h.rightNode.color;
}在准备好这些操作后,我们就可以来正式的谈一谈put函数了。由前面的2-3 树我们知道2-3树的插入分为了很多种情况,既然红黑树是2-3树的一种实现,毋庸置疑,红黑树的插入情况也分为多种:2-结点插入(根节点,叶子结点),3-结点插入。
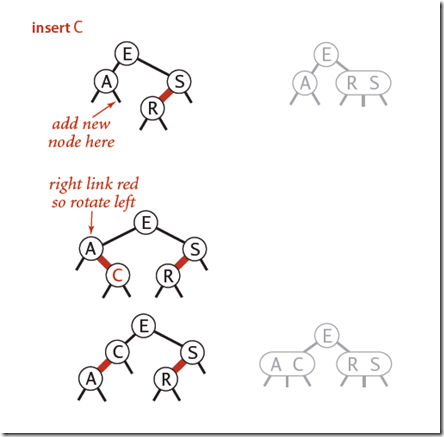
2-结点插入:2-结点插入实际上就是其父节点没有红链接与之相连接
-
根结点插入(向左插入和向右插入)

-
叶子结点插入
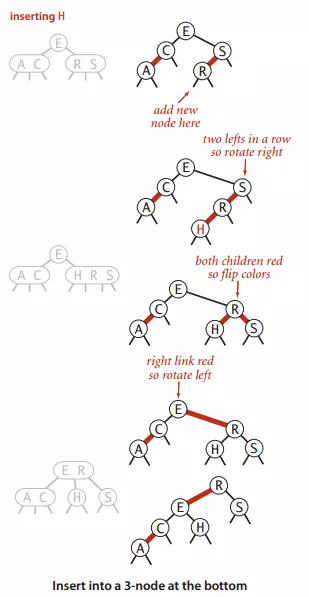
**3-结点插入:**也就是其父节点有一个红链接与之相连接。
-
一个3-结点插入
在下图中,分为了三种情况,larger(新键最大),smaller(新键最小),between(新键介于两者中间)

-
向树底部插入
那么我们该什么时候使用左旋转和右旋转呢?下面有几条规律
- 若右子节点为红色而左子节点为黑色,则左旋转
- 若左子节点为红色且左子节点的左子节点也为红色则右旋转
- 左右结点都为红色,则颜色转换
下面有一张转换关系图片。

有了这些转换关系图片我们写插入函数也就比较轻松了。
插入算法Java代码:
/**
* 红黑树的插入
* @param key
* @param value
*/
public void put(Key key,Value value){
if(key == null){
return ;
}
root = put(root,key,value);
// 进行颜色变换会将本身结点变红,而根节点必须保持黑色
root.color = BLACK;
}
/**
* 插入操作进行递归调用
* @param h
* @param key
* @param value
* @return
*/
private Node put(Node h, Key key, Value value) {
// 当h为叶子结点的左子树或者右子树
if (h == null){
return new Node(key,value,RED,1);
}
// 假如key小于结点的key,就转向左结点
if (key.compareTo(h.key)<0){
h.leftNode = put(h.leftNode,key,value);
}
// 转向右结点
else if (key.compareTo(h.key)>0){
h.rightNode = put(h.rightNode,key,value);
}
// 更新
else{
h.value = value;
}
// 若左边结点是黑色,右边结点是红色,则左旋转
if (isRed(h.rightNode) && !isRed(h.leftNode)){
h = rotateLeft(h);
}
// 若左子节点为红色且左子节点的左子节点也为红色则右旋转
if (isRed(h.leftNode) && isRed(h.leftNode.leftNode)){
h = rotateRight(h);
}
// 左右结点都为红色,则颜色转换
if (isRed(h.leftNode) && isRed(h.rightNode)){
changeColor(h);
}
h.N = size(h.leftNode)+size(h.rightNode) + 1;
return h;
}该段插入算法来自《算法(第四版)》。
接下来我们可以来说一说红黑树中另外一个比较难的操作:删除。删除这个操作不难,难的是我们如何在删除后任然保持红黑树的性质,这个问题才是难点。
在说删除之前我们可以回忆下前面的查找二叉树的删除中的复制删除方法,我们使用前驱后者后继的key和value来替代被删除的结点【注意:只有key和value互换,颜色不变】,那么如果我们在红黑树中也使用复制删除这种算法是不是能够把问题变得简单呢?当我们把删除的结点转移到前驱或者后继的时候,那么问题就变成了删除红色的叶子结点和删除黑色的叶子结点【注意:改叶子结点指的不是NULL(NIL)结点】。
因此我们可以很简单的将问题分成两类:
- 删除红色叶子结点
- 删除黑色叶子结点
删除红色叶子结点:
删除红色的叶子结点并没有什么好说的,直接删除,因为删除红色的叶子结点并不会影响破坏红黑树的平衡。因为我们知道一个红色结点绝对不可能存在只有左结点或者只有右结点的情况(可以解释下:若存在左子结点或右子结点,则子节点绝对会是黑色的,那么则会违反“从任一节点到其每个叶子的所有简单路径都包含相同数目的黑色节点”这个性质)
如下图(图源),就是不符合性质5,因为左边结点和右边结点到根节点的经过的黑色结点的数量相差一。

删除黑色叶子结点:
删除黑色结点有个很大的问题,那就是会破坏从任一节点到其每个叶子的所有简单路径都包含相同数目的黑色节点这个性质,所以我们不得不对黑色结点的删除做一下考虑。对此我们又可以分两个方面来考虑:
- 删除的黑色结点只有左子结点或者右子结点
- 删除的黑色结点没有子结点
-
删除的黑色结点只有左子结点或者右子结点
前面我们知道,我们使用的是前驱或者后继结点来替代被删除的结点,那么被删除的结点只最多只有一个子节点。并且由于红黑树的性质我们知道情况只能为以下两种情况(可以想下为什么结点不能为黑色):

前驱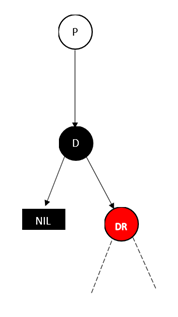
对于这种,我们只需要将被删除黑结点的子节点替代被删除的结点即可,并将颜色改为black即可。
-
删除的黑色结点没有子结点
这种情况是最复杂的,so,让我们来好好聊一聊这个东东。
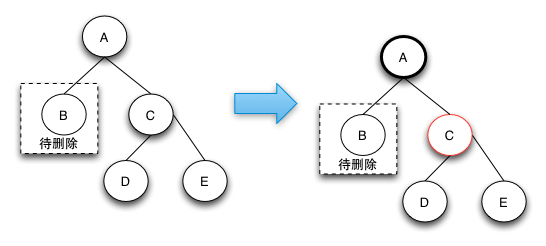
2.1 待删除的节点的兄弟节点是红色的节点。
因为删除的结点的兄弟结点是红色结点,我们进行左旋转,如图所示,我们可以发现红黑树的性质并没有被破害。
当然如果B结点在右边,我们使用右旋转就好了。这个时候情况就变成了下面
2.2的那种情况。图片来源美团技术团队

2.2 待删除的节点的兄弟节点是黑色的节点,且兄弟节点的子节点都是黑色的。
下面的这幅图我纠结了很久,当时我看的时候,我一直在纠结为什么红黑树会出现下面的这种情况,因为它明显不符合红黑树的性质。我认为是博主搞错了,后来我又去看了圣书《算法导论》也是这样的,就更加的坚信是我想错了。
在这里我说下自己的理解:
在下面的图中,DE结点不一定是有数据的结点,也可能为NULL结点(NULL结点也是黑色的,这是我们的规定),如果为NULL结点,那么这种情况就回到了上图中的情况,B的兄弟结点D为黑色。 我们按照下图的操作,然后将D结点变成红色。在将B结点删除后,这个时候我们很容易的知道A结点的兄弟结点和A结点绝对不平衡了(违反了性质5),这个时候我们将B结点看成A结点以及它的子树C结点就看成A结点的兄弟结点。(这便是一个递归操作)
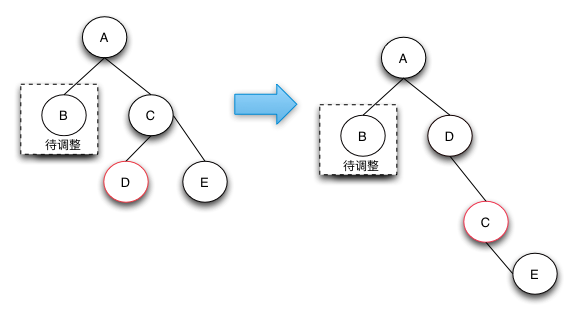
2.3 待调整的节点的兄弟节点是黑色的节点,且兄弟节点的左子节点是红色的,右节点是黑色的(兄弟节点在右边),如果兄弟节点在左边的话,就是兄弟节点的右子节点是红色的,左节点是黑色的。
这种状态我们可以理解为D是一棵左子树,E是一棵右子树,这样理解的话树还是可以保持平衡的。不过在*美团技术团队*上面说“他是通过case 2(也就是2.2操作)操作完后向上回溯出现的状态”,不过我没画出这幅图。
在这种情况下我们可以这样理解:
在B子树中已经缺失了一个黑结点,那么我们必须要在D子树中和E子树中,让他们也损失一个黑结点(这个不像2.1我们直接将兄弟变红就行了,因为该节点的左结点为红结点),so,我们先将结点左旋转,得到2.4的情况
2.4 待调整的节点的兄弟节点是黑色的节点,且右子节点是是红色的(兄弟节点在右边),如果兄弟节点在左边,则就是对应的就是左节点是红色的。
关于这个我们可以这样理解:
我们将D结点变红后,那边右边就要两个连续的红色结点了,so,我们需要左旋转,同时A结点变红。这样右边的结点就少了一个黑色的结点。树局部平衡

这里有一个《算法第四版》关于红黑树的参考资料。我会根据算法的思路逐个解决问题。
首先,我们可以想一想,当我们删除一个结点的时候会进行一些操作,但是我们必须得保证黑链的平衡,这个时候我们就要根据一些规则来平衡树:
- 若右子节点为红色而左子节点为黑色,则左旋转
- 若左子节点为红色且左子节点的左子节点也为红色则右旋转
- 左右结点都为红色,则颜色转换
让我们来写一个修复函数吧:
/**
* 平衡树
* @param h
* @return
*/
private Node fixUp(Node h){
if (isRed(h.rightNode)){
h = rotateLeft(h);
}
if (isRed(h.leftNode) && isRed(h.leftNode.leftNode)){
h = rotateRight(h);
}
if (isRed(h.leftNode) && isRed(h.rightNode)){
changeColor(h);
}
h.N = size(h.leftNode)+size(h.rightNode)+1;
return h;
}有了这个函数,接下来让我们实现一个删除最大值的函数:
在前面我们知道删除一个红结点直接删除就行了,所以如果被删除的结点附近有红结点,然后直接进行删除岂不是美滋滋!!

这个步骤很简单,就是将红色的结点移动到最右边:
/**
* 将红色结点移动到右边
* @param h
* @return
*/
private Node moveRedRight(Node h){
changeColor(h);
// 假如结点的左结点的左结点为红色结点
if (isRed(h.leftNode.leftNode)){
// 进行右转
h = rotateRight(h);
// 然后改颜色
changeColor(h);
}
return h;
}接下来我们就可以进行删除最大元素了:
public void deleteMax(){
if (root == null){
return;
}
if (!isRed(root.leftNode) && !isRed(root.rightNode)) {
root.color = RED;
}
root = deleteMax(root);
// 删除之后root不为空,则将root的颜色变为黑色
if (root != null){
root.color = BLACK;
}
}
private Node deleteMax(Node h) {
// 假如结点的左边是红色结点,则进行右旋转
if (isRed(h.leftNode)){
h = rotateRight(h);
}
// 如果右边为空的,则代表以及达到最大的结点
if (h.rightNode == null){
return null;
}
// 假如结点的右子节点为是黑色,右子节点的左子节点是黑色
// 在这种情况下,我们进行右旋转没办法得到将红色的结点转到右边来
// 所以我们执行moveRedRight并在里面创造红色的结点
if (!isRed(h.rightNode) && !isRed(h.rightNode.leftNode)){
h = moveRedRight(h);
}
h.rightNode = deleteMax(h.rightNode);
return fixUp(h);
}下面是一个关于删除最大值的例子:
既然我们能够删除最大值,那么也就能够删除最小值,删除最小值就是将红色的结点移动到左边:

/**
* 将红色结点移动到左边
* @param h
* @return
*/
private Node moveRedLeft(Node h){
changeColor(h);
if (isRed(h.rightNode.leftNode)){
h.rightNode = rotateLeft(h.rightNode);
h = rotateLeft(h);
changeColor(h);
}
return h;
}然后是删除最小值的算法
public void deleteMin(){
if (root == null){
return;
}
if (!isRed(root.leftNode) && !isRed(root.rightNode)) {
root.color = RED;
}
root = deleteMin(root);
if (root != null){
root.color = BLACK;
}
}
private Node deleteMin(Node h) {
if (h.leftNode == null) {
return null;
}
if (!isRed(h.leftNode) && !isRed(h.leftNode.leftNode)){
h = moveRedLeft(h);
}
h.leftNode = deleteMin(h.leftNode);
return fixUp(h);
}上面的删除最大和删除最小值的操作总结起来就是:我希望我删除的结点是红色的结点,如果不是红色的结点,那么我就去借红色的结点。以删除最大值为例,我希望h的右子结点为红色结点,如果没有怎么办?那么我们就去左子节点的左边拿(也就是进行右旋转-这样可以保证h的下一个结点为红色),如果左子节点为黑色。但是h的右子节点为的左子节点为红色,我们就可以安安心心的向右子节点移了,因为我们可以保证右子节点的右子节点为红结点(通过右旋转),如果不是怎么办?创造就行了。
说完这么多,我们终于可以来说说删除操作了:
public void delete(Key key){
if (key == null){
return;
}
// 首先将结点变红以便于操作
if (!isRed(root.leftNode) && !isRed(root.rightNode)) {
root.color = RED;
}
root = delete(root,key);
if (root != null){
root.color = BLACK;
}
}
private Node delete(Node h, Key key) {
if (key.compareTo(h.key)<0){
if (!isRed(h.leftNode) && !isRed(h.leftNode.leftNode)){
h = moveRedLeft(h);
}
h.leftNode = delete(h.leftNode,key);
}
// 假如key比Node的key要大,或者相等
else{
// 左子节点为红色,则进行右旋转,这样能够将红色结点向右集中
if (isRed(h.leftNode)){
// 通过右转能够将红色结点上升
h = rotateRight(h);
}
// 这一步中,假如h的右结点为空,则h为叶子结点(此叶子结点并不代表NULL结点)
// 因为假如有左子节点的话,那么左子节点一定是红色(因为右子节点为空),那么在上面的一个if语句中h已经被右旋转到了右子节点
// 且h必定为红色的结点,这个时候我们就可以直接删除
if (key.compareTo(h.key) == 0 && h.rightNode == null){
return null;
}
if (!isRed(h.rightNode) && !isRed(h.rightNode.leftNode)){
h = moveRedRight(h);
}
if (key.compareTo(h.key) == 0){
// 找到h的后继结点,然后交换key和value,然后就可以删除最小节点了
Node x = min(h.rightNode);
h.key = x.key;
h.value = x.value;
h.rightNode = deleteMin(h.rightNode);
}
else{
h.rightNode = delete(h.rightNode,key);
}
}
return fixUp(h);
}
/**
* 找后继结点
* @param x
* @return
*/
private Node min(Node x) {
if (x.leftNode == null) {
return x;
}
else{
return min(x.leftNode);
}
}以上的来自来自于《算法第四版》,这个是官网的源代码。写的真好,简洁明了。我们可以根据这个源代码把自己的思路理一理,想一想为什么它要这样去写。
| 红黑树 | 插入 | 删除 | 查找 | 空间 |
|---|---|---|---|---|
| 复杂度 | O(lgN) | O(lgN) | O(lgN) | O(n) |
HASH大法好
散列表
散列表是一个比较简单的数据结构,但是却设计的很精妙,大家可以看看我写的关于Java中HashMap的源码分析。
散列表的思想很简单,就是将KEY通过数学方法转化为数组的索引,然后通过索引来访问数组中的值value。如果大家能够将那篇HashMap的源码分析看懂,那么这一小节的内容也轻而易举。

由上图我们知道,如何设置一个好的散列方法是算法中的很重要的一部分。总的来说,为一个数据结构实现一个优秀的散列方法需要满足3个条件。
- 一致性:等价的key必定要产生相等的散列值
- 高效性:计算简便
- 均匀性:均匀地散列所有的键
在HashMap的源码中,我们可以知道HashMap是使用拉链法(或者红黑树)来解决hash冲突的。实际上我们还有一种方法,叫做开放地址散列表,我们使用大小为M的数组来保存N个键值对(M>N),通过依靠数组中的空位来解决碰撞冲突。
开放地址散列表中最简单的方法叫做线性探测法:当碰撞发生时(也就是数组中该散列值的位置已经存在一个键了),我们就直接检查散列表中的下一个位置(将索引值+1)。so,我们可以来写一下代码实现它。
我们可以先将插入,查找写完
public class LinearHashST<Key extends Comparable<Key>,Value> {
private Key[] keys;
private Value[] values;
/**
* 键值对的数量
*/
private int N;
/**
* 默认数组大小
*/
private int M = 16;
public LinearHashST() {
keys = (Key[]) new Object[M];
values = (Value[]) new Object[M];
}
/**
* 初始化容量
* @param N 指令数组大小
*/
public LinearHashST(int N) {
M = N;
keys = (Key[]) new Object[M];
values = (Value[]) new Object[M];
}
private int hash(Key key){
return (key.hashCode()&0x7fffffff)%M;
}
public void put(Key key,Value value){
// 如果容量达到阀值,则扩容
if (N>=M*0.8){
resize(M*2);
}
// 得到hash值
int h;
for (h = hash(key);keys[h]!=null;h = (h+1)%M){
// key相等则更新
if (key.compareTo(keys[h]) == 0){
values[h] = value;
return;
}
}
keys[h] = key;
values[h] = value;
N ++;
}
public Value get(Key key){
int h;
for (h = hash(key);keys[h]!=null;h=(h+1)%M){
if (key.compareTo(keys[h]) == 0){
return values[h];
}
}
return null;
}
}接下来我们来说说删除操作:
操作操作我们仅仅就是就是将位置上面的key和value变成null吗?不,当然不是。我们举个例子(其中S和C是同一个hash值2,也就是他们是产生了hash冲突,假如我们删除了S并把它置为NULL):
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| A | S | Z | C | D | F | V | G | ||
| A | NULL | Z | C | D | F | V | G |
我们这个时候可以用get算法看一看,看看是否能够找到C。是不是发现我们并不能够找到C。这时候可能有人会有疑问,我全部循环一遍,不就ok了吗?但是,如果这样操作我们是不是就失去了散列表的查找时间复杂度的优势了呢?
让我们来看一看散列表的delete操作,当我们删除某个位置上面的键值对时,我们就需要将被删除位置上面的坑填好。哪么哪些元素回来填这个坑呢?1. 本身hash值为这个位置的键值对,但是因为这个“坑”被占了而不得不下移一位的结点。2. hash值与被删除结点的hash值一样,所以它可能会有机会来补这个“坑”位
/**
* 进行删除操作
* @param key
*/
public void delete(Key key){
int h = hash(key);
while(keys[h]!=null){
// 假如key存在
if (keys[h].compareTo(key) == 0){
keys[h] = null;
values[h] = null;
// 键值对数量减1
N--;
for (h=(h+1)%M; keys[h] != null;h=(h+1)%M){
// 将被删除结点后面的重新排列一下
Key keyToRedo = keys[h];
Value valToRedo = values[h];
keys[h] = null;
values[h] = null;
// 之所以N--是因为在put操作中N++了
N--;
put(keyToRedo,valToRedo);
}
// 缩小容量
if (N>0 && N == M/8){
resize(M/2);
}
}
h = (h+1)%M;
}
return;
}接下来就是扩容操作了(耗时操作)
/**
* 进行改变容量操作
* @param cap 容量大小
*/
private void resize(int cap){
LinearHashST<Key,Value> linearHashST = new LinearHashST(cap);
for (int i=0;i<M;i++) {
if (keys[i] != null){
linearHashST.put(keys[i],values[i]);
}
}
keys = linearHashST.keys;
values = linearHashST.values;
M = linearHashST.M;
}| 线性探测法 | 插入 | 删除 | 查找 | 空间 | 扩容 |
|---|---|---|---|---|---|
| 复杂度 | O(1) | O(N) | O(1) | O(n) | O(n) |
写完这篇博客我是一个头两个大,写的快哭了同时也快吐了,有史以来写的最吃力的一篇博客,其中在红黑树的删除花了自己将近3天的时间。谁让我这么菜呢,我能怎么办,我也很无奈啊。




















【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· Linux系列:如何用heaptrack跟踪.NET程序的非托管内存泄露
· 开发者必知的日志记录最佳实践
· SQL Server 2025 AI相关能力初探
· Linux系列:如何用 C#调用 C方法造成内存泄露
· AI与.NET技术实操系列(二):开始使用ML.NET
· 被坑几百块钱后,我竟然真的恢复了删除的微信聊天记录!
· 没有Manus邀请码?试试免邀请码的MGX或者开源的OpenManus吧
· 【自荐】一款简洁、开源的在线白板工具 Drawnix
· 园子的第一款AI主题卫衣上架——"HELLO! HOW CAN I ASSIST YOU TODAY
· 无需6万激活码!GitHub神秘组织3小时极速复刻Manus,手把手教你使用OpenManus搭建本