相机模型——内参、外参

# 相机参数

针孔相机模型，包含四个坐标系：物理成像坐标系、像素坐标系、相机坐标系、世界坐标系。

相机参数包含：内参、外参、畸变参数

内参

【Intrinsics】

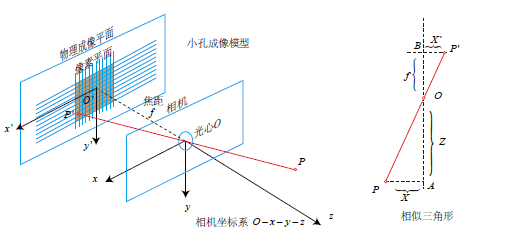
物理成像坐标系：\(O'-x'-y'\)

像素坐标系：\(O-u-v\)

相机坐标系：\(O-x-y\)

世界坐标系：\(O-X-Y-Z\)

在世界坐标系下的点\(P[X,Y,Z]^T\)，通过相机坐标系下的光心\(O\)投影到物理成像平面上的\(P'[X',Y',Z']^T\)，对应到像素坐标系下的\([u,v]^T\)。

由相似三角形可以得到：

\[\frac Z f = -\frac X {X'}=-\frac Y {Y'} \]

带负号是因为小孔成像成的是倒像。为了简化模型，可以把物理成像平面看作为放到了相机的前方，这样可以直观的认为成立的正像（虚像），就像下图：

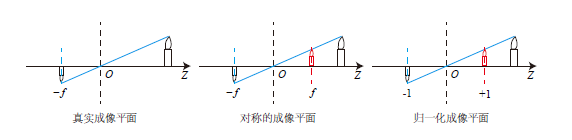
可以得到：

\[\begin{align} \frac Z f& = \frac X {X'}=\frac Y {Y'} \\ X'&=f\frac X Z \\ Y'&=f\frac Y Z \end{align} \]

从物理成像坐标系到像素坐标系之前，相差了一个缩放和平移。缩放是因为两个坐标系之前的表示的单位长度不一致，平移是因为两个坐标系的原点不一致。

假设，像素坐标在\(u\)方向上缩放了\(\alpha\)倍，在\(v\)方向上缩放了\(\beta\)倍，同时，原点平移了\([c_x,c_y]^T\)。那么点\(P'[X',Y',Z']^T\)与像素坐标系下\([u,v]^T\)的关系为：

\[\begin{cases} u&=\alpha X'+c_x \\ v&=\beta Y'+c_y \\ \end{cases} \\ \\ \Downarrow \\ f_x = \alpha f \\ f_y= \beta f \\ \Downarrow \\ \begin{cases} u&=f_x \frac XZ + c_x \\ v&=f_y \frac YZ + c_y \\ \end{cases} \\ \]

其中，变量的单位是\(f \rightarrow mm ; \alpha, \beta \rightarrow 像素/mm; f_x,f_y \rightarrow 像素\)。将坐标进行归一化，写成矩阵形式，并对左侧像素坐标进行齐次化，方便后面的运算：

\[\begin{bmatrix} u \\ v\\ 1 \\ \end{bmatrix} = \frac 1Z \begin{bmatrix} f_x &0 &c_x \\ 0 &f_y &c_y\\ 0 &0 &1 \\ \end{bmatrix} \overset{\triangle}{=} \frac1Z \boldsymbol {KP} \\ \Downarrow \\ Z\begin{bmatrix} u \\ v\\ 1 \\ \end{bmatrix} = \begin{bmatrix} f_x &0 &c_x \\ 0 &f_y &c_y\\ 0 &0 &1 \\ \end{bmatrix} \overset{\triangle}{=} \boldsymbol {KP} \\ \]

把中间的量组成的矩阵称为相机的内参矩阵（Camera Intrinsics）\(\boldsymbol K\)。

内参矩阵参数获取

图像大小\([w,h]\)，单位\(pixel\)；相机焦距\(f\)，单位\(mm\)；视场角\(FOV-\alpha\)，单位弧度；像素单元长度\(\mathrm{d}x,\mathrm{d}y\)，单位\(mm/pixel\)；内参\(f_x,f_x\)，单位\(pixel\)：

\[\boldsymbol{f_x=\frac f{\mathrm{d}x}}\\ \boldsymbol{f_y=\frac f{\mathrm{d}y}} \\ \boldsymbol{c_x=\frac w2} \ (假设相机主点在图像中央) \\ \boldsymbol{c_y =\frac h2} \ (假设相机主点在图像中央) \\ \]

\(\boldsymbol {f_x}\)就相当于用\(x\)方向的像素数去量化物理焦距\(f\)；

\(\boldsymbol {f_y}\)就相当于用\(y\)方向的像素数去量化物理焦距\(f\)；

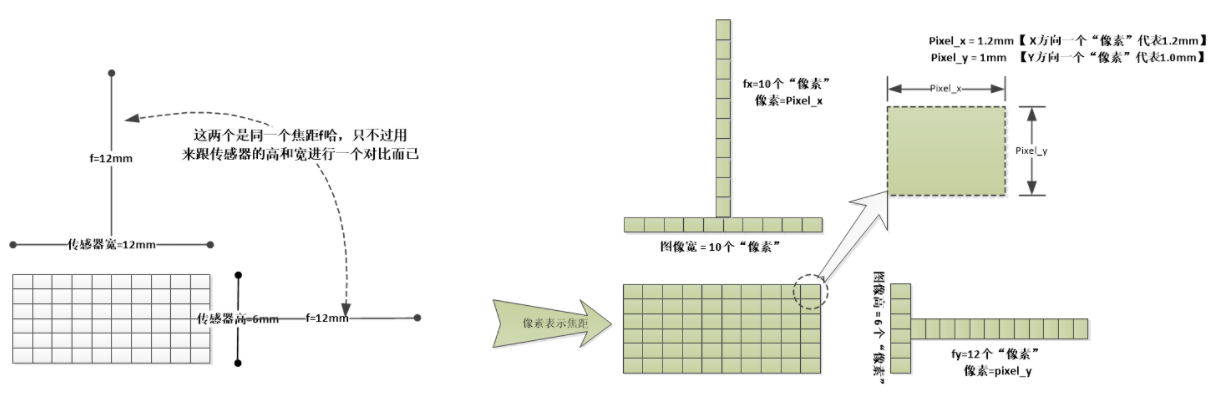
已知相机的硬件参数求内参

相机的内参出厂后就是固定不变的，如果知晓相机的出厂参数，可以计算相机的内参。

如成像传感器是\(m\times n(\mu m)\)，图像尺寸是\(w\times h(pixel)\)，那么图像像素单元就是

\[\mathrm{d}x=\frac mw(\mu m/pixel)\\ \mathrm{d}y=\frac nh(\mu m/pixel) \\ c_x=\frac w2 \\ c_y =\frac h2 \]

如果\(\mathrm{d}x=\mathrm{d}y\)，则图像像素单元是一个正方形，此时\(\boldsymbol {f_x=f_y}\)；

如果\(\mathrm{d}x \neq \mathrm{d}y\)，则图像像素单元是一个矩形，此时\(\boldsymbol {f_x \neq f_y}\)。

如成像传感器是\(2000\times 1000(\mu m)\)，图像尺寸是\(1000\times 500(pixel)\)，那么图像像素单元就是\(\mathrm{d}x=\mathrm{d}y=2(\mu m/pixel)\)，\(c_x=500,c_y=250(pixel)\)

求视场角FOV

这里只是求水平方向上的FOV，垂直方向上的FOV求法和水平是一致的。

其中，成像传感器是\(m\times n(\mu m)\)，图像尺寸是\(w\times h(pixel)\)，像素单元\(x\)轴方向长度\(\mathrm{d}x=\frac mw(\mu m/pixel)\)，可以看到：

\[\begin{align} \tan({\frac {\alpha}2} \cdot \frac {\pi}{180} ) &= \frac {m/2}{f} \\ &\Downarrow \\ FOV=\alpha &=2\arctan(\frac {m/2}{f}) \cdot \frac {180}{\pi} \label{fisst} \tag{1.1} \\ &\Downarrow \\ m &=w\cdot \mathrm{d}x \\ &\Downarrow \\ FOV=\alpha &=2\arctan(\frac {w\cdot \mathrm dx/2}{f}) \cdot \frac {180}{\pi} \\ &\Downarrow \\ f_x &= \frac f{\mathrm dx}\\ &\Downarrow \\ FOV=\alpha &=2\arctan(\frac {w}{2f_x}) \cdot \frac {180}{\pi} \label{second} \tag{1.2}\\ \end{align} \]

如果已知相机传感器尺寸，通过公式\(\ref{fisst}\)可以计算出相机的视场角\(FOV\)；

如果已知相机内参，通过公式\(\eqref{second}\)可以计算出相机的视场角\(FOV\)。

通过FOV计算内参

由公式\(\eqref{second}\)，可得：

\[\begin{align} \frac{w}{2f_x} &= \tan(\frac {FOV}{2} \cdot \frac {\pi}{180}) \\ &\Downarrow\\ f_x &= \frac w{2\tan(\frac {FOV}{2} \cdot \frac {\pi}{180})} \\ f_y &= \frac h{2\tan(\frac {FOV}{2} \cdot \frac {\pi}{180})} \end{align} \]

如果\(\mathrm{d}x=\mathrm{d}y\)，则图像像素单元是一个正方形，此时\(\boldsymbol {f_x=f_y}\)；\(\boldsymbol {c_x=\frac w2 }\)；\(\\ \boldsymbol {c_y =\frac h2}\)。

外参

【Extrinsics】

相机内参描述的是在相机坐标系下的点到像素坐标系下的对应关系，上文内提到的\(\boldsymbol P\)也是在相机坐标系下的点。相机在三维空间中运动，记点\(\boldsymbol P\)在世界坐标系下的点为\(\boldsymbol P_w\)，在相机坐标系下的坐标为\(\boldsymbol P_c\)。

相机在世界坐标系下的位姿，由相机的旋转矩阵\(\boldsymbol R\)和平移向量\(\boldsymbol t\)来描述。此时有：

\[Z\cdot \boldsymbol {P_{uv} |_{3\times1} }=Z \cdot \begin{bmatrix} u \\ v\\ 1\\ \end{bmatrix} =\boldsymbol{K} (\boldsymbol{RP_w+t})=\boldsymbol{K|_{3\times3} \cdot T|_{3\times4} \cdot P_w|_{4\times1}} \label{third} \tag{1.3} \]

两侧都是齐次坐标，同时因为齐次坐标乘上非零常数后表达同样的含义，所以可以简单地把Z去掉：

\[\boldsymbol {P_{uv}= KTP_w} \]
但这样等号意义就变了，成为在齐次坐标下相等的概念，相差了一个非零常数。为了避免麻烦，我们还是从传统意义下来定义书写等号。（《SLAM十四讲》）

式\(\ref {third}\)表明，我们可以把一个世界坐标点先转换到相机坐标系，再除掉它最后一维的数值（该点距离相机成像平面的深度），这就相当于把最后一维进行了归一化处理，得到点\(P\)在相机归一化平面上的投影：

\[\begin{align} (\boldsymbol {RP_w+t})= &\underbrace{[X,Y,Z]^T} & \to \ \ \ \ &\underbrace{[X/Z,Y/Z,1]^T} \\ &{ \ \ \ 相机坐标} & &{\ \ \ 归一化坐标} \end{align} \]

归一化坐标可以看成相机前方\(z=1\)处的平面上的一个点，这个\(z=1\)平面也称为归一化平面。归一化坐标左称内参\(\boldsymbol K\)就得到了像素坐标，因此可以把像素坐标\([u,v]^T\)看成对归一化平面上的点进行量化测量的结果。

同时可以看到，如果对相机坐标同时乘上任意非零常数，归一化坐标都是一样的，也就是点的深度信息在投影的过程中丢失了，所以在单目视觉中没法得到像素点的深度值。