关于样本方差以及样本协方差的一点思考

本篇文章主要讨论样本方差和样本协方差除以n-1问题，其他暂且不做过多赘述。

方差的维基百科定义：一个随机变量的方差描述的是它的离散程度，也就是该变量到其期望值的距离。

计算公式：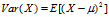

样本方差：样本方差是依据所给样本对方差做出的一个无偏估计。用样本去推测整体情况。

计算公式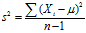： 其中n为样本数。

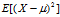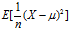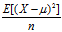等等，为什么样本方差的计算公式不是n而是n-1呢，不应该是求平均值吗，你看，假设一对数据的总体样本为：，然后每个样本不就是，也就是，这样似乎才是符合数学推理的吧？但是为什么那么多统计学家给出的却要除以n-1呢？

原来啊，我们在估算的时候总是用最大似然方法，让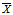去代替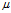，这样就会导致：

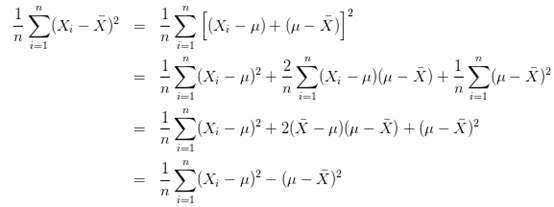
是不是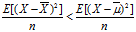：,那么这样的话，我们是不是总是莫名其妙的对样本方差估计小了？所以我们就要放大，就变成了除以n-1,那为什么不处以n-a，a为任意小于n的实数呢。这个挖个坑，因为我也没太明白，有没有知道的可以告诉我，哈哈。

还有为什么不能用均值代替期望呢，因为期望和均值相等只是理想情况下的，比如你扔硬币，次数越多，可能越有偏差。

刚刚那个是从数学上推断，我们来想想逻辑上的。

假设我们两个平均有8个苹果，我比平均值多1个，那么我就算不知道你的任何信息，我也会计算出你的信息吧，也就是说，这一部分信息是多余的，那假设还有一个小王，我是比平均多一个，小王是少一个，我根本不用知道你的信息，就可以知道你的苹果数，对吧。样本方差也是这样，我们用整体去推测个体，是不需要个体都知道的，缺失一个信息是没有影响的，所以我们要从总样本中减去1。

方差是协方差的特殊情况，就是当两个变量x与y相等时候的情况。既然我们已经知道样本方差为什么是除以n-1。那么样本协方差也是一样的道理。

样本协方差的计算公式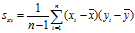：。