动态规划:求最长公共子序列和最长公共子串
最长公共子序列(LCS):
这同样是一道经典题目,定义就不说了。
为了方便说明,我们用Xi代表{x1,x2,‥xi},用Yj代表{y1,y2,‥yj}。那么,求长度分别为m,n的两个序列X,Y的LCS就相当于求Xm与Yn的LCS。我们将其分割为局部问题进行分析。
首先,求Xm与Yn的LCS要考虑一下两种情况。
Ⅰ.
xm=yn时,在Xm-1与Yn-1的LCS后面加上xm(=yn)就是Xm与Yn的LCS。
举个例子,X={a,b,c,c,d,a}, Y={a,b,c,b,a} 时xm=yn,所以在Xm-1与Yn-1的LCS({a,b,c} )后面加上 xm(=a)就是Xm与Yn的LCS。
Ⅱ.
xm≠yn时,Xm-1与Yn的LCS和Xm与Yn-1的LCS中更长的一方就是Xm与Yn的LCS。
举个例子,X={a,b,c,c,d,a}, Y={a,b,c,b,a} 时xm=yn,所以在Xm-1与Yn的LCS为{a,b,c} ,Xm-1与Yn的LCS为{a,b,c,b},因此Xm-1与Yn的LCS就是Xm与Yn的LCS。
定义:
c[i][j]:为Xi与Yj的LCS的长度。
于是c[i][j]的值可由一下递推关系求得:
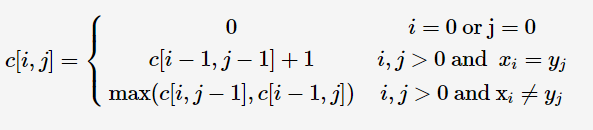
代码如下:
#include<bits/stdc++.h> using namespace std; const int maxn = 1000005; int dp[maxn][maxn]; int main() { string s1, s2; cin >> s1 >> s2; int a = s1.size(), b = s2.size(); for (int i = 0; i < a; i++) { for (int j = 0; j < b; j++) { if (s1[i] == s2[j]) dp[i + 1][j + 1] = dp[i][j] + 1; else dp[i + 1][j + 1] = max(dp[i][j + 1], dp[i + 1][j]); } } cout << dp[a][b]; return 0; }
最长公共子串:
字串要求是连续的子序列,根据上面子序列的递推公式,因此我们可以稍微改一下递推公式,得到如下的递推关系:
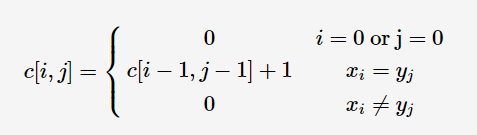
代码如下:
#include<bits/stdc++.h> using namespace std; const int maxn = 10005; int dp[maxn][maxn]; int main() { string s1, s2; cin >> s1 >> s2; int a = s1.size(), b = s2.size(); for (int i = 0; i < a; i++) { for (int j = 0; j < b; j++) { if (s1[i] == s2[j]) dp[i + 1][j + 1] = dp[i][j] + 1; else dp[i + 1][j + 1] = 0; } } cout << dp[a][b]; return 0; }
如果有什么不对的地方,欢迎大家指出哦(虽然知道没什么人看,但还是要说一下)。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号