Binary Indexed Tree
A Fenwick tree or binary indexed tree is a data structure that can efficiently update elements and calculate prefix sums in a table of numbers. It's actually an array rather than a real tree. Note that its index begins from 1 rather than 0.
Given an array arr[1...n], there are mainly two methods:
-
prefixSum(idx)
Compute the sum of the first i-th elements.
-
update(idx,delta)
Modify the value of a specified element of the array arr[i] = x
1.prefixSum
-
- Initialize the output sum as 0, the current index as x+1.
- Do following while the current index is greater than 0.
...a) Add BITree[index] to sum
...b) Go to the parent of BITree[index]. The parent can be obtained by removing
the last set bit from the current index, i.e., index = index - (index & (-index)) - Return sum.
-
int prefixSum(int idx) { idx += 1; int result = 0; while (idx > 0) { result += bitArr[idx]; idx = idx - (idx & -idx); } return result; }
2.update
-
- Initialize the current index as x+1.
- Do the following while the current index is smaller than or equal to n.
...a) Add the val to BITree[index]
...b) Go to parent of BITree[index]. The parent can be obtained by incrementing
the last set bit of the current index, i.e., index = index + (index & (-index))
-
void update(int idx, int delta) { idx += 1; while (idx < bitArr.length) { this.bitArr[idx] += delta; idx = idx + (idx & -idx); } }
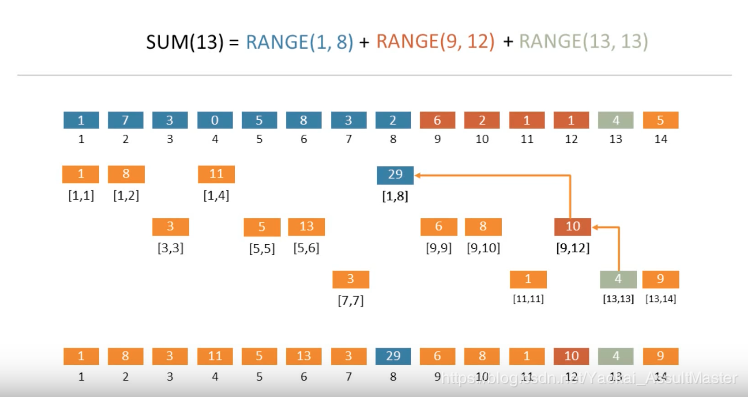
Visualization