Quick Union
1.Problem
Quick Union is a useful method to solve the dynamic connectivity problem, which can also be solved by depth-first search or breadth-first search.
2.Quick Union
-
Data structure
Integer array id[] of length N
id[i] is the parent of i, and to find the root of i, you are supposed to keep going until the parent doesn't change.
-
API
Connected(p,q) To judge whether p and q have the same root. Find(p) To find the root of p. Union(p,q) Set the id of p's root to the id of q's root. -
Code
int find(int p){ while(p!=id[p]){ p = id[p]; } return p; } bool connected(int p,int q){ return find(p)==find(q); } void Union(int p,int q){ int idp = find(p); int idq = find(q); if(connected(p,q)){ return; } id[idp] = idq; count --; }
3.Improvements
3.1 Weighting quick union
-
Idea
Balance by linking root of smaller tree to the root of lager tree
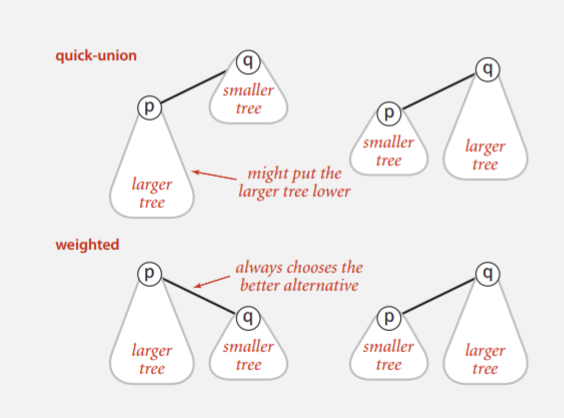
-
Data structure
Maintain extra array sz[] to count number of objects in the tree.
-
Code
void Union(int p,int q){ int idp = find(p); int idq = find(q); if(connected(p,q)){ return; } if(sz[idp]<sz[idq]){ id[idp] = idq; sz[idq] += sz[idp]; }else{ id[idq] = idp; sz[idp] += sz[idq]; } count --; } -
Summary
Through this improvement, run time can be reduced sharply from 2984ms to 52ms when the quick union is applied the 130th problem in the leetcode.
3.2 Path compression
-
Idea
When finding the node, just after computing the root of p, set the id[] of each examined node to point to that root.
-
Code
int find(int p){ int temp = p; while(p!=id[p]){ p = id[p]; } id[temp] = p; return p; }
3.3 Relationship between nodes
Quick Union only tells whether the two nodes belong to the same set, which in most case is enough to solve the problem. However, when there is a relative relationship between the nodes, another array should be introduced. For example, in POJ-1182, the food chain relationship between two nodes is needed. So, the data structure:
-
Data Structure
Maintain extra array relation[] to record the relationship between node p and its root.
In addition, the process of union and find should be adjusted. When compressing the path and connecting two nodes, the array relation[] may also change correspondingly. Specifically, the relationship transfer can be listed as follows:
-
(A,B),(B,C) ---> (A,C)
When finding the root of node p, we know the relationship between p and its current root id[p], as well as the relationship between id[p] and its root. We can then obtain the relationship between p and its root recursively.
-
(A,C),(B,C)->(A,B)
When querying the relationship between node p and node q, we can infer it through the relationship between p,q and their root.
-
(A,B),(A,C)->(B,C)
When connecting two trees, the relationships between node p and its root, node q and its root, p and q are known. And the relationship between node p's root and node q's root is needed. We can first find the relationship between p and the root of q through the relationship transfer (p,q),(q,q's root)->(p,q's root). And then (p's root, q's root) can be inferred through (p, p's root) and (p, q's root).






