😜查找😜

顺序查找

顺 序 查 找 法 的 特 点 ： 用 所 给 关 键 字 与 线 性 表 中 各 元 素 的 关 键 字' 逐 个 比 较 '， 直 到 成 功 或 失 败 。 存 储
结 构 通 常 为 顺 序 结 构 ， 也 可 为 链 式 结 构 。

typedef struct {
    ElemType *elem;
    int Len;    //表长
}Stable;

int Search(Stable St,ElemType key){
    St.elem[0] = key;   //哨兵
    //从后往前找
    for(i=St.Len; St.elem[i]!=key; --i)

    //若表中不存在关键字，则将查找到i=0时退出for循环
    return i;
}

折半查找

折半查找的思想：将表中间位置记录的关键字与查找 关 键 字 比 较 ， 如 果 两 者 相 等 ， 则 查 找 成 功 ； 否
则 利 用 中 间 位 置 记 录 将 表 分 成 前 、 后 两 个 子 表 ， 如 果 中 间 位 置 记 录 的 关 键 字 大 于 查 找 关 键 字 ， 则 进 一
步 查 找 前 一 子 表 ， 否 则 进 一 步 查 找 后 一 子 表 。 重 复 以 上 过 程 ， 直 到 找 到 满 足 条 件 的 记 录 ， 使 查 找 成 功 ，
或 直 到 子 表 不 存 在 为 止 ， 此 时 查 找 不 成 功 。

int BinarySer(SqList L,ElemType key){
    int low=0,hight=L.Len-1,mid;
    whlie(low <= hight){
        mid = (low+hight)/2;        //中间位置
        if(L.elem[mid] == key){
            return mid;
        }else if(L.elem[mid] > key){    //前半部分找
            hight = mid-1;
        }else{          //后半部分找
            low = mid-1;
        }
    }
    return -1;      //查找失败
}

查找成功与失败

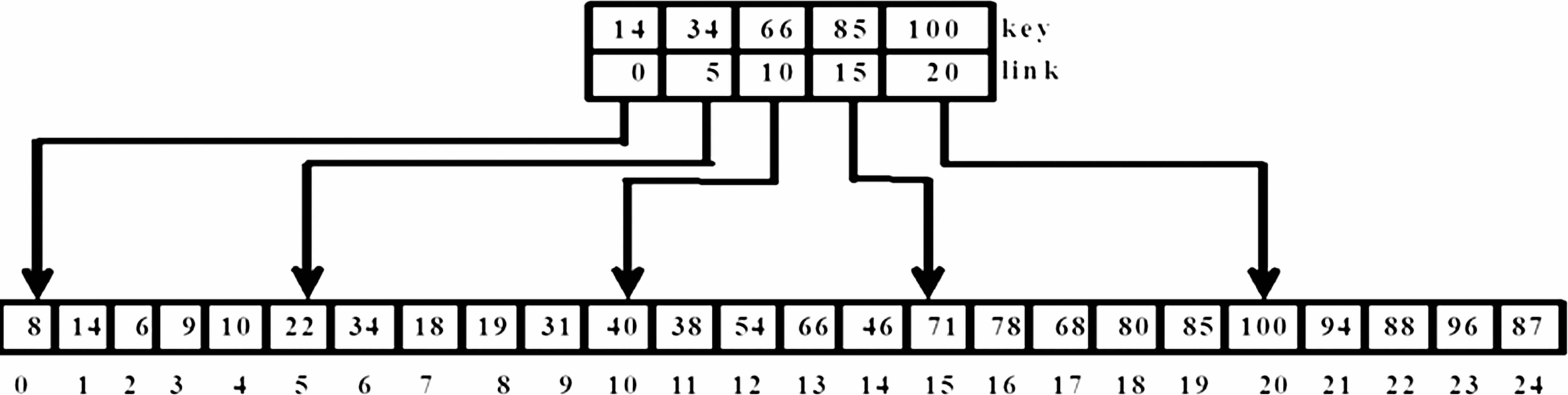
索引查找(分块查找)

基本思想：将查找表分为若干子块，块内的元素可以'无序',块之间是'有序'的
８， １４， ６， ９， １０， ２２， ３４， １８， １９， ３１，４０， ３８， ５４， ６６， ４６， ７１， ７８， ６８， ８０， ８５， １００， ９４， ８８， ９６， ８７
将25个记录分为5块，每块中有5个记录

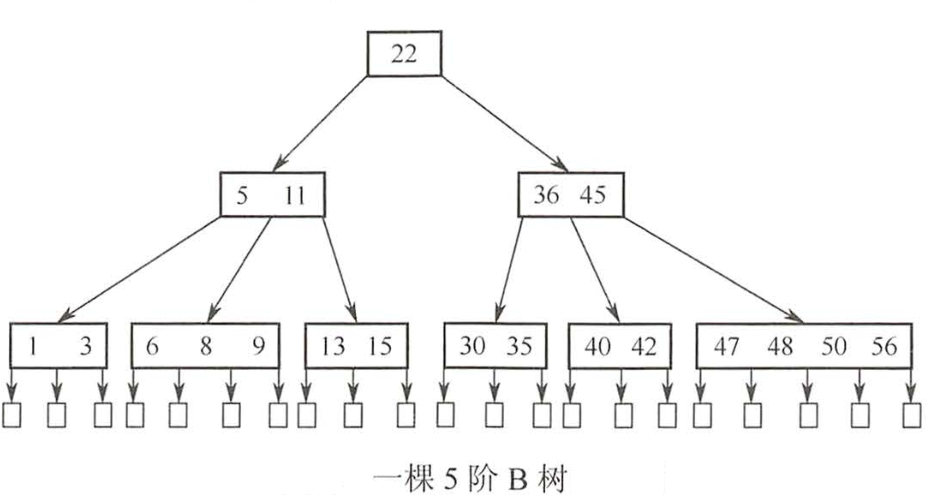
B树

B树是所有节点的'平衡因子'均等于0的多路平衡查找树
1.每个节点至多'有m棵子树'，至多含'有m-1个关键字'
2.若根不是终端节点，则'至少有两棵子树'
3.除根节点以外的所有'非叶子结点'至少有'⌈M/2⌉棵子树'，即至少含有'⌈M/2⌉(向上取整)-1个关键字'
4.※节点的'孩子个数'等于该节点中'关键字个数'加1
5.结点内各关键字互不相等且按从'小到大'排列
6.如果根节点有关键字，则其子树必然'大于等于'两棵，因为'子树个数等于关键字个数加1'

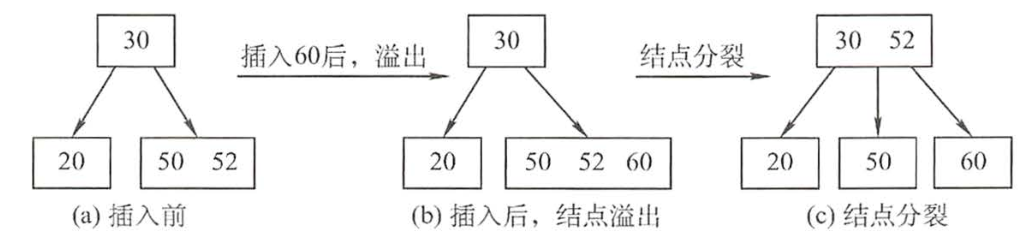
B树插入

插入后的节点关键字个数小于m可以'直接插'
当插入后的节点关键字个数'大于m-1'时，必须对节点进行'分裂'

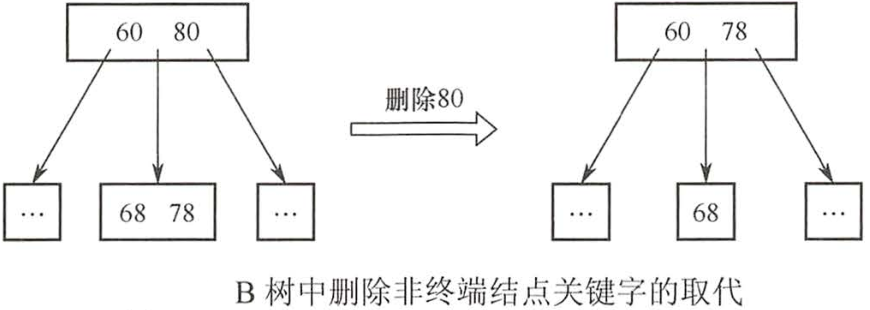
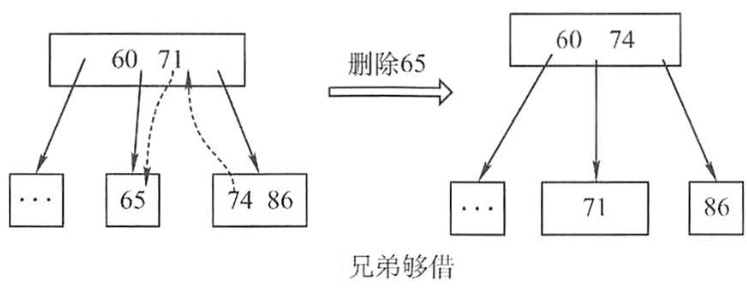
B树删除

1.被删除关键字所在的结点的关键字'个数大于⌈M/2⌉'，做删除操作不会破坏 B+树，则可以'直接删除'
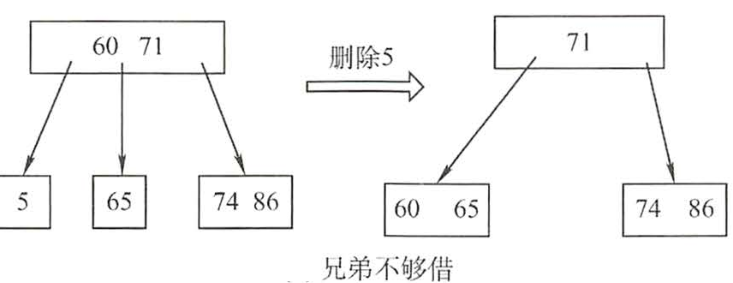
2.若被删除关键字所在节点删除前的关键字个数= ⌈M/2⌉，可以从'兄弟结点中借关键字'完成删除操作。
3.若兄弟'不够借'，则'兄弟和双亲节点合并'

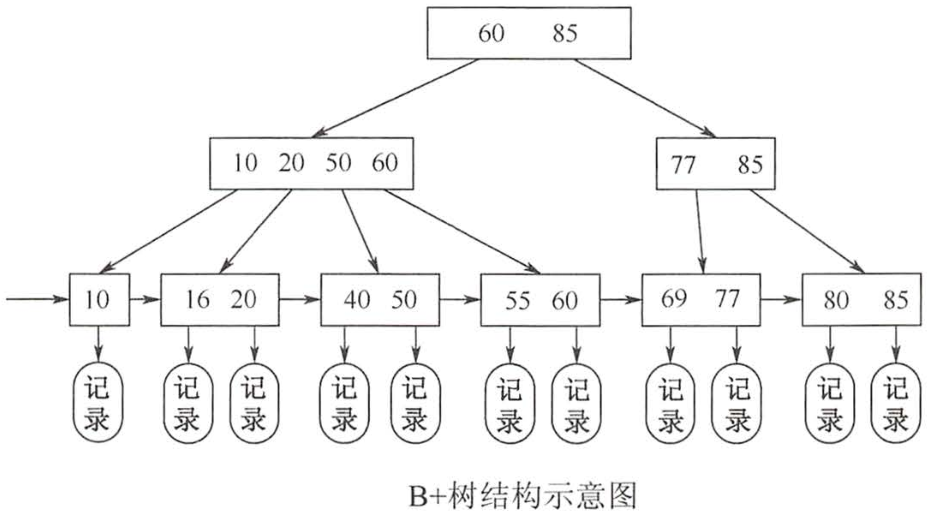
B+树

1.每个分支节点最多有'm棵子树'
2.非叶根节点至少有'两棵子树'，其他每个分支节点至少有⌈M/2⌉棵子树
3.节点的子树个数与关键字相等

B树与B+树的区别

1.B+：n个关键字的节点只含有'n'课树，B：n个关键字的节点含有'n+1'棵树
2.B+：每个节点关键字个数n的范围是'⌈M/2⌉≤n≤m'(根节点:1≤n≤m);B:每个节点关键字个数n的范围是'⌈M/2⌉-1≤n≤m-1'(根节点:1≤n≤m-1)

散列表

'散列表':它通过把关键码值映射到表中一个位置来访问记录，以加快查找的速度。这个映射函数叫做散列函数，存放记录的数组叫做散列表。

散列函数构造方法

1.'直接寻址法'：取关键字或关键字的某个线性函数值为散列地址。即H(key)=key或H(key) = a*key + b，其中a和b为常数（这种散列函数叫做自身函数）。
若其中H(key）中已经有值了，就往下一个找，直到H(key）中没有值了，就放进去。

2. '数字分析法'：分析一组数据，比如一组员工的出生年月日，这时我们发现出生年月日的前几位数字大体相同，这样的话，出现冲突的几率就会很大
，但是我们发现年月日的后几位表示月份和具体日期的数字差别很大，如果'用后面的数字来构成散列地址'，则冲突的几率会明显降低。因此数字分析法就是找出数字的规律，
尽可能利用这些数据来构造冲突几率较低的散列地址。

3. '平方取中法'：当无法确定关键字中哪几位分布较均匀时，可以先求出关键字的平方值，然后按需要'取平方值'的中间几位作为哈希地址。
这是因为：平方后中间几位和关键字中每一位都相关，故不同关键字会以较高的概率产生不同的哈希地址。 

4.'除留余数法'：取关键字被某个不大于散列表表长m的数p除后所得的余数为散列地址。即 'H(key) = key MOD p',p<=m。不仅可以对关键字直接取模，也可在折叠、
平方取中等运算之后取模。对p的选择很重要，'一般取素数或m'，若p选的不好，容易产生同义词。

冲突处理的方法

1. '开放寻址法'：'Hi=(H(key) + di) MOD m' ,i=1,2，…，k(k<=m-1），其中H(key）为散列函数，m为散列表长，di为增量序列，可有下列三种取法：
1.1. di=1,2,3，…，m-1，称线性探测再散列；
1.2. di=1^2,-1^2,2^2,-2^2，⑶^2，…，±（k)^2,(k<=m/2）称二次探测再散列；
1.3. di=伪随机数序列，称伪随机探测再散列。

2.'链地址法'：把所有的'同义词'存储在一个线性链表中

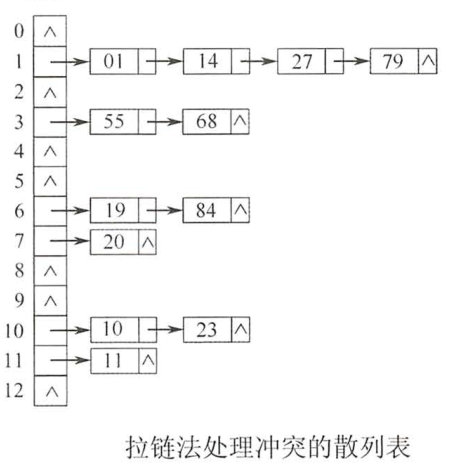
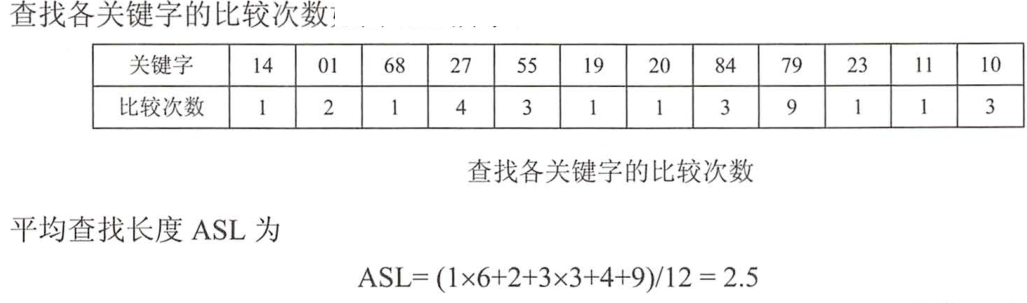
散列查找及性能分析

Tips:
1.散列表的装填因子定义为：'α= 填入表中的元素个数 / 散列表的长度'
2.，α'越大'，填入表中的元素较多，产生'冲突的可能性就越大'；α'越小'，填入表中的元素较少，'产生冲突的可能性就越小'。