森林与二叉树的应用
1.双亲表示法
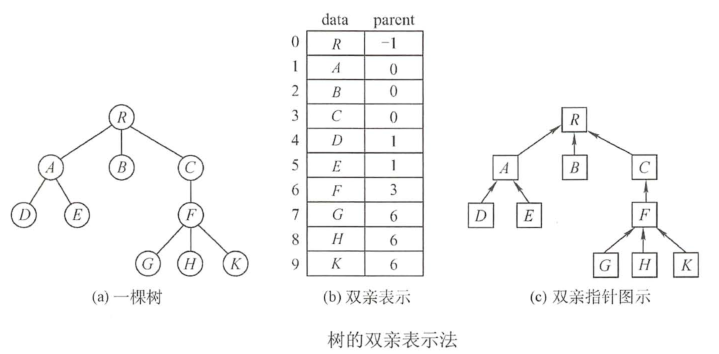
存储方式采用一组连续空间来存储每个节点，同时在每个节点上增设一个伪指针，
指示其双亲节点再数组中的位置，'根节点'下标为0，'伪指针'下标为1
该结构利用了每个几点只有唯一双亲的性质，可以很快得到每个节点的双亲节点，
但求节点的孩子时需要遍历整个结构。
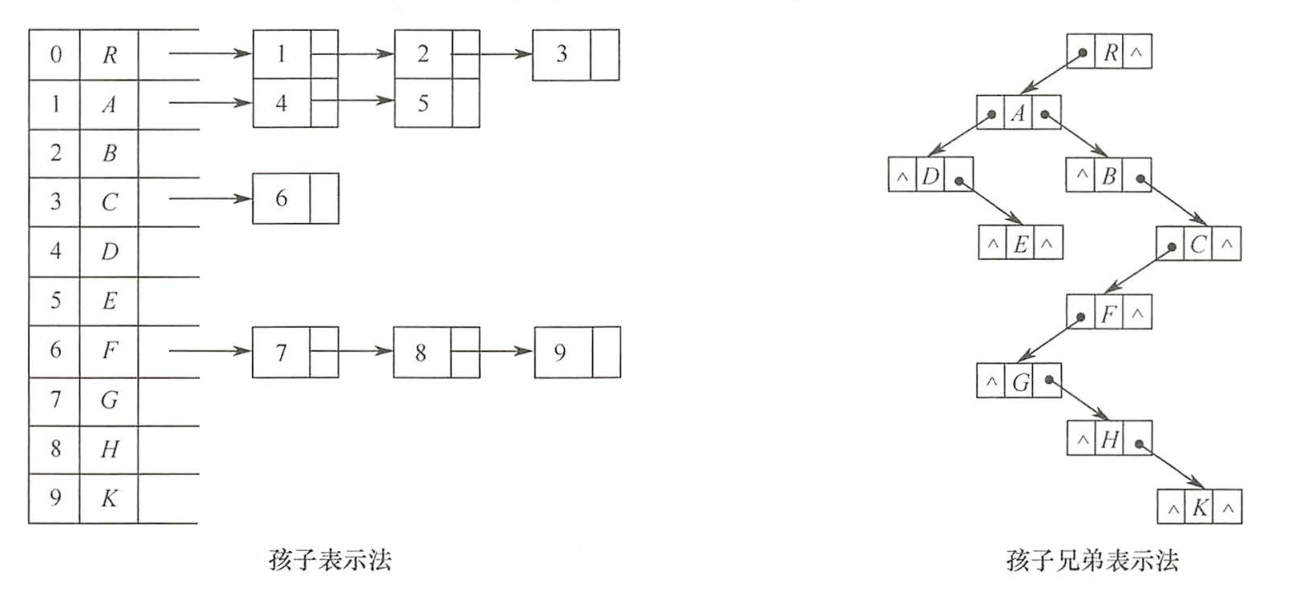
2.孩子兄弟表示法
最大的'优点'是可以方便的实现树转换二叉树，易于查找节点的孩子等，
'缺点'是从当前节点查找其双亲节点比较麻烦。
3.树、森林与二叉树的转换
①树-->二叉树
'左孩子右兄弟'：每个节点做指正指向她得第一个孩子，右节点指向它的书中的相邻的右兄弟
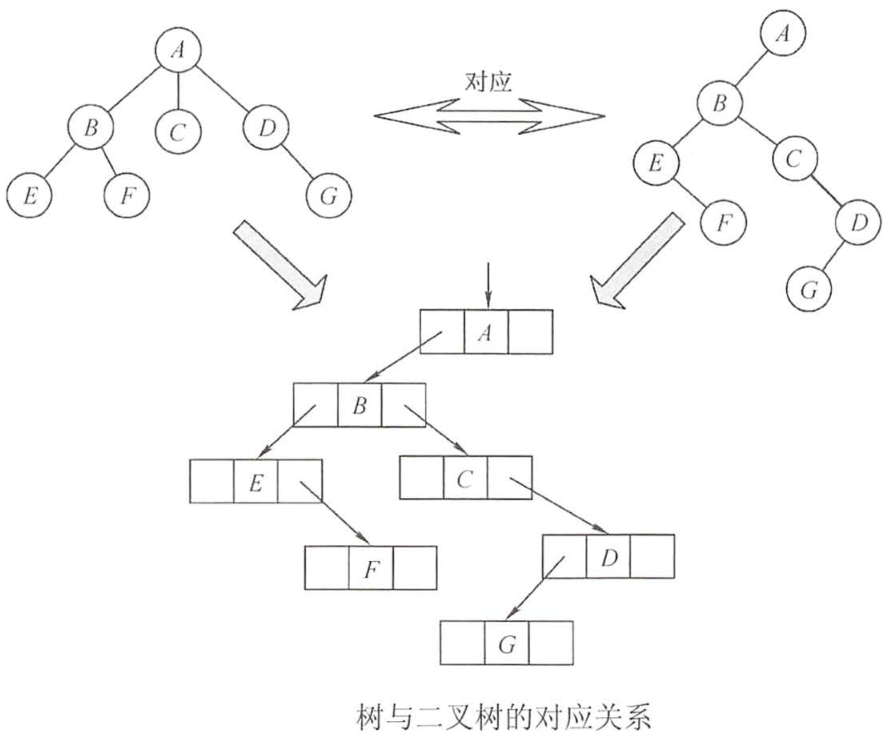
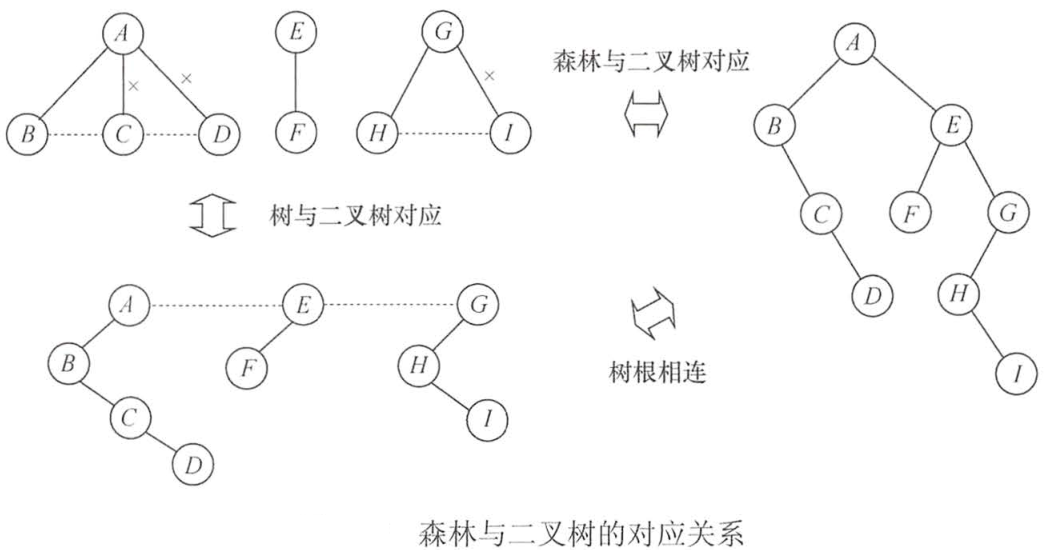
①森林-->二叉树
1.将森林的每棵树转换成相应的二叉树；2.每棵树的根也可视为兄弟关系
3.以第一棵树的根为轴心顺时针旋转45°
4.树的转换 相关习题
某二叉树先序为ABDEHCFIMGJKL，中序DBHEAIMFCGKLJ，画出这课二叉树，
并画出二叉树对应的森林
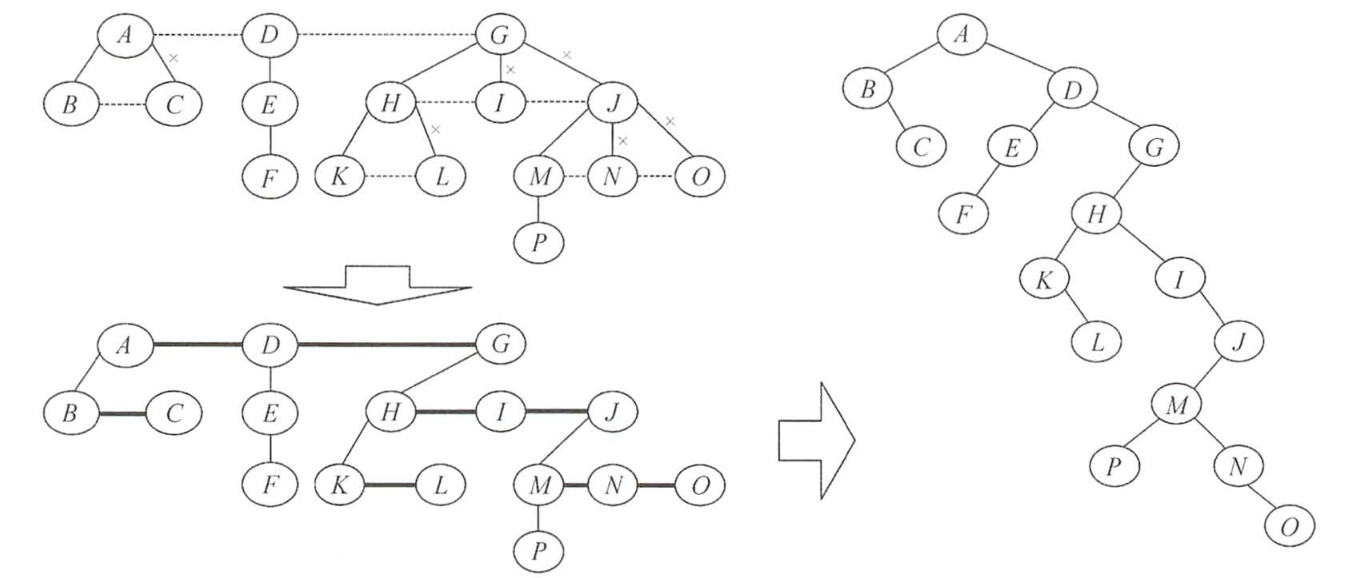
二叉树遍历的对应关系
| 树 | 森林 | 二叉树 |
|---|---|---|
| 先序 | 先序 | 先序 |
| 后序 | 中序 | 中序 |
5.二叉排序树
定义
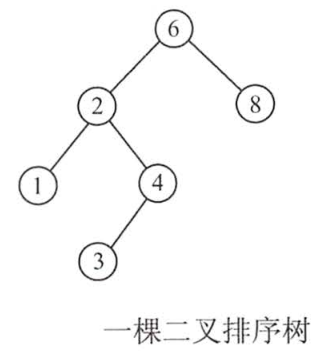
'左子树节点<根节点值<右子树节点'，对于二叉排序树进行中序遍历，可以得到一个'递增'序列,下图中序遍历序列为:'123468'
二叉排序树的删除
1)若删除节点z是叶节点，则直接删除
2)若z只有一颗左子树或右子树，则让z的子树代替z的位置(用子女代替)
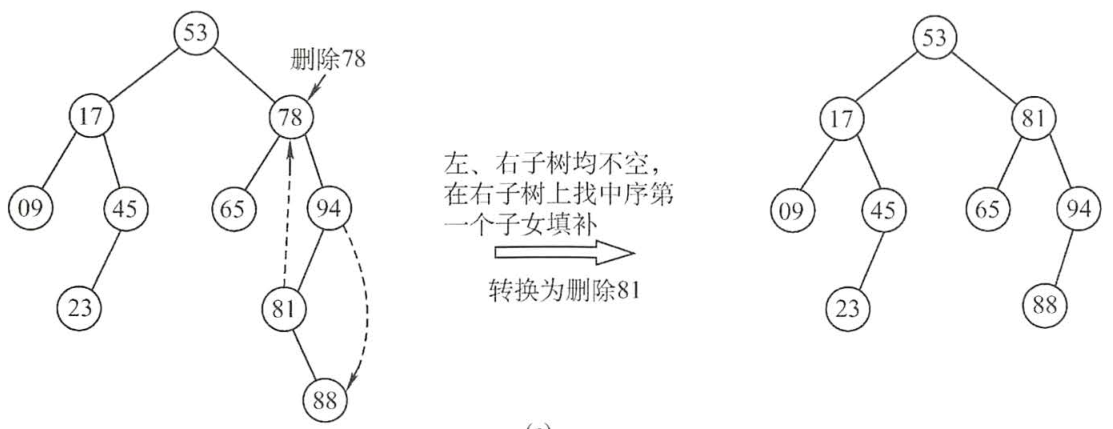
3)若z有左右子树，找第一个子女来填补
2图
3图
二叉排序树的平均查找效率
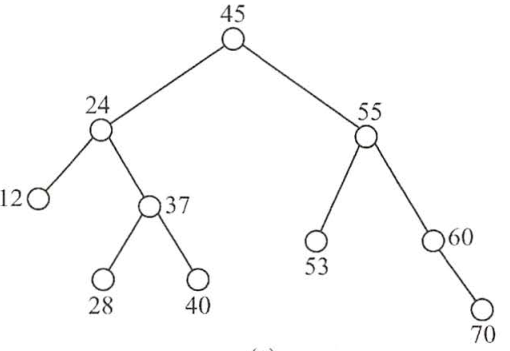
上图的查找效率为 'ASL=(1+2*2+3*4+4*3)/10=2.9' 即'每层节点总数乘以所在层数求和取平均'
6.平衡二叉树
任意节点的'左右子树高度差的绝对值不超过1'，这样的二叉树称为'平衡二叉树';
左右子树的高度差称为节点的'平衡因子'
-->平衡 如下
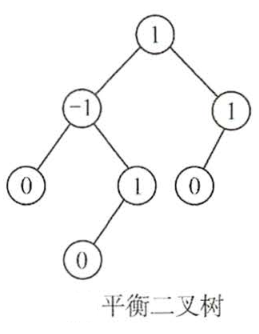
-->不平衡 如下
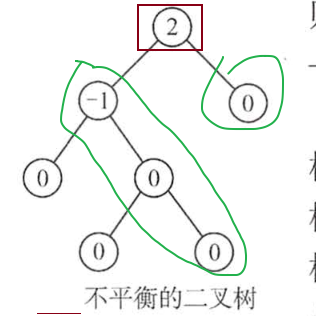
※平衡二叉树的插入
下图为'RR右单旋转'
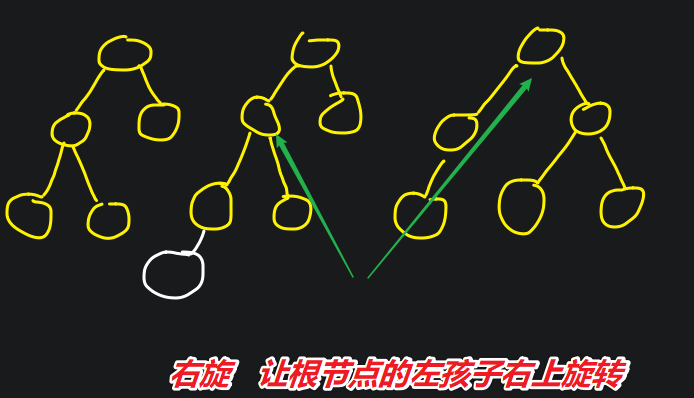
下图为'LL左单旋转'
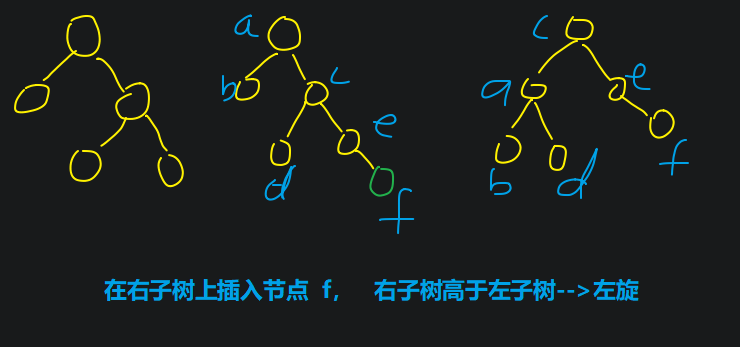
下图为 'LR先左后右 旋转'
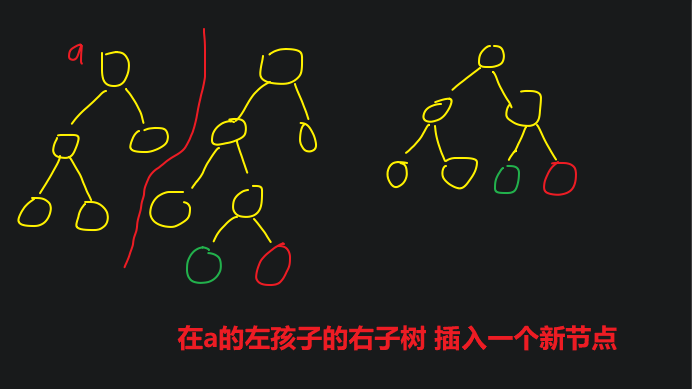
下图为 'RL先右后左 旋转'
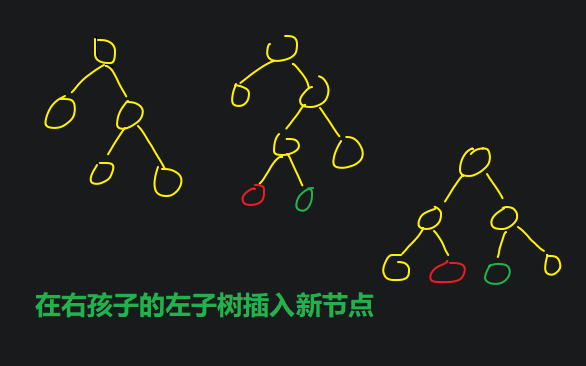
7.哈夫曼树
树中节点常常被赋予一个表示某种意义的数值称为'权';
树中所有叶节点的带权路径长度之和称为该树的'带权路径长度-->WPL'
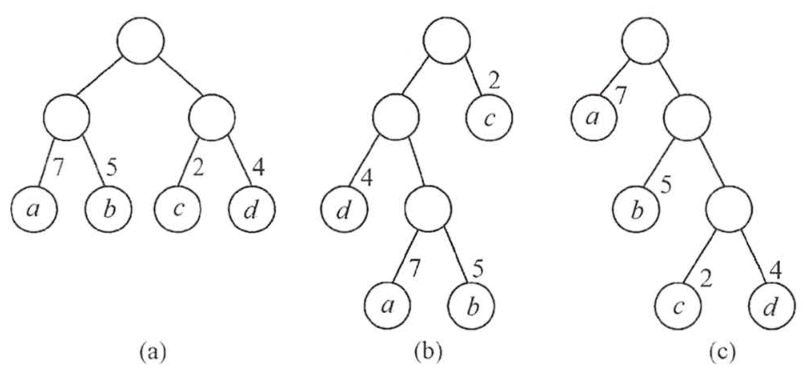
下图带权路径计算
(a) WPL=7×2+5×2+2×2+4×2=36
(b) WPL = 7×3+5×3+4×2+1×2=46
(c)WPL=7×1+5×2+2×3+4×3=35
哈夫曼树的构造
1--森林中选择出两颗结点的'权值最小'的二叉树
2--合并两颗二叉树，增加一个新的节点作为'新的二叉树的根'，权值为'左右孩子的权值之和'
哈夫曼编码
若没有一个编码是另一个编码的'前缀',则称这样的编码为'前缀编码'
由于时间有限，写的不好请见谅，理解万岁(:
以上图片均来自
王道数据结构书中仅为个人复习方便所写，如有侵权立即删除！
由于时间有限，写的不好请见谅，理解万岁(:
