动态规划-背包问题

01背包

题意

 

 

 算法思路

 

 

 

#include<bits/stdc++.h>

using namespace std;

const int MAXN = 1005;
int v[MAXN];    // 体积
int w[MAXN];    // 价值 
int f[MAXN][MAXN];  // f[i][j], j体积下前i个物品的最大价值 

int main() 
{
    int n, m;   
    cin >> n >> m;
    for(int i = 1; i <= n; i++) 
        cin >> v[i] >> w[i];

    for(int i = 1; i <= n; i++) 
        for(int j = 1; j <= m; j++)
        {
            //  当前背包容量装不进第i个物品，则价值等于前i-1个物品
            if(j < v[i]) 
                f[i][j] = f[i - 1][j];
            // 能装，需进行决策是否选择第i个物品
            else    
                f[i][j] = max(f[i - 1][j], f[i - 1][j - v[i]] + w[i]);
        }           

    cout << f[n][m] << endl;

    return 0;
}

 

 

#include<bits/stdc++.h>
using namespace std;
const int maxn=1e3+10;
int N,V;
int v[maxn],w[maxn];
int dp[maxn];
int main()
{
    int i,j;
    cin>>N>>V;
    for(i=1;i<=N;i++)
        cin>>v[i]>>w[i];
    for(i=1;i<=N;i++)
    {
        for(j=V;j>=v[i];j--)
            dp[j]=max(dp[j],dp[j-v[i]]+w[i]);
    }
    cout<<dp[V]<<endl;
    return 0;
}

完全背包

题意

 

 

算法思路

 

 

#include<bits/stdc++.h>
using namespace std;
const int maxn=1010;
int N,V;
int v[maxn],w[maxn];
int dp[maxn];

int main()
{
    int i,j;
    cin>>N>>V;
    for(i=0;i<N;i++)
        cin>>v[i]>>w[i];
    for(i=0;i<N;i++)
    {
        for(j=v[i];j<=V;j++)
            dp[j]=max(dp[j],dp[j-v[i]]+w[i]);
    }
    cout<<dp[V];
    return 0;
}

多重背包

题意

 

 算法思路

#include<bits/stdc++.h>
using namespace std;
const int maxn=1e3+10;
int N,V;
int w[maxn],v[maxn],s[maxn];
int dp[maxn][maxn];
int main()
{
    int i,j,k;
    cin>>N>>V;
    for(i=1;i<=N;i++)
        cin>>v[i]>>w[i]>>s[i];
    for(i=1;i<=N;i++)
    {
        for(j=0;j<=V;j++)
        {
            for(k=0;k<=s[i]&&k*v[i]<=j;k++)
                dp[i][j]=max(dp[i][j],dp[i-1][j-k*v[i]]+k*w[i]);
        }
    }
    cout<<dp[N][V]<<endl;
    return 0;
}

若是数据范围有所调整

 

 

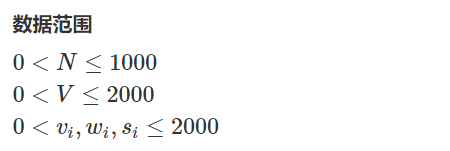
则该方法不可使用，可使用01背包+二进制优化的方法

 

 

#include<bits/stdc++.h>
using namespace std;
const int n=12010,m=2010;
int N,V;
int v[n],w[n];
int f[m];

int main()
{
    int i,j;
    cin>>N>>V;
    int cnt=0;
    for(i=0;i<N;i++)
    {
        int a,b,c;
        cin>>a>>b>>c;

        int k=1;
        while(k<=c)
        {
           cnt++;
           v[cnt]=a*k;
           w[cnt]=b*k;
           c-=k;
           k*=2;
        }
        if(c>0)
        {
            cnt++;
            v[cnt]=a*c;
            w[cnt]=b*c;
        }
    }
    N=cnt;
    for(i=1;i<=N;i++)
    {
        for(j=V;j>=v[i];j--)
            f[j]=max(f[j],f[j-v[i]]+w[i]);
    }
    cout<<f[V]<<endl;
    return 0;
}

分组背包

题意

 

 

算法思路

 

 

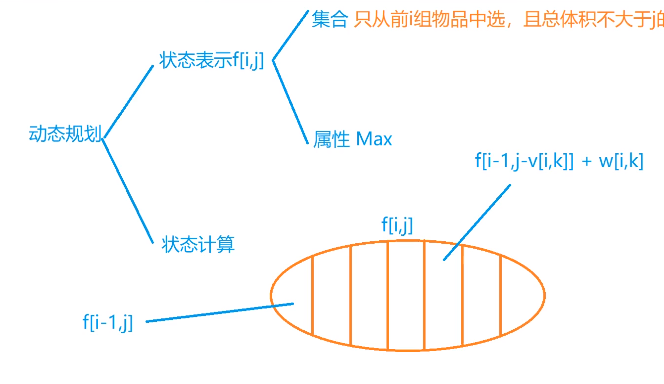
#include<bits/stdc++.h>
using namespace std;
int s[110];
int v[110][110],w[110][110];
int f[110];

int main()
{
    int i,j,k;
    int N,V;
    cin>>N>>V;
    for(i=0;i<N;i++)
    {
        cin>>s[i];
        for(j=0;j<s[i];j++)
            cin>>v[i][j]>>w[i][j];
    }
    for(i=0;i<N;i++)
    {
        for(j=V;j>=0;j--)
        {
            for(k=0;k<s[i];k++)
            {
                if(j>=v[i][k])
                    f[j]=max(f[j],f[j-v[i][k]]+w[i][k]);
            }
        }
    }
    cout<<f[V]<<endl;
    return 0;
}