最短路-SPFA算法&Floyd算法

SPFA算法

算法复杂度

SPFA 算法是 Bellman-Ford算法 的队列优化算法的别称，通常用于求含负权边的单源最短路径，以及判负权环。

SPFA一般情况复杂度是O(m)最坏情况下复杂度和朴素 Bellman-Ford 相同，为O(nm)。

n为点数，m为边数

spfa也能解决权值为正的图的最短距离问题，且一般情况下比Dijkstra算法还好

算法步骤

queue <– 1
while queue 不为空
 (1) t <– 队头
 queue.pop()
 (2)用 t 更新所有出边 t –> b，权值为w
 queue <– b (若该点被更新过，则拿该点更新其他点)

代码实现

题目：https://www.acwing.com/problem/content/description/853/

#include<bits/stdc++.h>
using namespace std;
const int maxn=2e5+10;
typedef long long ll;
ll n,m;
typedef pair<int, int> PII;
int h[maxn],e[maxn],w[maxn],ne[maxn],idx;
int dist[maxn];
bool st[maxn];

void add(int x,int y,int c)
{
    //权值记录
    w[idx]=c;
    //终点边记录
    e[idx]=y;
    //存储编号为idx的边的前一条边的编号
    ne[idx]=h[x];
    //代表以x为起点的边的编号，这个值会发生变化
    h[x]=idx++;
}


ll spfa()
{
    ll i,j;
    memset(dist,0x3f,sizeof(dist));
    dist[1]=0;

    queue<int> q;
    //将起点加入
    q.push(1);
    //标记已在集合
    st[1]=true;
    while(q.size())
    {
        int t=q.front();
        q.pop();
        //弹出后，不在集合
        st[t]=false;
        for(i=h[t];i!=-1;i=ne[i])
        {
            //获得终点
            j=e[i];
            //判断距离
            if(dist[j]>dist[t]+w[i])
            {
                //更新距离
                dist[j]=dist[t]+w[i];
                //判断终点是否在集合
                if(!st[j])
                {
                    //加到集合，继续更新他到其他点的最短距离
                    q.push(j);
                    st[j]=true;
                }
            }
        }
    }
    //如果说原点到终点n的距离还是无穷，则代表到达不了
    if(dist[n]==0x3f3f3f3f)
        return -1;
    else
        return dist[n];
}

int main()
{
    ll i,j;
    cin>>n>>m;
    //初始化h数组为-1，目的是为ne数组赋值
    memset(h,-1,sizeof(h));
    while(m--)
    {
        int x,y,z;
        cin>>x>>y>>z;
        //加边
        add(x,y,z);
    }
    ll ans=spfa();
    if(ans==-1)
        cout<<"impossible";
    else
        cout<<ans;
    return 0;
}

SPFA判断负环

求负环方法

统计当前每个点的最短路中所包含的边数，如果某点的最短路所包含的边数大于等于n，则也说明存在环。

算法步骤

①初始化要将所有点都插入到队列中

②增加一个cnt数组，来记录走的边个数

③若dist[j] > dist[t] + w[i],则表示从t点走到j点能够让权值变少，因此进行对该点j进行更新，并且对应cnt[j] = cnt[t] + 1,往前走一步

注意：该题是判断是否存在负环，并非判断是否存在从1开始的负环，因此需要将所有的点都加入队列中，更新周围的点

代码实现

题目：https://www.acwing.com/problem/content/description/854/

#include<bits/stdc++.h>
using namespace std;
const int maxn=2e5+10;
typedef long long ll;
ll n,m;
typedef pair<int, int> PII;
int h[maxn],e[maxn],w[maxn],ne[maxn],idx;
int dist[maxn],cnt[maxn];
bool st[maxn];

void add(int x,int y,int c)
{
    //权值记录
    w[idx]=c;
    //终点边记录
    e[idx]=y;
    //存储编号为idx的边的前一条边的编号
    ne[idx]=h[x];
    //代表以x为起点的边的编号，这个值会发生变化
    h[x]=idx++;
}


bool spfa()
{
    ll i,j;
    queue<int> q;
    //将所有点加入队列
    for(i=1;i<=n;i++)
    {
        q.push(i);
        st[i]=true;
    }
    while(q.size())
    {
        int t=q.front();
        q.pop();
        st[t]=false;
        for(i=h[t];i!=-1;i=ne[i])
        {
            j=e[i];
            //dist数组不用初始化，是因为如果为负的就进行更新，才能找出负环
            if(dist[j]>dist[t]+w[i])
            {
                dist[j]=dist[t]+w[i];
                //边数更新
                cnt[j]=cnt[t]+1;
                //大于n-1条边，代表有负环
                if(cnt[j]>=n)
                    return true;
                if(!st[j])
                {
                    q.push(j);
                    st[j]=true;
                }
            }
        }
    }
    return false;
}

int main()
{
    ll i,j;
    cin>>n>>m;
    //初始化h数组为-1，目的是为ne数组赋值
    memset(h,-1,sizeof(h));
    while(m--)
    {
        int x,y,z;
        cin>>x>>y>>z;
        //加边
        add(x,y,z);
    }
    //堆优化版的Dijkstra

    if(spfa())
        cout<<"Yes";
    else
        cout<<"No";
    return 0;
}

Floyd算法

原理

多源汇最短路问题

算法步骤

①初始化d
②k, i, j 去更新d

代码实现

题目：https://www.acwing.com/problem/content/description/856/

#include<bits/stdc++.h>
using namespace std;
int n,m,k;
const int maxn=220,INF=0x3f3f3f3f;
int d[maxn][maxn];

void floyd()
{

    for(int k=1;k<=n;k++)
    {
        for(int i=1;i<=n;i++)
        {
            for(int j=1;j<=n;j++)
                d[i][j]=min(d[i][j],d[i][k]+d[k][j]);
        }
    }

}

int main()
{
    int i,j;
    cin>>n>>m>>k;
    for(i=1;i<=n;i++)
    {
        for(j=1;j<=n;j++)
        {
            if(i==j)
                d[i][j]=0;
            else
                d[i][j]=INF;
        }
    }

    while(m--)
    {
        int x,y,z;
        cin>>x>>y>>z;
        d[x][y]=min(d[x][y],z);
    }
    floyd();

    while(k--)
    {
        int x,y;
        cin>>x>>y;
        if(d[x][y]>INF/2)
            cout<<"impossible"<<endl;
        else
            cout<<d[x][y]<<endl;
    }

    return 0;
}

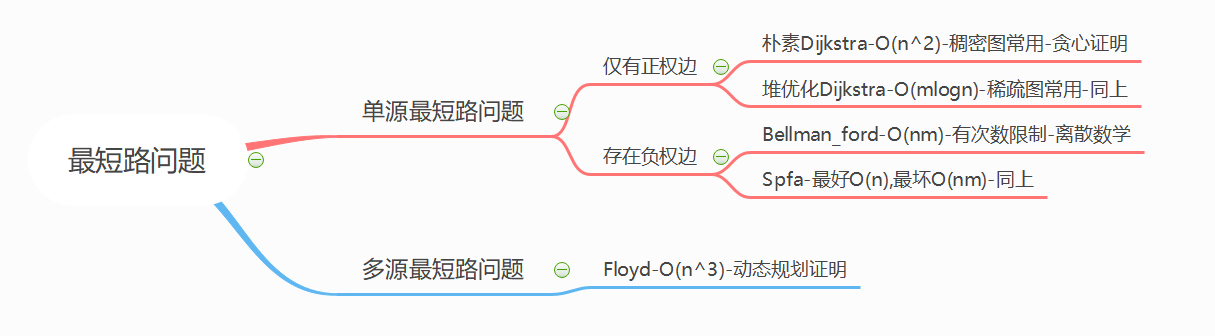
最短路总结