暑假集训感悟
这个暑假并没有愉快的回家,吹着空调吃着西瓜,抱着电脑打着游戏,而是选择了留在学校,继续我的ACM学习之旅!!!
训练了11天,感觉自己还是有很多没有学习的透彻,只是简单的了解啦一下,做了几道入门题(比如说:树状数组和线段树)
上题吧!!
树状数组入门1
https://www.luogu.org/problemnew/show/P3374
树状数组的表示形式
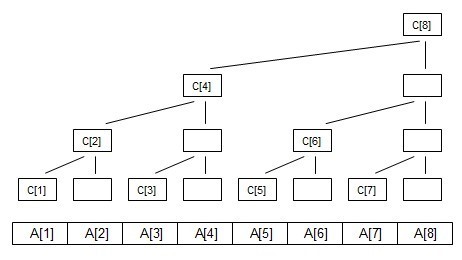
这是一道简单的入门题,题意大概是:对一个数列有两种操作
1.将某一个数加上x
2.求某区间的和
利用树状数组的三个基本函数
①
long long lowbit(long long x) { return x&(-x); }
②添加某个数
void add(long long i,long long x) { while(i<=n) { c[i]+=x; i+=lowbit(i); } }
③求前几项的和
long long sum(long long x) { long long ans=0; while(x>0) { ans+=c[x]; x-=lowbit(x); } return ans; }
代码:
#include<iostream> using namespace std; long long c[500005],a[500005],n; long long lowbit(long long x) { return x&(-x); } void add(long long i,long long x) { while(i<=n) { c[i]+=x; i+=lowbit(i); } } long long sum(long long x) { long long ans=0; while(x>0) { ans+=c[x]; x-=lowbit(x); } return ans; } int main() { long long m,i,j,k,e,d,t; cin>>n>>m; for(i=1;i<=n;i++) { cin>>a[i]; add(i,a[i]); } while(m--) { cin>>t>>e>>d; if(t==1) { add(e,d); } if(t==2) { cout<<sum(d)-sum(e-1)<<endl; } } return 0; }
AC了
接下来说个线段树的案例
线段树1
https://www.luogu.org/problemnew/show/P3372
题意为:
已知一个数列,你需要进行下面两种操作:
1.将某区间每一个数加上x
2.求出某区间的和
线段树操作有三步
构建线段树
add增加区间里的每一个数
求区间数的和
#include<iostream> using namespace std; struct nod { long long l,r,root,lazy,sum; }t[800005]; long long a[800005]; void buildtree(long long l,long long r,long long root) { t[root].l=l;t[root].r=r; long long x=(t[root].l+t[root].r)/2,ch=root*2; if(t[root].l==t[root].r) { t[root].sum=a[l]; return ; } buildtree(l,x,ch); buildtree(x+1,r,ch+1); t[root].sum=t[ch].sum+t[ch+1].sum; } void add(long long l,long long r,long long root,long long num) { long long x=(t[root].l+t[root].r)/2,ch=root*2; if(t[root].l==l&&t[root].r==r) { t[root].lazy+=num; return ; } if(r<=x) add(l,r,ch,num); if(l>x) add(l,r,ch+1,num); if(l<=x&&r>x) { add(l,x,ch,num); add(x+1,r,ch+1,num); } t[root].sum+=(r-l+1)*num; } long long finds(long long l,long long r,long long root) { if(l>r) return 0; long long x=(t[root].l+t[root].r)/2,ch=root*2; if(t[root].lazy) { t[root].sum+=(t[root].r-t[root].l+1)*t[root].lazy; if(t[root].l!=t[root].r) { t[ch].lazy+=t[root].lazy; t[ch+1].lazy+=t[root].lazy; } t[root].lazy=0; } if(t[root].l==l&&t[root].r==r) return t[root].sum; if(r<=x) return finds(l,r,ch); if(l>x) return finds(l,r,ch+1); if(l<=x&&r>x) { return finds(l,x,ch)+finds(x+1,r,ch+1); } } int main() { long long n,c,d,p,q,i,k; cin>>n; for(i=1;i<=n;i++) cin>>a[i]; buildtree(1,n,1); cin>>q; while(q--) { cin>>k; if(k==1) { cin>>c>>d>>p; add(c,d,1,p); } if(k==2) { cin>>d; cout<<finds(1,d,1)-finds(1,d-1,1)<<endl; } } return 0; }
AC了
学习了一些图论的基本知识:用数组来存图,用邻接表来存图和用链式前向星的方法存图。
详情可以看看学长的博客:https://blog.csdn.net/yhl1999/article/details/89320467
来看一下如何用矩阵来存图:
int MAX_V=4; //节点个数 bool G[MAX_V+1][MAX_V+1]; //矩阵的声明 void add_edge(int u,int v) //添加一条以u为起点,v为终点的边 { G[u][v] = true; //G[u][v]=true 代表以点u为起点,点v为终点有一条边 } int main() { add_edge(1,2); add_edge(2,3); add_edge(4,3); add_edge(4,2); }
2.利用邻接表来存储图
使用邻接表来存图可以有效的解决点数过多的问题。对于图中任意一个顶点来说,邻接表将以该点为起点的所有的边以链表的形式连接起来,“挂”在顶点下面,可以有效的节省空间。
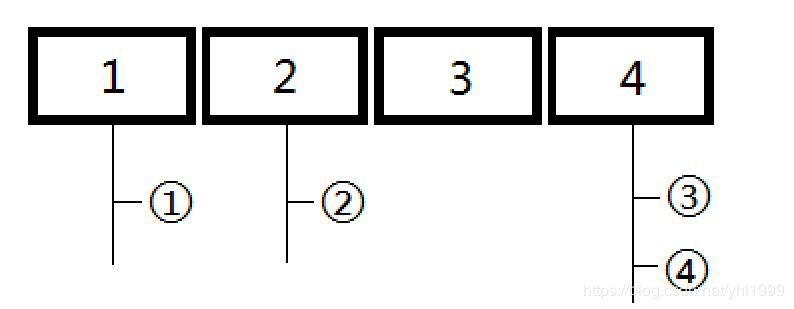
图中带圈的数字代表边的序号。
邻接表的实现又可以分为用vector实现与用链式前向星实现
利用vector建立临接表实现图的存储
#include<vector> int MAX_E = 4; //边数 int MAX_V = 4; //节点数 struct edge{ //建立边的结构体 int v,w; //v-边的终点,w-边的权值,由于边直接挂在起点下所以不许要存储起点的序号 }; vector<edge> G[MAX_V+1]; //由vector数组建立邻接表存图 G[i]代表编号为i的点的边集 void add_edge(int u,int v,int w){ edge e; e.v=v; e.w=w; G[u].push_back(e); /*熟练可以直接写成 G[u].push_back(edge{v,w}); */ } int main() { add_edge(1,2,1); add_edge(2,3,1); add_edge(4,3,1); add_edge(4,2,1); }
链式前向星存储无向图
#include<bits/stdc++.h> using namespace std; const int maxn = 1005;//点数最大值 int n, m, cnt;//n个点,m条边 struct Edge { int v, w, next;//终点,边权,同起点的上一条边的编号 }edge[maxn];//边集 int head[maxn];//head[i],表示以i为起点的第一条边在边集数组的位置(编号) void init()//初始化 { for (int i = 0; i <= n; i++) head[i] = -1; cnt = 0; } void add_edge(int u, int v, int w)//加边,u起点,v终点,w边权 { edge[cnt].v = v; //终点 edge[cnt].w = w; //权值 edge[cnt].next = head[u];//以u为起点上一条边的编号,也就是与这个边起点相同的上一条边的编号 head[u] = cnt++;//更新以u为起点上一条边的编号 } int main() { cin >> n >> m; int u, v, w; init();//初始化 for (int i = 1; i <= m; i++)//输入m条边 { cin >> u >> v >> w; //add_edge(u, v, w);//加边 //加双向边 add_edge(u, v, w); add_edge(v, u, w); } for (int i = 1; i <= n; i++)//n个起点 { cout << i << endl; for (int j = head[i]; j != -1; j = edge[j].next)//遍历以i为起点的边 { cout << i << " " << edge[j].v << " " << edge[j].w << endl; } cout << endl; } return 0; }
跟着学长一起打比赛,一起听直播讲题,确实是件很享受的事情,特别是听大佬讲题,更是觉得自己就是个菜鸡,若到爆了。
最近一直在补提,上回博客分享的是2019河北省省赛的题,之后还会给大家分享一些有价值的题。
未来可期,充分利用时间==MAX(value(人生无限的财富))


 浙公网安备 33010602011771号
浙公网安备 33010602011771号