B树和B+树
简介
B树和B+树都是多路查找树，为了解决数据量大，树的高度大增(二叉树)而产生的一种数据结构，23树和234树都是一种特殊的B树，为了更好理解B树，故先介绍23树和234树。
23树
定义
2-3树是一种多路查找树，2和3的意思是该树包含2结点和3结点两种情况；
- 2结点包含一个元素和两个子树
- 左子树包含结点的元素值小于该结点的元素值，右子树包含结点的元素值大于该结点的元素值
- 2结点要不有两个子树，要不就没有子树，不允许只有一个子树。
- 3结点包含一大一小两个元素和三个子树，元素按照左小右大顺序排列；
- 左子树包含结点的元素值小于该结点较小的元素值，右子树包含结点的元素值大于该结点较大的元素值，中间子树包含的结点的元素值介于这两个元素值之间。
- 3结点要不有三个子树，要不就没有子树，不允许有一个或者两个子树。
- 2-3树所有叶子结点都在同一层次
- 图例
234树
定义
2-3-4树是一种多路查找树，2和3和4的意思是该树包含2结点、3结点和4结点三种情况；
2-3树是一种多路查找树，2和3的意思是该树包含2结点和3结点两种情况；
- 2结点包含一个元素和两个子树
- 左子树包含结点的元素值小于该结点的元素值，右子树包含结点的元素值大于该结点的元素值
- 2结点要不有两个子树，要不就没有子树，不允许只有一个子树。
- 3结点包含一大一小两个元素和三个子树，元素按照左小右大顺序排列；
- 左子树包含结点的元素值小于该结点较小的元素值，右子树包含结点的元素值大于该结点较大的元素值，中间子树包含的结点的元素值介于这两个元素值之间。
- 3结点要不有三个子树，要不就没有子树，不允许有一个或者两个子树。
- 4结点包含小中大三个元素和四个子树。
- 最左子树包含的结点的元素值小于该结点最小的元素值，第二个子树包含的结点的元素值大于最小的元素值小于中间元素值，第三个子树包含的的结点的元素值大于中间元素值小于最大元素值，最右子树包含的结点的元素值大于该结点最大的元素值。
- 4结点要不有四个子树，要不就没有子树，不允许有一个、两个子树或三个子树。
- 2-3-4树所有叶子结点都在同一层次
- 图例
略，和2-3树基本一致，区别就是多了一个4结点。
B树
定义
B树也是一种平衡的多路查找树，2-3树和2-3-4树都是B树的特例，我们把树中结点最大的子树数目称为B树的阶。通常记为m。
一颗m阶B树或为空树，或为满足如下特性的m叉树：
- 树中每个结点至多有m棵子树。(即至多含有m-1个关键字，两颗子树指针夹着一个关键字)；
- 若根结点不是终端结点，则至少有两颗子树。(至少一个关键字)；
- 除根结点外的所有非叶子结点至少有[m/2]棵子树。(即至少含有[m/2]-1个关键字)；
- 所有的叶子结点出现在同一个层次上，不带信息。(就像是折半查找判断树中查找失败的结点)。
- 每一个结点中的关键字满足从左到右依次增大的规则。
B树的查找操作
B树是多路查找树，二叉排序树是二路查找，B树是多路查找，所以它是二叉排序树的拓展。因此，B树的查找操作和二叉排序树的查找操作非常类似。
查找过程：
① 先让待查找关键字key和结点中的关键字比较，如果等于某个关键字，则查找成功。
② 如果和所有的关键字都不相等，则看key处在哪个范围内，然后去对应的指针所指向的子树中查找。
例: 如果Key比第一个关键字K1还小，则去P0指针所指向的子树中查找，如果比最后一个关键字KN还大，则去PN指针所指向的子树中查找。
- 查找案例
如图3阶B树， 查找11key值。
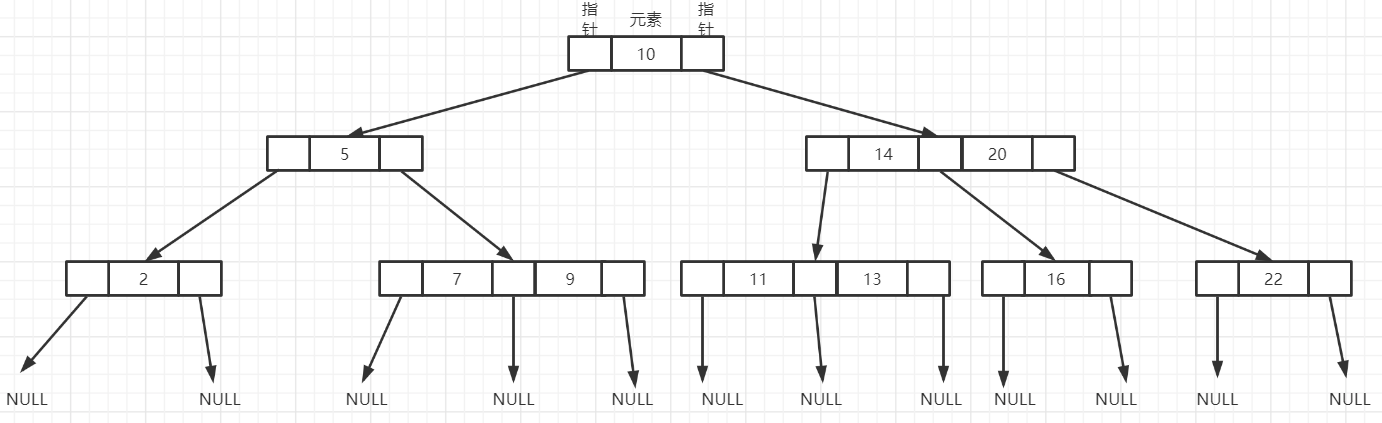
第一步：和跟节点10比较，不等且比10大，去右边的子树中查找；
第二步: 和右子树中关键字14比较，不等且比14小，故去左子树中查找；
第三步：和左子树中关键字11比较，相等，获取其data，返回。
B树的插入操作
在二叉排序树中，仅需查找到需插入的终端结点的位置。但是，在B树中找到插入的位置后，并不能简单地将其添加到终端结点位置，因为此时可能会导致整棵树不再满足B树中定义中的要求。
- 例如:
给定一组关键字{20,30,50,52,60,68,70}，创建一颗3阶B树的过程。
- 分析：非叶子结点至少有[m/2]-1个关键字,即1个关键字；至多含有m-1个关键字，即2个关键字
第一步:取两个key作为根结点。
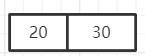
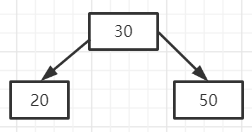
第二步:再取一个key50插入，如下图，但是每个结点最多有两个关键字，所有这个结点不能满足B树的要求，需要分裂。
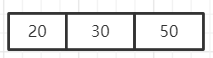
分裂的方法:取这个关键字数组中的中间关键字([n/2])作为新的结点，然后其他关键字形成两个结点作为新结点的左右子结点。
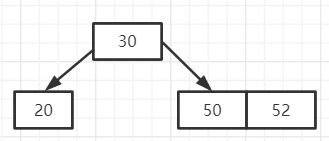
第三步:插入52，由于50结点只有一个关键字，所以可以插入52
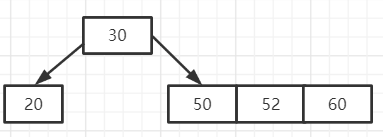
第四步：接下来插入60，插入60之后该结点关键字数量又不符合要求，需要分裂
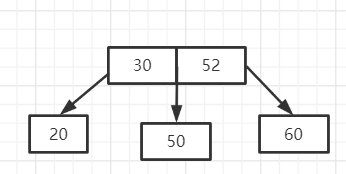
分裂的方法:取中间关键字([3/2]=2)52，由于根结点只含有30一个关键字，可以将52和30合并到一起。接下来需处理50和60这两个结点，由于30<50<52,60>52,所以50和60各自单独作为一个结点。
第五步：接下来插入68，由于60结点只有一个关键字。所以可以插入68
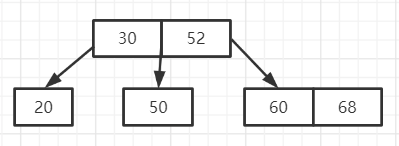
第六步: 接下来插入70，插入70之后该结点关键字数量又不符合要求，需要分裂
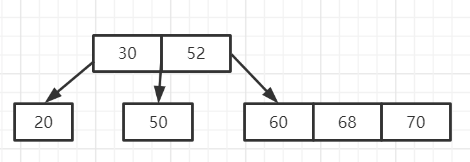
分裂的方法:取中间关键字([3/2]=2)68，由于根结点包含有30和52两个关键字，将68关键字放在根结点后，又需要分裂，又取根结点52，作为新的根结点的关键字。
第一次分裂:
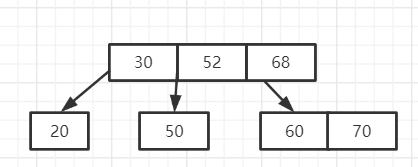
第二次分离(即最终结果):
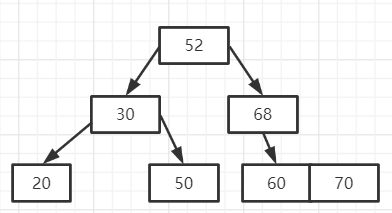
B树的删除操作
B树中的删除操作与插入操作类似，但是稍微复杂些，要使得删除后的结点中的关键字个数>=[m-2]-1,因此将涉及结点的"合并"问题。由于删除的关键字位置不同，可以分为关键字在终端结点和不在终端结点上两种情况。
1）如果删除的关键字在终端结点上(最底层非叶子结点):
- 结点内关键字数量大于[m/2]-1,这时删除这个关键字不会破坏B树的定义要求。所以直接删除。
- 结点内关键字数量等于[m/2]-1,并且其左右兄弟结点中存在关键字数量大于[m/2]-1的结点，则去兄弟结点中借关键字。
- 结点内关键字数量等于[m/2]-1,并且其左右兄弟结点中不存在关键字数量大于[m/2]-1的结点，则需要进行结点合并。
例子:
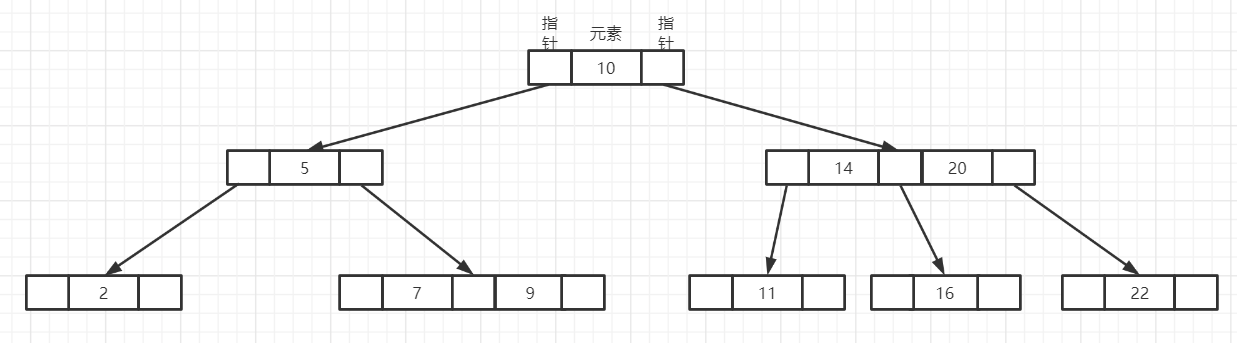
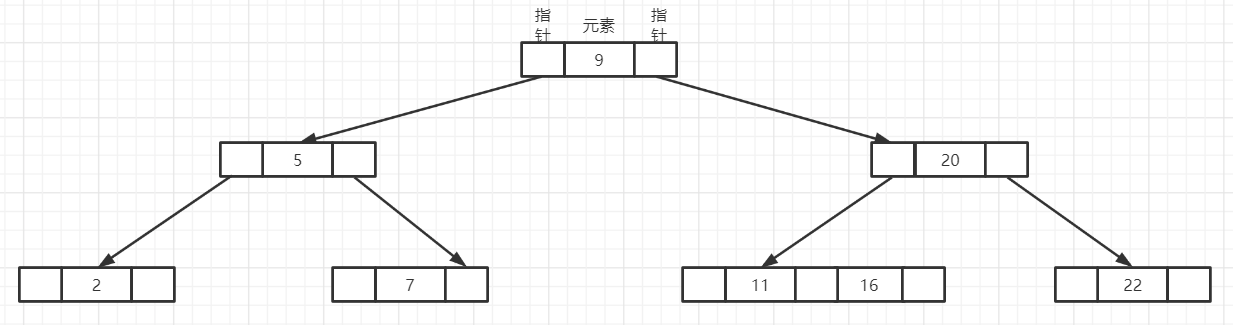
第一种情况: 删除9，直接删除即可。
第二种情况: 删除2，从左右兄借结点，并按照顺序进行整理结点；
- 整理第一步: 将兄弟结点中的最小结点7进行放在上一节点，因为删除的是2，在7的左边；
- 整理第一步: 将父结点中5放入子结点。整理完成后如下图；
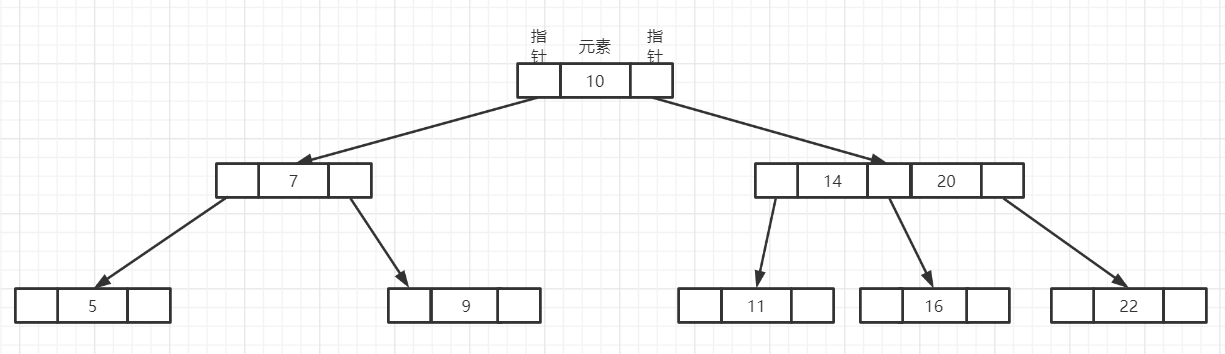
第二种情况: 删除16，左右兄弟结点都只有一个关键字，所以需要进行合并； - 合并第一步: 上一层的结点取关键字与下一层的结点合并。方式不唯一，可以把从把关键字14取下来和11合并成一个结点，也可以把20和22合并成一个结点。
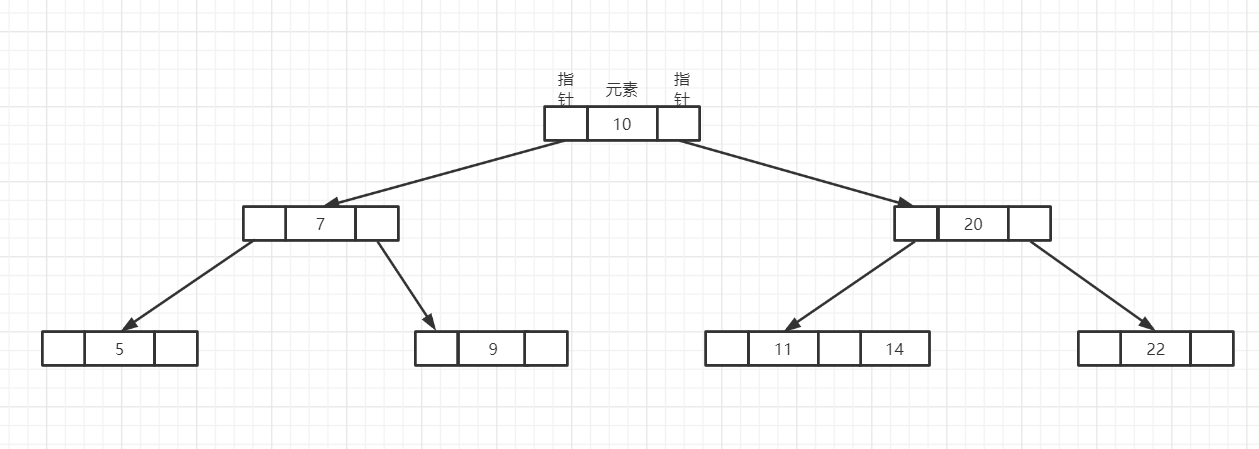
2）如果删除的关键字不在终端结点上(最底层非叶子结点)：需要先转换成再终端结点上，再按照在终端结点上的情况来分别考虑对应的方法。
相邻关键字: 对于不在终端结点上的关键字，它的相邻关键字是其左子树值最大的关键字或者右子树中值最小的关键字。 - 第一种情况：存在关键字数量大于[m/2]-1结点的左子树或右子树，在对应子树上找到该关键字的相邻关键字，然后将相邻关键字替换待删除的关键字。
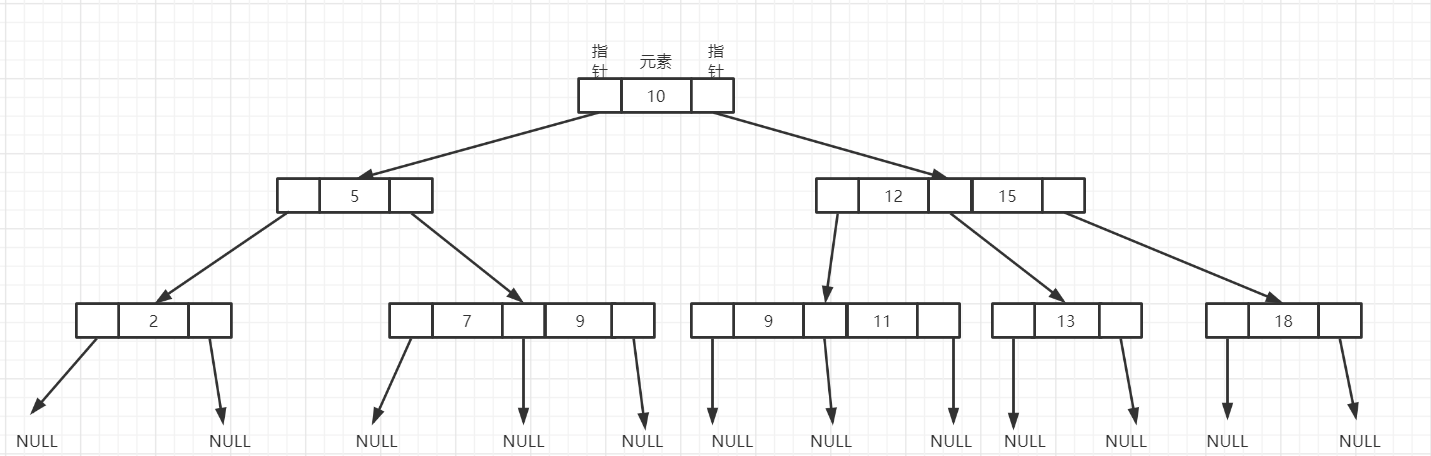
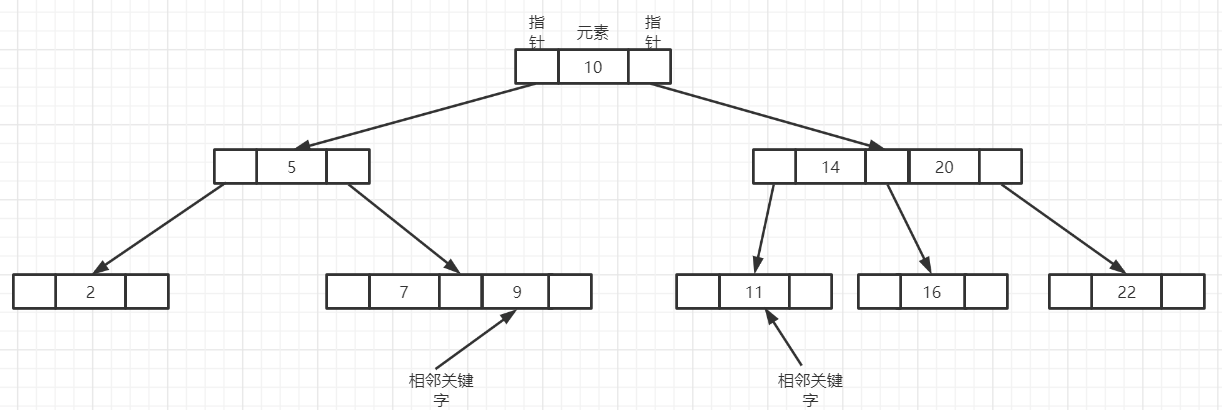
例如: 下图删除10
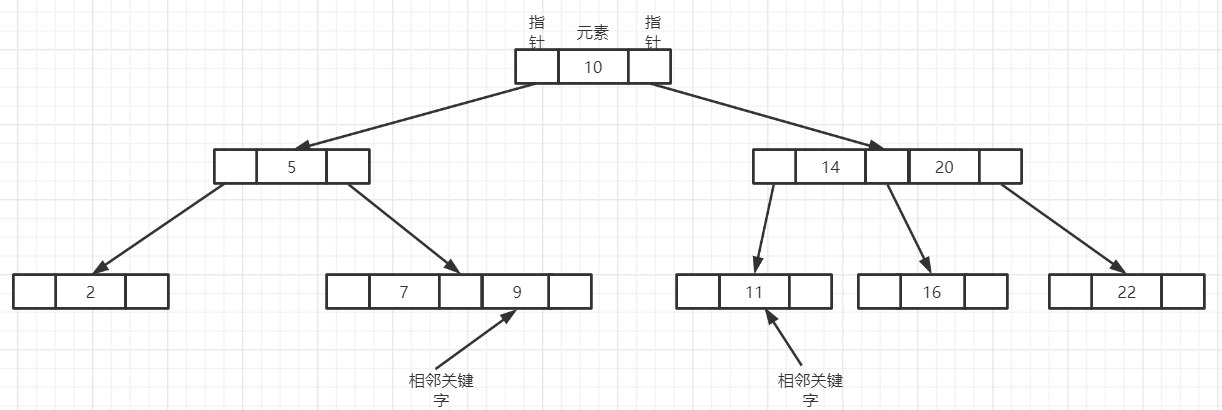
第一步: 找出这个待删除关键字的相邻关键字，比如说下图中10的相邻关键字就是9或者11，其实就是这个大小序列中该关键字的直接前驱或者是直接后驱关键字。
第二步：将这个待删除的关键字和某个相邻关键字互换；互换后，按照关键字在终端结点上的情况进行删除即可。
互换后：
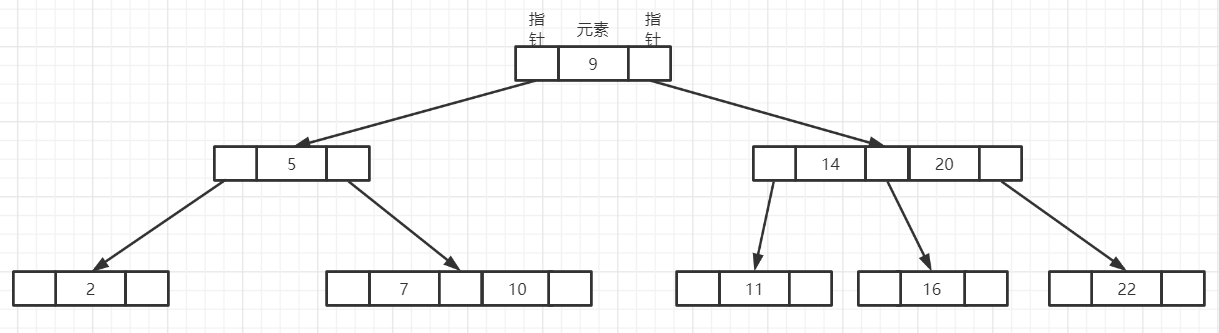
删除后:
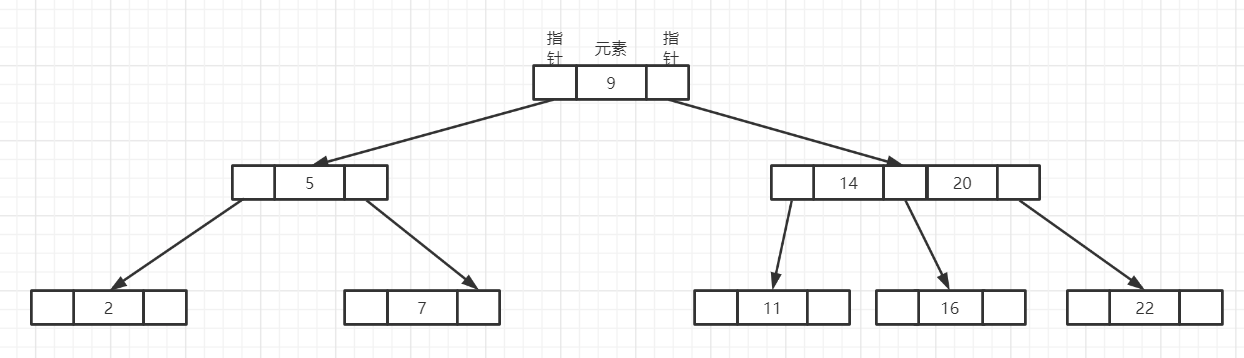
- 第二种情况：左右子树的关键字数量均等于[m/2]-1，则将这两个左右子树结点合并，然后删除待删除关键字。如图删除14
合并后:
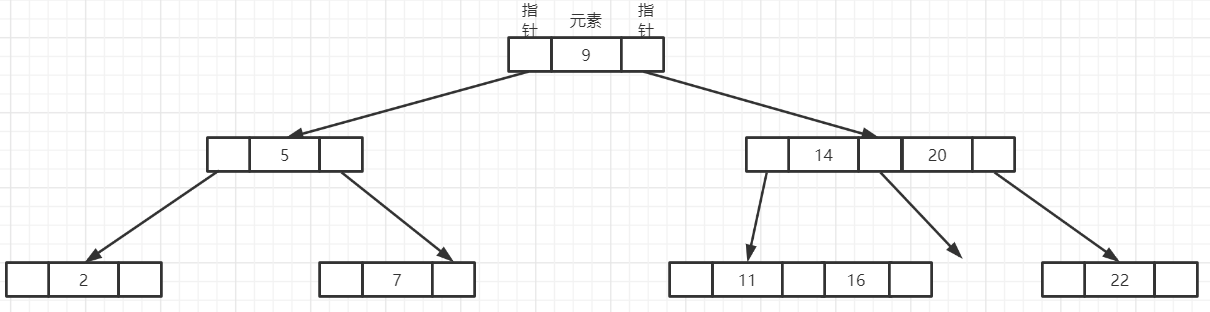
删除后:
B+树
定义
B+树是常用于数据库和操作系统的文件系统中的一种用于查找的数据结构。
B+树图例
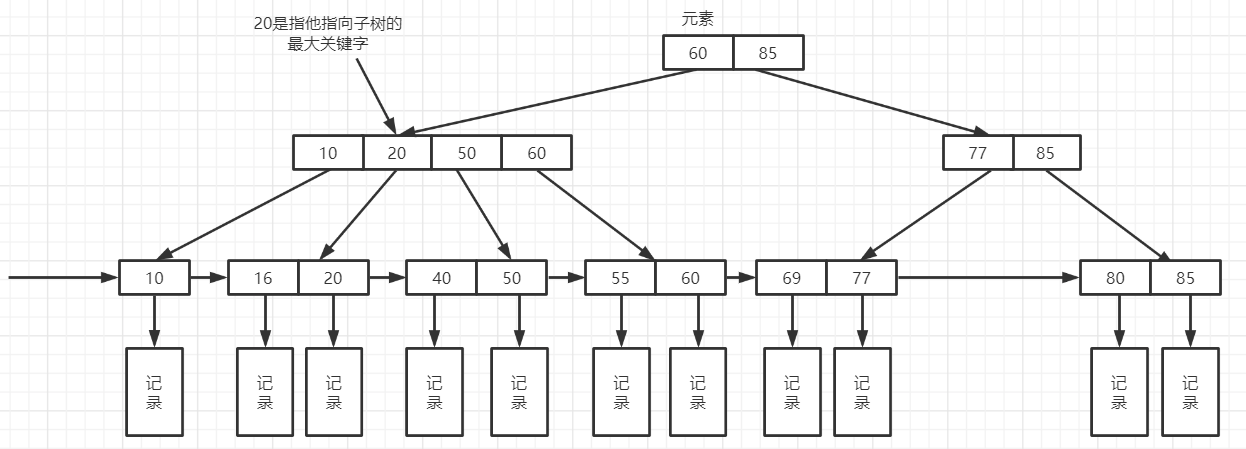
B+tree性质
①：n棵子tree的节点包含n个关键字，不用来保存数据而是保存数据的索引。
②：所有的叶子结点中包含了全部关键字的信息，及指向含这些关键字记录的指针，且叶子结点本身依关键字的大小自小而大顺序链接。
③: 所有的非终端结点可以看成是索引部分，结点中仅含其子树中的大（或小）关键字。
④：B+树中，数据对象的插入和删除仅在叶节点上进行。
⑤：B+树有2个头指针，一个是树的根节点，一个是小关键码的叶节点。
B+树和B树的区别
①：在B+树中，具有n个关键字的结点只含有n棵子树，即每个关键字对应一颗子树；而在B树中，具有n个关键字的结点含有(n+1)棵子树。
②：在B+树中，每个结点(非根内部结点)关键字个数n的范围是[m/2]<=n<=m(根结点1<=n<=m),在B树中，每个结点(非根内部结点)关键字个数n的范围是[m/2]-1<=n<=m-1(根结点:1<=n<=m-1)。
③: 在B+树中，叶结点包含信息，所有非叶结点仅起到索引的作用，非叶结点中的每个索引项只含有对应子树的最大关键字和指向该子树的指针，不含有该关键字对应的存储地址。
④：在B+树中，叶结点包含了全部关键字，即在非叶结点中出现的关键字也会出现在叶结点中；而在B树中，叶结点包含的关键字和其他结点包含的关键字是不重复的。
⑤：在B+树中，有一个指针指向关键字最小的叶子结点，所有叶子结点连接成一个单链表。
