java实现二叉查找树与AVL树
一、基本知识
(1)、树的概念
二叉树:一棵树中每个节点都不能有多于两个以上的儿子节点。
二叉查找树:对于树中的每一个节点x,它的左子树中所有项的值均小于x节点的值,而它的右子树中所有项的值均大于x节点的值。
AVL树:每个节点的左子树和右子树的高度最多差1的二叉查找树(空树的高度为-1)。
节点的高度:从节点到一个叶子节点的最大长度。(叶子节点是没有儿子的节点)
树的高度:从根节点开始到叶子节点的最大长度。
(2)、树的遍历
树的遍历分为三种:中序遍历,先序遍历,后序遍历。
先序:从根节点开始,对于每个节点的处理都在它的诸多儿子节点之前处理,按照根,左,右的顺序。
后序:从根节点开始,对于每个节点的处理都在它的诸多儿子节点之后处理,按照左,右,根的顺序。
中序:从根节点开始,对于每个节点的处理都要在它的左儿子节点处理之后,右儿子节点处理之前,按照左,根,右的顺序。
(1、把每个即将要处理的节点当成根节点2、如果某个节点为空,则视为已处理)
例: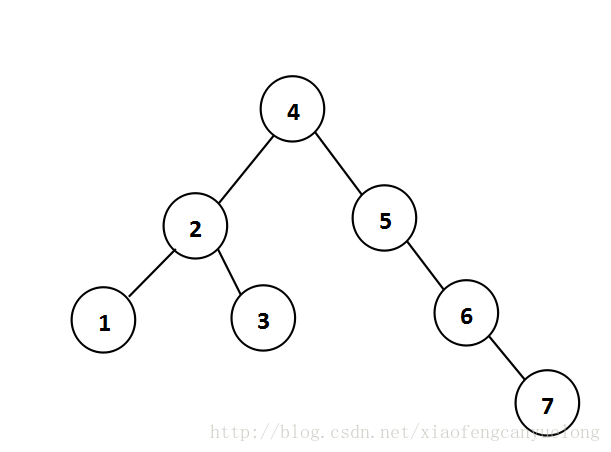
先序遍历:4213567
中序遍历:1234567
后序遍历:7653124
(3)、二叉查找树与AVL树的区分
如上图中的树,它每个节点的儿子个数最多为2,且每个节点的左子树的值均小于该节点的值,右子树的值均大于该节点的值,则它是个二叉查找树。
AVL树讲的是每个节点的左子树的高度与右子树的高度最多差1的二叉查找树。
图中的树的节点5的左子树的高度为-1(空树),右子树的高度为1,故差值为2>1,则它不是个AVL树。
(4)、AVL树的平衡
我们把需要平衡的节点叫做α,如上图中节点5就是α节点。引起α节点的不平衡(左右子树的高度差大于1)有四种情况。
1.对α的左儿子的左子树进行一次插入。
2.对α的左儿子的右子树进行一次插入。
3.对α的右儿子的左子树进行一次插入。
4.对α的右儿子的右子树进行一次插入。
如图中就是对节点5的右儿子的右子树进行一次插入(插入的是7)
对于这四种不平衡的情况,可通过单旋转和双旋转来完成平衡。
单旋转适用于1,4两种情况
举例:
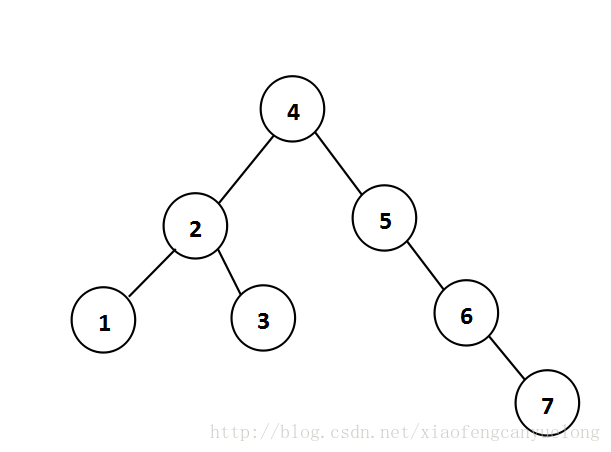
该图中的节点5是不平衡的,它的不平衡情况是4,可使用单旋转来完成节点5的平衡。
进行单旋转后:
双旋转适用于2,3两种情况
举例:
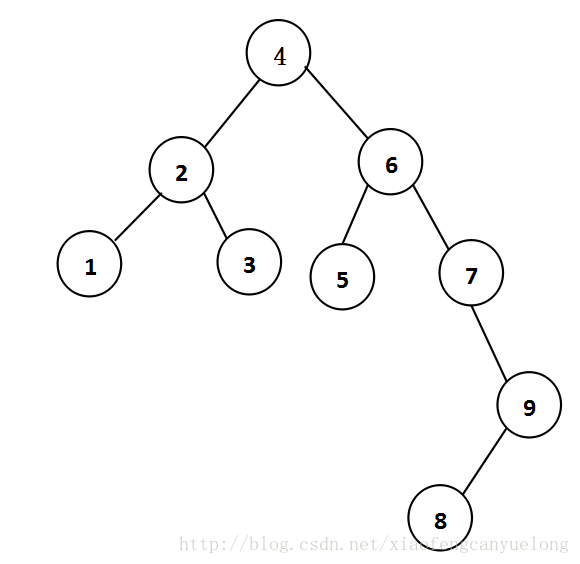
图中的节点7发生了不平衡,它的不平衡情况是3,可是要双旋转来完成节点7的平衡。
二、实现代码
(1)、二叉查找树
//二叉查找树---泛型类
public class BinarySearchTree<AnyType extends Comparable<? super AnyType>> {
private BinaryNode<AnyType> root;// 根节点
public BinarySearchTree() {
root = null;
}
// 置空
public void makeEmpty() {
root = null;
}
// 判断是否为null
public boolean isEmpty() {
return root == null;
}
// 判断某树种是否含有元素x
public boolean contains(AnyType x) {
return contains(x, root);
}
// 找到树中最小的元素并返回
public AnyType findMin() throws Exception {
if (isEmpty()) {
throw new Exception();
}
return findMin(root).element;
}
// 找到树中最大的元素并返回
public AnyType findMax() throws Exception {
if (isEmpty()) {
throw new Exception();
}
return findMax(root).element;
}
// 插入元素x
public void insert(AnyType x) {
root = insert(x, root);
}
// 移除元素x
public void remove(AnyType x) {
root = remove(x, root);
}
// 打印树
public void printTree() {
if (isEmpty()) {
System.out.println("空树");
} else {
printTree(root);
}
}
// 打印树----》按照中序遍历输出树
private void printTree(BinaryNode<AnyType> node) {
if (node != null) {
printTree(node.left);
System.out.print(node.element + " ");
printTree(node.right);
}
}
// 移除某节点
private BinaryNode<AnyType> remove(AnyType x, BinaryNode<AnyType> node) {
if (node == null) {// 没找到
return node;
}
int compareResult = x.compareTo(node.element);
if (compareResult < 0) {
node.left = remove(x, node.left);
} else if (compareResult > 0) {
node.right = remove(x, node.right);
// 找到了该节点
} else if (node.left != null && node.right != null) {// 该节点有两个孩子节点
node.element = findMin(node.right).element;
node.right = remove(node.element, node.right);
} else {// 该节点只有一个孩子节点
node = (node.left != null) ? node.left : node.right;
}
return node;
}
// 插入元素x,并返回节点
private BinaryNode<AnyType> insert(AnyType x, BinaryNode<AnyType> node) {
// 树为空,新建一个树,并插入元素x
if (node == null) {
return new BinaryNode<AnyType>(x, null, null);
}
int compareResult = x.compareTo(node.element);
if (compareResult < 0) {
node.left = insert(x, node.left);
} else if (compareResult > 0) {
node.right = insert(x, node.right);
} else {
;
}
}
return node;
}
// 根据树的性质,树中最大的元素位于树的最右侧
private BinaryNode<AnyType> findMax(BinaryNode<AnyType> node) {
if (node != null) {
while (node.right != null) {
node = node.right;
}
}
return node;
}
// 根据查找树的性质,最小的元素处于最左边
private BinaryNode<AnyType> findMin(BinaryNode<AnyType> node) {
if (node == null) {
return null;
} else if (node.left == null) {
return node;
}
return findMin(node.left);
}
// 查找某元素x
private boolean contains(AnyType x, BinaryNode<AnyType> node) {
if (node == null) {
return false;
}
int compareResult = x.compareTo(node.element);
if (compareResult < 0) {//小于该节点
return contains(x, node.left);// 到该节点的左子树中寻找
} else if (compareResult > 0) {
return contains(x, node.right);// 到该节点的右子树中寻找
} else {
return true;
}
}
// 节点类---内部类
private static class BinaryNode<AnyType> {
AnyType element;//值
BinaryNode<AnyType> left;//左孩子节点
BinaryNode<AnyType> right;//右孩子节点
public BinaryNode(AnyType element) {
this(element, null, null);
}
public BinaryNode(AnyType theElement, BinaryNode<AnyType> lNode, BinaryNode<AnyType> rNode) {
element = theElement;
left = lNode;
right = rNode;
}
}
public static void main(String[] args) {
BinarySearchTree<Integer> tree = new BinarySearchTree<>();
tree.insert(6);
tree.insert(3);
tree.insert(8);
tree.insert(1);
tree.insert(4);
/*
* 中序 1 3 4 6 8
*/
tree.printTree();
}
}
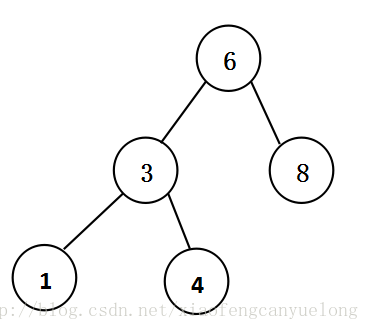
上述代码中的测试树:
(2)、AVL树
//Avl树
public class AvlTree<AnyType extends Comparable<? super AnyType>> {
private static final int ALLOWED_IMBALANCE = 1;
private AvlNode<AnyType> root;// 根节点
public AvlTree() {
root = null;
}
// 置空
public void makeEmpty() {
root = null;
}
// 判断是否为null
public boolean isEmpty() {
return root == null;
}
// 判断某树种是否含有元素x
public boolean contains(AnyType x) {
return contains(x, root);
}
// 找到树中最小的元素并返回
public AnyType findMin() throws Exception {
if (isEmpty()) {
throw new Exception();
}
return findMin(root).element;
}
// 找到树中最大的元素并返回
public AnyType findMax() throws Exception {
if (isEmpty()) {
throw new Exception();
}
return findMax(root).element;
}
// 插入元素x
public void insert(AnyType x) {
root = insert(x, root);
}
// 移除元素x
public void remove(AnyType x) {
root = remove(x, root);
}
// 打印树
public void printTree() {
if (isEmpty()) {
System.out.println("空树");
} else {
printTree(root);
}
}
// 打印树----》中序遍历
private void printTree(AvlNode<AnyType> node) {
if (node != null) {
printTree(node.leftNode);
System.out.print(node.element + " ");
printTree(node.rightNode);
}
}
// 返回树的高度
private int height(AvlNode<AnyType> node) {
return node == null ? -1 : node.height;
}
// 插入一个x节点到树中
private AvlNode<AnyType> insert(AnyType x, AvlNode<AnyType> node) {
if (node == null) {
return new AvlNode<AnyType>(x, null, null);
}
int compareResult = x.compareTo(node.element);
if (compareResult < 0) {
node.leftNode = insert(x, node.leftNode);
} else if (compareResult > 0) {
node.rightNode = insert(x, node.rightNode);
} else {
;
}
return balance(node);// 进行树的平衡
}
// 进行树的平衡
private AvlNode<AnyType> balance(AvlNode<AnyType> node) {
if (node == null) {
return node;
}
// 左子树和右子树的高度差超过1
if (height(node.leftNode) - height(node.rightNode) > ALLOWED_IMBALANCE) {
if (height(node.leftNode.leftNode) >= height(node.leftNode.rightNode)) {
node = rotateWithLeftChild(node);
} else {
node = doubleWithLeftChild(node);
}
} else {
if (height(node.rightNode) - height(node.rightNode) > ALLOWED_IMBALANCE) {
if (height(node.rightNode.rightNode) >= height(node.rightNode.leftNode)) {
node = rotateWithRightChild(node);
} else {
node = doubleWithRightChild(node);
}
}
}
node.height = Math.max(height(node.leftNode), height(node.rightNode));
return node;
}
// 移除x节点
private AvlNode<AnyType> remove(AnyType x, AvlNode<AnyType> node) {
if (node == null) {
return node;
}
int compareResult = x.compareTo(node.element);
if (compareResult < 0) {
node.leftNode = remove(x, node.leftNode);
} else if (compareResult > 0) {
node.rightNode = remove(x, node.rightNode);
} else if (node.leftNode != null && node.rightNode != null) {
node.element = findMin(node.rightNode).element;
node.rightNode = remove(node.element, node.rightNode);
} else {
node = (node.leftNode != null) ? node.leftNode : node.rightNode;
}
return balance(node);
}
// 单旋转--->对应不平衡情况:--->左子树的左节点的高度大于左子树的右节点的高度
private AvlNode<AnyType> rotateWithLeftChild(AvlNode<AnyType> k2) {
AvlNode<AnyType> k1 = k2.leftNode;
k2.leftNode = k1.rightNode;
k1.rightNode = k2;
k2.height = Math.max(height(k2.leftNode), height(k2.rightNode)) + 1;
k1.height = Math.max(height(k1.leftNode), k2.height) + 1;
return k1;
}
// 单旋转--->对应不平衡情况:--->右子树的右节点的高度大于右子树的左节点的高度
private AvlNode<AnyType> rotateWithRightChild(AvlNode<AnyType> k2) {
AvlNode<AnyType> k1 = k2.rightNode;
k2.rightNode = k1.leftNode;
k1.leftNode = k2;
k2.height = Math.max(height(k2.rightNode), height(k2.leftNode)) + 1;
k1.height = Math.max(height(k1.rightNode), k2.height) + 1;
return k1;
}
// 双旋转--->对应不平衡情况:--->左子树的左节点的高度小于左子树的右节点的高度
private AvlNode<AnyType> doubleWithLeftChild(AvlNode<AnyType> k3) {
k3.leftNode = rotateWithLeftChild(k3.leftNode);
return rotateWithLeftChild(k3);
}
// 双旋转--->对应不平衡情况:--->右子树的右节点的高度小于右子树的右节点的高度
private AvlNode<AnyType> doubleWithRightChild(AvlNode<AnyType> k3) {
k3.rightNode = rotateWithLeftChild(k3.rightNode);
return rotateWithLeftChild(k3);
}
// 根据树的性质,树中最大的元素位于树的最右侧
private AvlNode<AnyType> findMax(AvlNode<AnyType> node) {
if (node != null) {
while (node.rightNode != null) {
node = node.rightNode;
}
}
return node;
}
// 根据查找树的性质,最小的元素处于最左边
private AvlNode<AnyType> findMin(AvlNode<AnyType> node) {
if (node == null) {
return null;
} else if (node.leftNode == null) {
return node;
}
return findMin(node.leftNode);
}
// 查找某元素x
private boolean contains(AnyType x, AvlNode<AnyType> node) {
if (node == null) {
return false;
}
int compareResult = x.compareTo(node.element);
if (compareResult < 0) {
return contains(x, node.leftNode);// 查找左子树
} else if (compareResult > 0) {
return contains(x, node.rightNode);// 查找右子树
} else {
return true;
}
}
// 节点类---内部类
private static class AvlNode<AnyType> {
AnyType element;
AvlNode<AnyType> leftNode;
AvlNode<AnyType> rightNode;
int height;//节点对应的高度
public AvlNode(AnyType element) {
this(element, null, null);
}
public AvlNode(AnyType theElment, AvlNode<AnyType> lNode, AvlNode<AnyType> rNode) {
element = theElment;
leftNode = lNode;
rightNode = rNode;
height = 0;
}
}
public static void main(String[] args) {
AvlTree<Integer> tree = new AvlTree<>();
tree.insert(4);
tree.insert(5);
tree.insert(2);
tree.insert(1);
tree.insert(3);
tree.insert(6);
tree.insert(7);
tree.printTree();//1 2 3 4 5 6 7
}
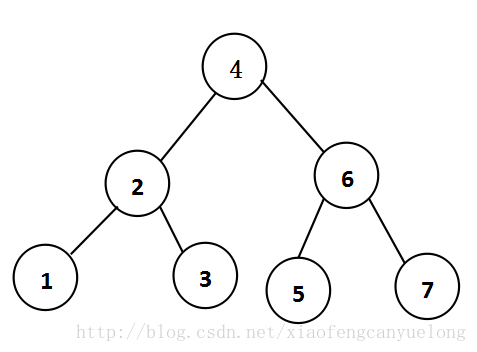
}在Main方法中,创建了AvlTree并且插入4,5,2,1,3,6,7节点,最后按树的中序打印出的是1 2 3 4 5 6 7 ,这说明此时树的结构为:
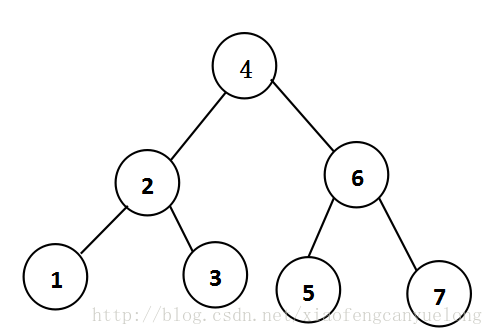
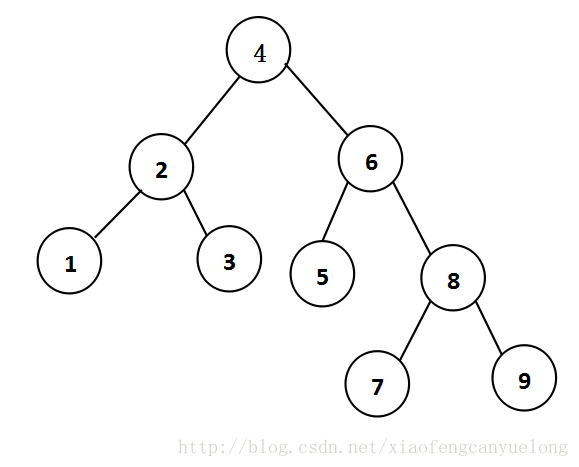
而不是
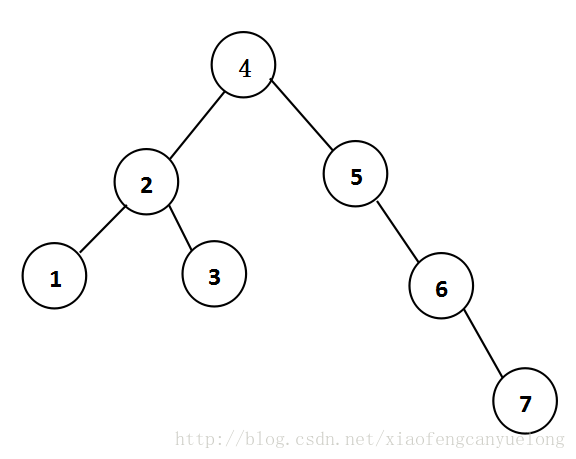
这就说明在插入节点时如果某节点发生了不平衡,则根据产生不平衡的情况来进行单旋转或双旋转操作,从而完成该节点的平衡。上述例子中是节点5处发生了不平衡,进行了单旋转操作来实现了节点5的平衡。
The world won’t care about your self-esteem.The world will expect you to accomplish something before you feel good about yourself.