一个四则运算的小程序

代码地址https://coding.net/u/huhulong/p/sizeyunsuan/git/tree/master/

（一）需求分析

1. 控制题目生成个数

2. 可以控制题目生成数的范围

3. 生成的题目中如果存在形如e1 ÷ e2的子表达式，那么其结果应是真分数。

4. 每道题目中出现的运算符个数不超过3个。

5. 程序一次运行生成的题目不能重复，即任何两道题目不能通过有限次交换+和×左右的算术表达式变换为同一道题目。

生成的题目存入执行程序的当前目录下的Exercises.txt文件，格式如下：

     1. 四则运算题目1

     2. 四则运算题目2

          ……

其中真分数在输入输出时采用如下格式，真分数五分之三表示为3/5，真分数二又八分之三表示为2’3/8。

6. 在生成题目的同时，计算出所有题目的答案，并存入执行程序的当前目录下的Answers.txt文件，格式如下：

    1. 答案1

    2. 答案2

 

    特别的，真分数的运算如下例所示：1/6 + 1/8 = 7/24。

7. 程序应能支持一万道题目的生成。

8. 程序支持对给定的题目文件和答案文件，判定答案中的对错并进行数量统计，并会输出所有题目中重复的题目，输入参数如下：

     Myapp.exe -e <exercisefile>.txt -a <answerfile>.txt -o Grade.txt

 

统计结果输出到文件Grade.txt，格式如下：

 

Correct: 5 (1, 3, 5, 7, 9)

Wrong: 5 (2, 4, 6, 8, 10)

Repeat:2

RepeatDetail:

(1)   2,45+32  Repeat 3,32+45                    

(2)   5,3+(2+1)  Repeat 7,1+2+3

 

（二）功能设计

 　　基本功能：

（1）在控制台可以控制生成的题目的数量和范围，并且将题目和答案分别写入到两个文件当中。

（2）使用者可以在给定的文件夹中写上题目答案，在控制台用某个操作可以得出其结果

（3）出现重复的题目可以在grade文件中看到

 

（三）设计实现

首先，这是我的目录结构

 

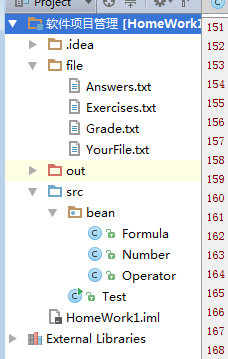
其中，模型类有Number类，实例成员变量有整数部分，分子，分母

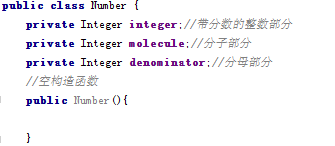
这三个组成一个带分数，并且用构造方法

实现自动生成不小于自然数upperLimit的带分数。

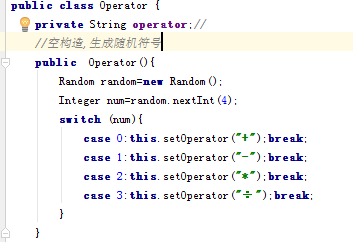
然后是符号类，这个类比较简单，只有一个实例变量，该实例变量代表着四则运算的四种符号，并且在类里头定义了随机生成四种运算符的构造方法

接着是式子类Formula，我给他定义了两个List类型的实例变量，一个numberList存放一个式子的所有随机生成带分数，另一个operatorList存放式子中所有的算符，

并且定义了随机生成若干个带分数和算符组合起来的构造方法，将生成的带分数和算符分别存入到实例变量中，

 

我在该类中定义了两个实例方法，

第一个是将数列表和符号列表组合成式子的方法

第二个是计算该式子结果的方法

最后一个类是主类Test类，我将对文件的操作都放在主类中进行。

然后是四个文件夹，

Exercises.txt:生成题目文件夹

Answers.txt：生成答案文件夹

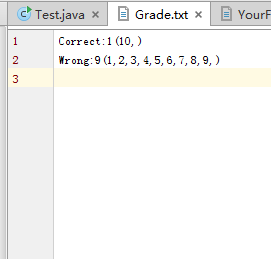
Grade.txt：成绩展示文件夹

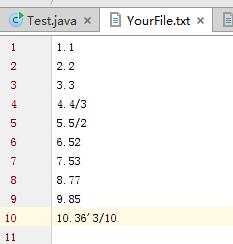
YourFile.txt：使用者将答案写在该文件夹中

（四）代码说明

1.生成随机数算法

本身该算法并不难，但是要排除三种情况，第一种是带分数的整数部分为0的情况，就只展示分数部分，第二种是分数部分的分子和分母相同，这时候整数部分+1，并且不展示

分数部分，第三种情况是分子为0，此时分数部分不展示，只展示整数部分。

 

2.生成四则算式并将其转换为字符串的方法

由于算式都是“算符数量=带分数数量-1”，所以我们明白在列表中一个算符的前一个数和后一个数相对于该算符在列表中的下标是x和x+1(x代表某个算符在列表中的位置)。

3.算式答案生成算法

思路是这样：

由于乘算和除算的优先级高于加减，所以需要先对按顺序对式子的乘算和除算先进行计算后才能对式子的加减算进行计算

举个例子，式子的实例变量两个列表，一个存放数字，一个存放算符

第一次计算时

numberList:   5 ,10 , 15 , 20;

operatorList:    +.    * ,    ÷

先进行乘除检测，从operatorList中检测，检测到列表下标1为“*”，此时，取到numberList中的下标为1和2的数，并把他们相乘，得到150的结果，并且把他们放入numberList的10前面，然后去掉10，15两个数，同样的，把operatorList中的“*”符remove掉

第二次计算时

NumberList：5  ,  150  ，  20；

operatorList：+，÷

乘除检测还在继续，此时检测到÷符，根据第一次方法的方式，此时剩下一个算符

第三次计算

numberList：5  ，7’1/2；

operatorList： +

乘除算法的结束情况为当operator列表中不存在乘除符号，此时进行加减算法，并得到最后结果

numberList：12’1/2；

operator：空

此时得到算式结果为12’1/2；

使用这样的思路，无论算符有多少个，都可以用该方法算出结果。

//生成式子答案
public Number getAnswser() {
    //先对式子的*和÷进行处理
    int i = 0;
    while (i < operatorList.size()) {
        //如果数列里的数个数是0，则返回该方法
        if (numberList.size()==1){
            return (Number) numberList.get(0);
        }
        //当算符出现*和÷的时候
        if (operatorList.get(i).equals("*") || operatorList.get(i).equals("÷")) {
            //取得运算符两侧的数
            Number numberFront = (Number) numberList.get(i);
            Number numberAfter = (Number) numberList.get(i + 1);
            //求得运算符两侧数值的分子部分
            int numberFrontMolecule = numberFront.getInteger() * numberFront.getDenominator() + numberFront.getMolecule();
            int numberAfterMolecule = numberAfter.getInteger() * numberAfter.getDenominator() + numberAfter.getMolecule();
            int endMolecule = 0;
            int endDenominator = 0;
            //算得两数相乘的分子值和分母值
            if (operatorList.get(i).equals("*")) {
                endMolecule = numberFrontMolecule * numberAfterMolecule;
                endDenominator = numberFront.getDenominator() * numberAfter.getDenominator();
            }
            if (operatorList.get(i).equals("÷")) {
                endMolecule = numberFrontMolecule * numberAfter.getDenominator();
                endDenominator = numberAfterMolecule * numberFront.getDenominator();
            }
            int endInteger = 0;//初始分子的整数部分为0
            if (endMolecule > endDenominator) {
                endInteger = endMolecule / endDenominator;
                endMolecule = endMolecule % endDenominator;
            }
            //求最大公约数
            int smaller = endMolecule > endDenominator ? endMolecule : endDenominator;
            int maxCommonFactor = 1;
            for (int j = 1; j <= smaller; j++) {
                if (endMolecule % j == 0 && endDenominator % j == 0) {
                    maxCommonFactor = j;
                }
            }
            endMolecule = endMolecule / maxCommonFactor;
            endDenominator = endDenominator / maxCommonFactor;
            Number endNumber = new Number(endInteger, endMolecule, endDenominator);//约分后的式子
            this.numberList.add(i, endNumber);
            this.numberList.remove(i + 1);
            this.numberList.remove(i + 1);
            this.operatorList.remove(i);
        }else {
            i++;
        }
    }

    //进行完*÷处理后进行+-处理
    while (operatorList.size()!=0){
        //取得运算符两侧的数
        Number numberFront = (Number) numberList.get(0);
        Number numberAfter = (Number) numberList.get(1);
        //求得运算符两侧数值的分子部分
        int numberFrontMolecule = numberFront.getInteger() * numberFront.getDenominator() + numberFront.getMolecule();
        int numberAfterMolecule = numberAfter.getInteger() * numberAfter.getDenominator() + numberAfter.getMolecule();
        //不管两式子的分母一样或不一样，都把两分母相乘
        int endDenominator=numberFront.getDenominator()*numberAfter.getDenominator();
        //如果为+符，就进行+算
        int allMolecule1=numberFrontMolecule*numberAfter.getDenominator();
        int allMolecule2=numberAfterMolecule*numberFront.getDenominator();
        int endMolecule=0;//定义未约分前的分子部分
        if (operatorList.get(0).equals("+")){
            endMolecule=allMolecule1+allMolecule2;
        }
        if (operatorList.get(0).equals("-")){
            endMolecule=allMolecule1-allMolecule2;
        }
        int endInteger = 0;//初始分子的整数部分为0
        if (endMolecule > endDenominator) {
            endInteger = endMolecule / endDenominator;
            endMolecule = endMolecule % endDenominator;
        }
        //求最大公约数
        int smaller = endMolecule > endDenominator ? endMolecule : endDenominator;
        int maxCommonFactor = 1;
        for (int j = 1; j <= smaller; j++) {
            if (endMolecule % j == 0 && endDenominator % j == 0) {
                maxCommonFactor = j;
            }
        }
        endMolecule = endMolecule / maxCommonFactor;
        endDenominator = endDenominator / maxCommonFactor;
        Number endNumber = new Number(endInteger, endMolecule, endDenominator);//约分后的式子
        this.numberList.add(0, endNumber);
        this.numberList.remove(1);
        this.numberList.remove(1);
        this.operatorList.remove(0);
    }
    return (Number) numberList.get(0);
}

 （五）测试运行

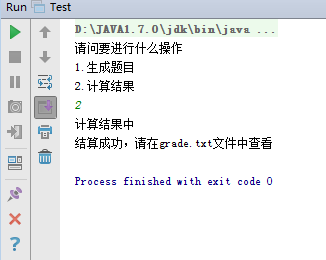
1.生成题目

Test主函数：                                                                         Exercises.txt文件夹：                                                 Answers.txt文件夹

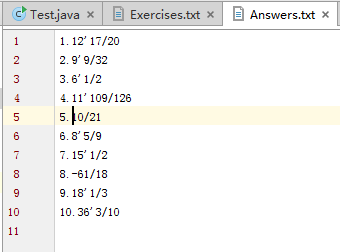
2.检测题目对错

YourFile.txt文件夹　　　　　　　　　　主函数Test 　　　　　　　　　　　　　　　　　　　　Grade.txt文件夹

           

（六）PSP展示

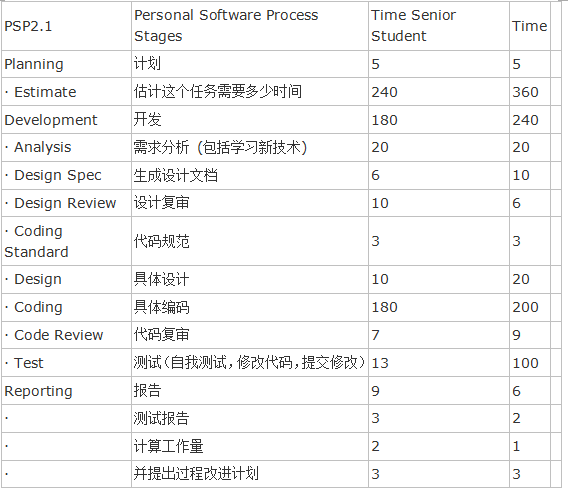
（七）小结

其实如果打代码时思路清晰的话，编码的时间应该不会很长，但是有些细节可能会导致程序出bug，后面调bug的时间也用了非常长的时间。

然后说说此次作业遇到的一些坑，一个是文件的写入操作，如果没有使用flush，写入操作是不会进行的，感觉当初学习java时没有太深入得去理解，总是觉得flush和close绑定起来用，没有去注意它主要的作用是什么，

然后是对列表的操作，由于在计算结果的算法中，需要对列表中的值进行添加和删除，会造成列表的下标和长度发生变动，一不注意就容易出现数组越界的异常。

然后就是对重复性检测的一些思路，

1.读取题目文件，并且用一个列表来存放读取到的字符串

2.对该列表进行操作，取出每个列表中的成员，并且进行如下操作：

　　（1）用字符串的CharAt方法，一步步读至算符，算符前面的部分作为分数/带分数/整数部分存入List列表中，将算符存入到另一个operatorList列表中

　　（2）将读取的数值部分根据读到的 ’ 和 /符号，将数值部分分成整数部分和分子，分母部分，存入到numberList列表中

　　（3）重复（1）（2）部分，即可将文件中读到的式子全部转换成一个个的算式对象（算式对象中有operatorList和numberList两个实例变量）

　　（4）根据÷和-号两边不可变，*和+号两边可以变动来判断两个式子的重复性。