二叉搜索树的后序遍历序列
问题描述
输入一个整数数组，判断该数组是不是某二叉搜索树的后序遍历结果。如果是则返回 true，否则返回 false。假设输入的数组的任意两个数字都互不相同。
参考以下这颗二叉搜索树：
5 / \ 2 6 / \ 1 3
示例 1：
输入: [1,6,3,2,5] 输出: false
示例 2：
输入: [1,3,2,6,5] 输出: true
提示：数组长度 <= 1000
解法一（递归）：
如果这题说的是判断该数组是不是某二叉树的中序遍历结果，那么这道题就非常的简单了，因为二叉树搜索树的中序遍历结果一定是有序的，我们只需要判断数组是否有序就行了，但这道题要判断的是不是某二叉搜索树的后序遍历结果，这样就有点难办了。
二叉搜索树的特点是左子树的值<根节点<右子树的值。而后续遍历的顺序是：左子节点→右子节点→根节点；
比如下面这棵二叉树，他的后续遍历是
[3，5，4，10，12，9]
我们知道后续遍历的最后一个数字一定是根节点，所以数组中最后一个数字9就是根节点，我们从前往后找到第一个比9大的数字10，那么10后面的[10，12]（除了9）都是9的右子节点，10前面的[3，5，4]都是9的左子节点，后面的需要判断一下，如果有小于9的，说明不是二叉搜索树，直接返回false。然后再以递归的方式判断左右子树。
再来看一个，他的后续遍历是[3，5，13，10，12，9]
我们来根据数组拆分，第一个比9大的后面都是9的右子节点[13，10，12]。然后再拆分这个数组，12是根节点，第一个比12大的后面都是12的右子节点[13，10]，但我们看到10是比12小的，他不可能是12的右子节点，所以我们能确定这棵树不是二叉搜索树。搞懂了上面的原理我们再来看下代码。
public boolean verifyPostorder(int[] postorder){
return helper(postorder, 0, postorder.length - 1);
}
private boolean helper(int[] postorder, int left, int right) {
//如果left==right，就一个节点不需要判断了，如果left>right说明没有节点，
//也不用再看了,否则就要继续往下判断
if (left>=right)return true;
//因为数组中最后一个值postorder[right]是根节点，这里从左往右找出第一个比
// 根节点大的值，他后面的都是根节点的右子节点（包含当前值，不包含最后一个值，
//因为最后一个是根节点），他前面的都是根节点的左子节点
int mid = left;
//根节点
int root = postorder[right];
//找到左右节点临界点
while (postorder[mid] < root)
mid++;
int temp = mid;
//因为postorder[mid]前面的值都是比根节点root小的，
//我们还需要确定postorder[mid]后面的值都要比根节点root大，
//如果后面有比根节点小的直接返回false
while (temp < right) {
if (postorder[temp++] < root)
return false;
}
//然后对左右子节点进行递归调用
return helper(postorder,left,mid-1)&&helper(postorder,mid,right-1);
}
解法二（迭代）：
我们先来画一个节点多一些的二叉搜索树，然后观察一下他的规律
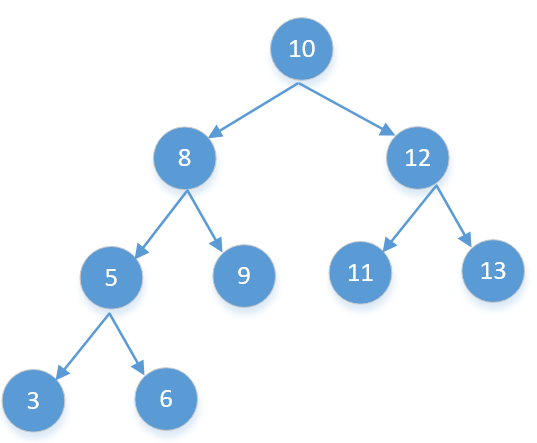
他的后续遍历结果是
[3,6,5,9,8,11,13,12,10]
从前往后不好看，我们来从后往前看
[10,12,13,11,8,9,5,6,3]
如果你仔细观察会发现一个规律，就是挨着的两个数如果arr[i]<arr[i+1]，那么arr[i+1]一定是arr[i]的右子节点，这一点是毋庸置疑的，，我们可以看下上面的10和12是挨着的并且10<12，所以12是10的右子节点。同理12和13，8和9，5和6，他们都是挨着的，并且前面的都是小于后面的，所以后面的都是前面的右子节点。如果想证明也很简单，因为比arr[i]大的肯定都是他的右子节点，如果还是挨着他的，肯定是在后续遍历中所有的右子节点最后一个遍历的，所以他一定是arr[i]的右子节点。
我们刚才看的是升序的，再来看一下降序的（这里的升序和降序都是基于后续遍历从后往前看的，也就是上面的数组）。
如果arr[i]>arr[i+1]，那么arr[i+1]一定是arr[0]……arr[i]中某个节点的左子节点，并且这个值是大于arr[i+1]中最小的。我们来看一下上面的数组，比如13，11是降序的，那么11肯定是他前面某一个节点的左子节点，并且这个值是大于11中最小的，我们看到12和13都是大于11的，但12最小，所以11就是12的左子节点。同理我们可以观察到11和8是降序，8前面大于8中最小的是10，所以8就是10的左子节点。9和5是降序，6和3是降序，都遵守这个规律。
根据上面分析的过程，很容易想到使用栈来解决。遍历数组的所有元素，如果栈为空，就把当前元素压栈。如果栈不为空，并且当前元素大于栈顶元素，说明是升序的，那么就说明当前元素是栈顶元素的右子节点，就把当前元素压栈，如果一直升序，就一直压栈。当前元素小于栈顶元素，说明是倒序的，说明当前元素是某个节点的左子节点，我们目的是要找到这个左子节点的父节点，就让栈顶元素出栈，直到栈为空或者栈顶元素小于当前值为止，其中最后一个出栈的就是当前元素的父节点。我们来看下代码
public boolean verifyPostorder1(int[] postorder) { Stack<Integer> stack = new Stack<>(); int parent = Integer.MAX_VALUE; //注意for循环是倒叙遍历的 for (int i = postorder.length - 1; i >= 0; i--) { int cur = postorder[i]; //当如果前节点小于栈顶元素，说明栈顶元素和当前值构成了倒叙， //说明当前节点是前面某个节点的左子节点，我们要找到他的父节点 while (!stack.isEmpty() && stack.peek() > cur) { parent = stack.pop(); } //只要遇到了某一个左子节点，才会执行上面的代码，才会更 //新parent的值，否则parent就是一个非常大的值，也就 //是说如果一直没有遇到左子节点，那么右子节点可以非常大 if (cur > parent) return false; //入栈 stack.add(cur); } return true; }
上面代码可能大家有点蒙的是if(cur>parent)这一行的判断。二叉搜索树应该是左子节点小于根节点，右子节点大于根节点，但上面为什么大于父节点的时候要返回false，注意这里的parent是在什么情况下赋的值，parent并不一定都是父节点的值，相对于遇到了左子节点的时候他是左子节点的父节点。如果是右子节点，parent就是他的某一个祖先节点，并且这个右子节点是这个祖先节点的一个左子树的一部分，所以不能超过他，有点绕，慢慢体会。
总结：
这题第一种方式是最容易想到的，每次把数组劈两半，因为通过第一个while循环，左边的都是小于根节点的，然后再判断右边的是不是都大于根节点，然后左右两边再以同样的方式计算……。第二种方式也能解决，但比较绕，相对来说不太好容易理解，但如果真的搞懂了，会豁然开朗，也会有很大的收获。
