锦标赛选举算法

 

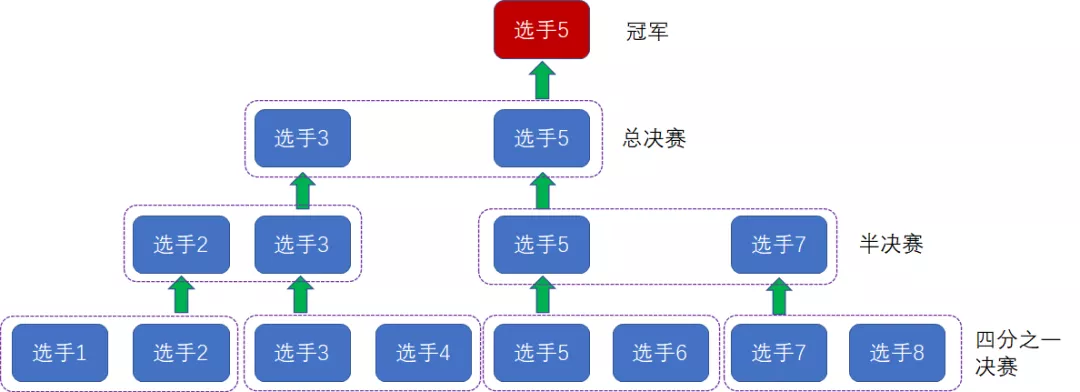
 第二个亚军

 

 只有冠军才能打败亚军，所以亚军一定出现再冠军晋级的路上

 

 

如图中所示，我们把原本的冠军选手5排除掉，在四分之一决赛和他同一组的选手6就自然获得了直接晋级。

 

接下来的半决赛，选手7打败选手6晋级；在总决赛，选手7打败选手3晋级，成为了新的冠军。

 

因此我们可以判断出，选手7是总体上的亚军。

假如给定如下数组，要求从小到大进行升序排列：

 

 第一步，我们根据数组建立一颗满二叉树，用于进行“锦标赛式”的多层次比较。数组元素位于二叉树的叶子结点，元素数量不足时，用空结点补齐。

 

 

 

 

第二步，像锦标赛那样，让相邻结点进行两两比较，把数值较小的结点“晋升“到父结点。

 

 

 

 

 

如此一来，树的根结点一定是值最小的结点，把它复制到原数组的最左侧：

 

 

 

 

第三步，删除原本的最小结点，也就是值为1的结点。然后针对该结点所在路径，进行重新比较和刷新。

 

 

 

如此一来，树的根结点换成了第二小的结点，把

 

 

它复制到原数组的下一个位置：

 

 

 

第四步，删除原本第二小的结点，也就是值为2的结点。然后针对该结点所在路径，进行重新比较和刷新。

 

 

 

如此一来，树的根结点换成了第三小的结点，把它复制到原数组的下一个位置：

 

 

 

像这样不断删除剩余的最小结点，局部刷新二叉树，最终完成了数组的升序排列：

 

public class TournamentSort {

    public static void tournamentSort(int[] array) {
        Node[] tree = buildTree(array);

        for(int i=0; i<array.length; i++){
            array[i] = tree[0].data;
            if(i<array.length-1) {
                //当前最小元素所对应的叶子结点置空
                tree[tree[0].index] = null;
                //重新选举最小元素
                updateTree(tree[0].index, tree);
            }
        }
    }

    //排序前为数组构建二叉树，并选举最小值到树的根结点
    public static Node[] buildTree(int[] array) {
        //计算叶子层的结点数
        int leafSize = nearestPowerOfTwo(array.length);
        //计算二叉树的总结点数
        int treeSize = leafSize * 2 - 1;
        Node[] tree = new Node[treeSize];
        //填充叶子结点
        for(int i=0; i<array.length; i++){
            tree[i+leafSize-1] = new Node(i+leafSize-1, array[i]);
        }
        //自下而上填充非叶子结点
        int levelSize = leafSize;
        int lastIndex = treeSize-1;
        while(levelSize > 1){
            for(int i=0; i<levelSize; i+=2){
                Node right = tree[lastIndex-i];
                Node left = tree[lastIndex-i-1];
                Node parent = left;
                if(left != null && right != null) {
                    parent = left.data<right.data?left:right;
                }else if (left == null){
                    parent = right;
                }
                if(parent != null){
                    int parentIndex = (lastIndex-i-1)/2;
                    tree[parentIndex] = new Node(parent.index, parent.data);
                }
            }
            lastIndex -= levelSize;
            levelSize = levelSize/2;
        }
        return tree;
    }

    //重新选举最小元素
    public static void updateTree(int index, Node[] tree){

        while(index != 0){
            Node node = tree[index];
            Node sibling = null;
            if((index&1) == 1){
                //index为奇数，该结点是左孩子
                sibling = tree[index+1];
            }else {
                //index为偶数，该结点是右孩子
                sibling = tree[index-1];
            }

            Node parent = node;
            int parentIndex = (index-1)/2;
            if(node != null && sibling != null) {
                parent = node.data<sibling.data?node:sibling;
            }else if (node == null){
                parent = sibling;
            }
            tree[parentIndex] = parent==null ? null : new Node(parent.index, parent.data);
            index = parentIndex;
        }
    }

    //获得仅大于number的完全平方数
    public static int nearestPowerOfTwo(int number) {
        int square = 1;
        while(square < number){
            square = square<<1;
        }
        return square;
    }

    //结点类
    private static class Node {
        int data;
        int index;

        Node(int index, int data){
            this.index = index;
            this.data = data;
        }
    }

    public static void main(String[] args) {
        int[] array = {9,3,7,1,5,2,8,10,11,19,4};
        tournamentSort(array);
        System.out.println(Arrays.toString(array));
    }

}