机器学习(二)-信息熵,条件熵,信息增益,信息增益比,基尼系数
一、信息熵的简介
2.1 信息的概念
信息是用来消除随机不确定性的东西。对于机器学习中的决策树而言,如果待分类的事物集合可以划分为多个类别当中,则第k类的信息可以定义如下:
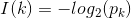
2.2 信息熵概念
信息熵是用来度量不确定性,当熵越大,k的不确定性越大,反之越小。假定当前样本集合D中第k类样本所占的比例为pk (k=1,2,...,|y|),则D的信息熵定义为:
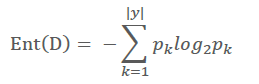
信息增益在决策树算法中是用来选择特征的指标,信息增益越大,则这个特征的选择性越好。同上,计算特征a对样本集D进行划分所获得的信息增益为:
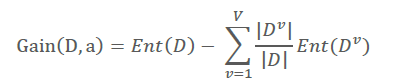
其中:V表示依据特征a对样本集D划分后,获得的总共类别数量;表示每一个新类别中样本数量。
事实上,信息增益准则对可取值数目较多的特征有所偏好,为了减少这种偏好可能带来的不利影响,C4.5决策树算法使用了“增益率”:
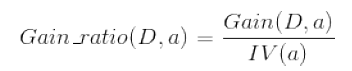
其中IV(a)称为属性a的“固有值”:
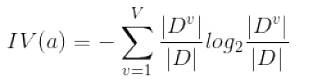
需要注意的是,增益率准则对可取值数目较少的属性所有偏好,因此,C4.5算法并不是直接选择增益率最大的候选划分属性,而是使用了一个启发式:先从候选划分属性中找出信息增益高于平均水平的属性,再从中选择增益率最高的。
2.3 信息熵在决策树中的应用(C4.5算法)
C4.5是决策树算法的一种。决策树算法作为一种分类算法,目标就是将具有p维特征的n个样本分到c个类别中去。相当于做一个投影,c=f(n),将样本经过一种变换赋予一种类别标签。决策树为了达到这一目的,可以把分类的过程表示成一棵树,每次通过选择一个特征来进行分叉。
那么怎样选择分叉的特征呢?每一次分叉选择哪个特征对样本进行划分可以最快最准确的对样本分类呢?不同的决策树算法有着不同的特征选择方案。ID3用信息增益,C4.5用信息增益率,CART用gini系数。
下面以一个例子来直观理解决策树过程。数据集D有四个属性(特征),特征集合A={ 天气,温度,湿度,风速},类别集合L={进行,取消}。

第一步:计算样本集D的信息熵
类别信息熵表示的是所有样本中各种类别出现的不确定性之和。根据熵的概念,熵越大,不确定性就越大,识别类别标签所需要的信息量就越多。
Ent(D) = -9/14*log2(9/14) – 5/14*log2(5/14) = 0.940
第二步:依据每个特征划分样本集D,并计算每个特征(划分样本集D后)的信息熵
Ent(天气) = 5/14*[-2/5*log2(2/5)-3/5*log2(3/5)] + 4/14*[-4/4*log2(4/4)] + 5/14*[-3/5log2(3/5) – 2/5*log2(2/5)] = 0.694
Ent(温度) = 0.911
Ent(湿度) = 0.789
Ent(风速) = 0.892
第三步:计算信息增益
信息增益就是ID3算法的特征选择指标。信息增益的 = 熵 - 条件熵,在这里就是类别信息熵 - 属性信息熵,它表示的是信息不确定性减少的程度。如果一个属性的信息增益越大,就表示用这个属性进行样本划分可以更好的减少划分后样本的不确定性,当然,选择该属性就可以更快更好地完成我们的分类目标。
Gain(天气) = Ent(D) - Ent(天气) = 0.246
Gain(温度) = Ent(D) - Ent(温度) = 0.029
Gain(湿度) = Ent(D) - Ent(湿度) = 0.150
Gain(风速) = Ent(D) - Ent(风速) = 0.048
第四步:计算属性(特征)分裂信息度量
用分裂信息度量来考虑某种属性进行分裂时分支的数量信息和尺寸信息,我们把这些信息称为属性的内在信息(instrisic information)。信息增益率用信息增益 / 内在信息,会导致属性的重要性随着内在信息的增大而减小(即,如果这个属性本身不确定性就很大,那就越不倾向于选取它),这对单纯用信息增益有所补偿。
IV(天气) = -5/14*log2(5/14) – 4/14*log2(4/14) – 5/14*log2(5/14) = 1.577
IV(温度) = 1.556
IV(湿度) = 1.000
IV(风速) = 0.985
第五步:计算信息增益率
Gain_ratio(天气) = 0.246 / 1.577 = 0.155
Gain_ratio(温度) = 0.0187
Gain_ratio(湿度) = 0.151
Gain_ratio(风速) = 0.048
天气的信息增益率最高,选择天气为分裂属性。发现分裂了之后,天气是“阴”的条件下,类别是”纯“的,所以把它定义为叶子节点,选择不“纯”的结点继续分裂。
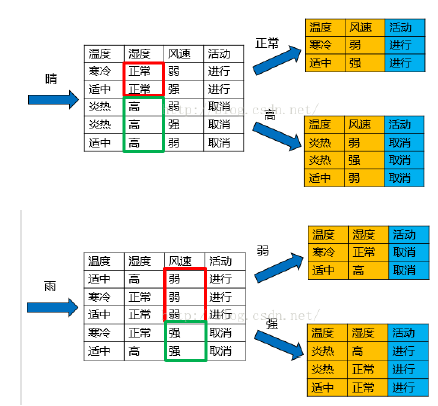
在子结点当中重复过程1~5。至此,这个数据集上C4.5的计算过程就算完成了,一棵树也构建出来了。
总结(C4.5):
While (当前节点“不纯”):
- 计算当前节点的类别熵Ent(D) (以类别取值计算)
- 计算当前节点的属性(特征)熵Ent(pi) (按照属性(特征)取值下的类别取值计算)
- 计算各个属性(特征)的信息增益Gain(pi) = Ent(D) – Ent(pi)
- 计算各个属性(特征)的分类信息度量(内在信息)IV(pi) (按照属性(特征)取值计算)
- 计算各个属性(特征)的信息增益率
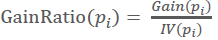
End while
当前节点设置为叶子节点
二、基尼系数概念
我们知道,在ID3算法中我们使用了信息增益来选择特征,信息增益大的优先选择。在C4.5算法中,采用了信息增益比来选择特征,以减少信息增益容易选择特征值多的特征的问题。但是无论是ID3还是C4.5,都是基于信息论的熵模型的,这里面会涉及大量的对数运算。能不能简化模型同时也不至于完全丢失熵模型的优点呢?有!CART分类树算法使用基尼系数来代替信息增益比,基尼系数代表了模型的不纯度,基尼系数越小,则不纯度越低,特征越好。这和信息增益(比)是相反的。
具体的,在分类问题中,假设有K个类别,第k个类别的概率为pk, 则基尼系数的表达式为:
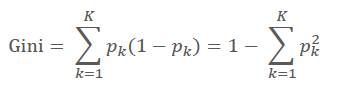
对于个给定的样本D,假设有K个类别,第k个类别的数量为,则样本D的基尼系数表达式为:
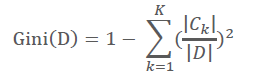
特别的,对于样本D,如果根据特征A的某个值a,把D分成D1和D2两部分,则在特征A的条件下,D的基尼系数表达式为:
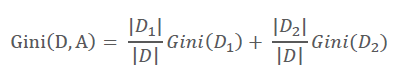
大家可以比较下基尼系数表达式和熵模型的表达式,二次运算是不是比对数简单很多?尤其是二类分类的计算,更加简单。但是简单归简单,和熵模型的度量方式比,基尼系数对应的误差有多大呢?对于二类分类,基尼系数和熵之半的曲线如下:
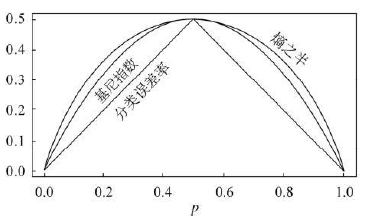
从上图可以看出,基尼系数和熵之半的曲线非常接近,仅仅在45度角附近误差稍大。因此,基尼系数可以做为熵模型的一个近似替代。而CART分类树算法就是使用的基尼系数来选择决策树的特征。同时,为了进一步简化,CART分类树算法每次仅仅对某个特征的值进行二分,而不是多分,这样CART分类树算法建立起来的是二叉树,而不是多叉树。这样一可以进一步简化基尼系数的计算,二可以建立一个更加优雅的二叉树模型。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号