一、EDA分析
EDA分析是做数据建模的第一步,主要是作用是用于熟悉数据,看各个特征的一些数据分布情况。 这里主要使用sns做一些可视化展示数据分布,使用corr,describe,info等熟悉数据特征的情况。
#coding:utf-8 import numpy as np import pandas as pd import seaborn as sns import matplotlib.pyplot as plt from scipy import stats from scipy.stats import norm train = pd.read_csv('train.csv') test = pd.read_csv('test.csv')
# 区分类别型变量(qualitative)和数值型变量(quantiative)
quantitative = [f for f in train.columns if train.dtypes[f] != 'object']
quantitative.remove('SalePrice')
quantitative.remove('Id')
qualitative = [f for f in train.columns if train.dtypes[f] == 'object']
一、整体分析(overview)
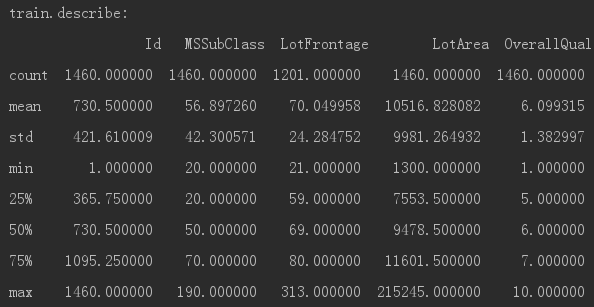
1)使用 describe 进行查看数据特征的count,mean,std,min,四分位数等。
print("train.describe:",'\n',train.describe())
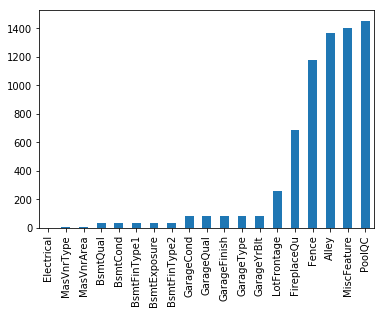
2)查看数据的整体缺失情况,可以使用isnull(),missingno包查看;
missing = train.isnull().sum() missing = missing[missing > 0] missing.sort_values(inplace=True) missing.plot.bar()
使用missingno包(没有包的需要pip install一下包)
import pandas_profiling
pandas_profiling.ProfileReport(train_agg)
能够看到每个特征的缺失值情况,相关性大小,特征类别,偏斜情况等。

msno.matrix(filtered_beh_tgt_mergeA.sample(500), figsize=(16, 7), width_ratios=(15, 1))
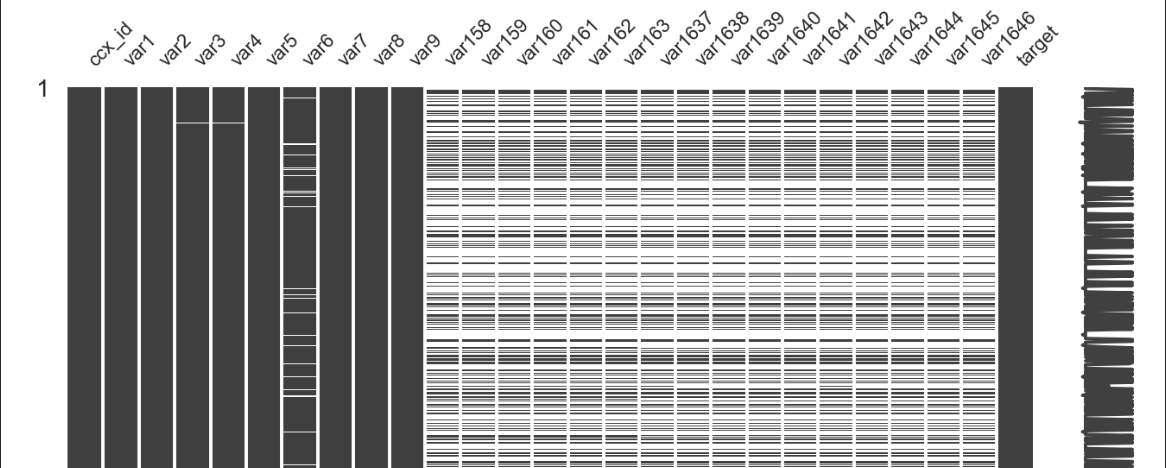
3)数据分布情况 scipy.stats
通用方法
| rvs | 随机变量 |
| 概率密度函 | |
| cdf | 累计分布函数 |
| sf | 残差函数(1-CDF) |
| ppf | 分位点函数(CDF的逆) |
| isf | 逆残存函数(sf的逆) |
| stats | 返回均值,方差,(费舍尔)偏态,(费舍尔)峰度 |
| moment | 分布的非中心距 |
import scipy.stats as st
y = train['SalePrice']
plt.figure(1); plt.title('Johnson SU')
sns.distplot(y, kde=False, fit=st.johnsonsu) # kde核密度估计,kde=true,表示显示核密度估计
plt.figure(2); plt.title('Normal')
sns.distplot(y, kde=True, fit=st.norm)
plt.figure(3); plt.title('Log Normal')
sns.distplot(y, kde=False, fit=st.lognorm)
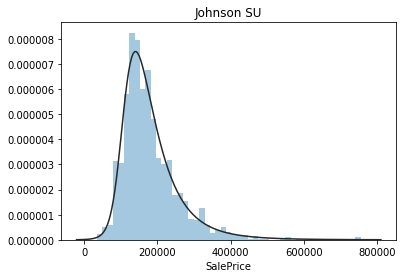

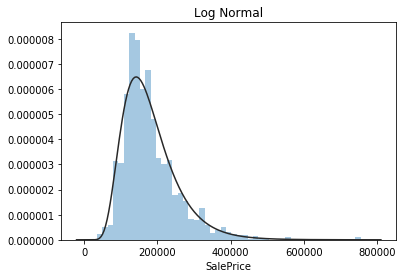
目标值SalePrice不遵循正态分布,根据后续算法需要可以进行相应的转换。 虽然log转换可以解决,但效果最好的是 johnsonsu 分布。
scipy.stats.shapiro shapiro是用来专门做正态性检验的模块,shapiro不合适做样本数 > 5000的正态性检验,检验结果的P值可能不准确
scipy.stats.shapiro(x,a=None,reta=False) x为待检验数据,一般只只使用x就行
>>> from scipy import stats
>>> np.random.seed(12345678)
>>> x = stats.norm.rvs(loc=5, scale=3, size=100)
>>> stats.shapiro(x)
(0.9772805571556091, 0.08144091814756393) # 输出结果的第一个数为统计数,第二个为P值
test_normality = lambda x: stats.shapiro(x.fillna(0))[1] < 0.01
normal = pd.DataFrame(train[quantitative])
normal = normal.apply(test_normality)
print(not normal.any())
>> False # 说明所有的数值型变量分布均不属于正态分布,需要进行数据转换
pandas.melt(frame,id_vars=None,value_vars=None,var_name=‘value’,col_level=None)
frame:要处理的数据集;id_vars:不需要被转换的列名,value_vars需要转换的列名,如果剩下的列全部要转换,就不用写了,
var_name和value_name是自定义设置对应的列名,col_level:如果列是MultiIndex,则使用此级别。
f = pd.melt(train, value_vars=quantitative)
g = sns.FacetGrid(f, col="variable", col_wrap=4, sharex=False, sharey=False)
g = g.map(sns.distplot, "value")

二、相关性(连续型变量)
相关性可以用sns包中heatmap、barplot实现数据之间的相关性;可以使用 sns.pairplot观察成对变量之间的分布情况。
# 相关性协方差表,corr()函数,返回结果接近0说明无相关性,大于0说明是正相关,小于0是负相关.
train_corr = train.drop('Id',axis=1).corr()
print(train_corr)
a = plt.subplots(figsize = (20,12)) #调整画布大小
a=sns.heatmap(train_corr,vmax=.8,square=True) #画热力图 annot = True 显示系数
a.set_yticklabels(a.get_yticklabels(), rotation=360)
a.set_xticklabels(train_corr.index, rotation='vertical')
plt.show()

有时候可能特征比较多,可能我们只需要观察部分特征,比如那些和目标特征相关系数比较大的前10个,可以用如下程序。
#SalePrice 相关度特征排序
# 寻找K个最相关的特征信息
k = 10 #number of varables for heatmap
cols = train_corr.nlargest(k,'SalePrice')['SalePrice'].index
cm = np.corrcoef(train[cols].values.T)
sns.set(font_scale=1.5)
hm = plt.subplots(figsize = (20,12))
hm = sns.heatmap(cm, cmap='RdBu', linewidths=0.05, cbar=True, annot=True, square=True, fmt='.2f', annot_kws={'size': 10}, yticklabels=cols.values, xticklabels=cols.values)
hm.set_yticklabels(hm.get_yticklabels(), rotation=360)
hm.set_xticklabels(train_corr.index, rotation='vertical')
plt.show()

sns.set() #设置主题,调色板等 cols = ['SalePrice','OverallQual','GrLivArea','TotalBsmtSF','FullBath','YearBuilt'] sns.pairplot(train[cols],size=2.0) plt.show() print(train[['SalePrice','OverallQual','GrLivArea','GarageCars','TotalBsmtSF','FullBath','YearBuilt']].info())

def spearman(frame, features): spr = pd.DataFrame() spr['feature'] = features spr['spearman'] = [frame[f].corr(frame['SalePrice'], 'spearman') for f in features] spr = spr.sort_values('spearman') plt.figure(figsize=(6, 0.25*len(features))) sns.barplot(data=spr, y='feature', x='spearman', orient='h') features = quantitative spearman(train, features)
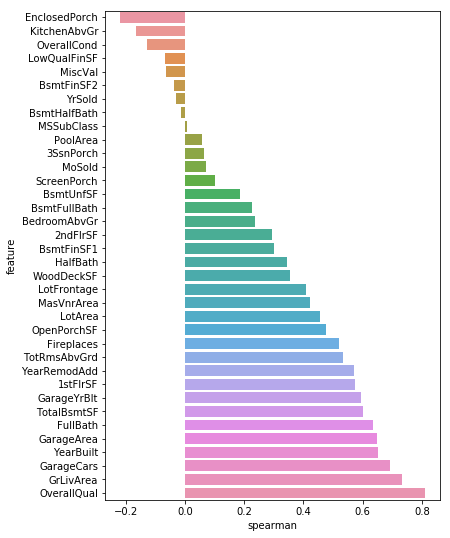
features = quantitative
standard = train[train['SalePrice'] < 200000]
pricey = train[train['SalePrice'] >= 200000]
diff = pd.DataFrame()
diff['feature'] = features
diff['difference'] = [(pricey[f].fillna(0.).mean() - standard[f].fillna(0.).mean())/(standard[f].fillna(0.).mean())
for f in features]
sns.barplot(data=diff, x='feature', y='difference')
x=plt.xticks(rotation=90)

pairplots查看特征与目标之间的变化关系
def pairplot(x, y, **kwargs):
ax = plt.gca()
ts = pd.DataFrame({'time': x, 'val': y})
ts = ts.groupby('time').mean()
ts.plot(ax=ax)
plt.xticks(rotation=90)
f = pd.melt(train, id_vars=['SalePrice'], value_vars=quantitative+qual_encoded)
g = sns.FacetGrid(f, col="variable", col_wrap=2, sharex=False, sharey=False, size=5)
g = g.map(pairplot, "value", "SalePrice")

三、异常值检测
箱线图可以看出数据的集中程度,异常值,平均值等情况,可以将其作为异常值的一种检测手段。
def boxplot(x, y, **kwargs): sns.boxplot(x=x, y=y) x=plt.xticks(rotation=90) f = pd.melt(train, id_vars=['SalePrice'], value_vars=qualitative) g = sns.FacetGrid(f, col="variable", col_wrap=4, sharex=False, sharey=False, size=5) g = g.map(boxplot, "value", "SalePrice")



