卡尔曼滤波
参考:https://www.zhihu.com/question/22422121/answer/22877882
参考:https://blog.csdn.net/coming_is_winter/article/details/79048700
以知乎上给的例子为例(非常通俗易懂):





再给一个例子:
小车在t时刻的状态[pt, vt]如下所示:

其中pt表示小车的位置信息,vt表示小车的速度,ut表示对小车的控制量;
已知小车上一时刻的状态,现在考虑小车t时刻的状态,那么有如下公式:
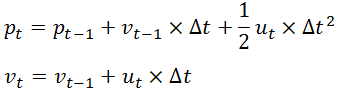
如上式子可以用下面的矩阵来表示该线性关系:
![]()
其中:
![]()
这里就涉及卡尔曼的状态预测公式,其中Ft表示状态转移矩阵,表示如何从上一状态推测当前状态;B是控制矩阵,表示控制量ut如何作用于当前状态;
![]()
其中x变量头上的^表示为估计值x,时刻t上的-表示状态是从上一时刻推测而来;后面通过对其修正得到最优估计,然后再去除- ;
由于是对真实值进行估计,那么就存在噪声的影响,假设噪声服从0均值高斯分布,即Noise~Guassian(0,σ);若要对某维度数据进行估计,则加入噪声的影响,那么只考虑其方差σ即可;
当维度增加,为了考虑多个维度噪声的影响,则引入噪声协方差矩阵Σ;
由于系统中每一时刻的不确定性都是通过协方差矩阵Σ来给定,且该不确定性会随着时间而传递,这种不确定性的传递通过状态转移矩阵来表示:
![]()
同时考虑到由于模型本身也不一定正确,所以通过协方差矩阵Q来预测模型本身的噪声(噪声的不确定性的传递):
![]()
这也是卡尔曼中第二条公式,表示不确定性传递的过程;


 浙公网安备 33010602011771号
浙公网安备 33010602011771号