特征筛选(随机森林)
参考:http://blog.csdn.net/zjuPeco/article/details/77371645?locationNum=7&fps=1
一般情况下,数据集的特征成百上千,因此有必要从中选取对结果影响较大的特征来进行进一步建模,相关的方法有:主成分分析、lasso等,这里我们介绍的是通过随机森林来进行筛选。
用随机森林进行特征重要性评估的思想比较简单,主要是看每个特征在随机森林中的每棵树上做了多大的贡献,然后取平均值,最后比较不同特征之间的贡献大小。
贡献度的衡量指标包括:基尼指数(gini)、袋外数据(OOB)错误率作为评价指标来衡量。
衍生知识点:权重随机森林的应用(用于增加小样本的识别概率,从而提高总体的分类准确率)
随机森林/CART树在使用时一般通过gini值作为切分节点的标准,而在加权随机森林(WRF)中,权重的本质是赋给小类较大的权重,给大类较小的权重。也就是给小类更大的惩罚。权重的作用有2个,第1点是用于切分点选择中加权计算gini值,表达式如下:
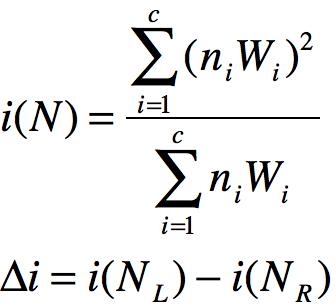
其中,N表示未分离的节点,NL和NR分别表示分离后的左侧节点和右侧节点,Wi为c类样本的类权重,ni表示节点内各类样本的数量,Δi是不纯度减少量,该值越大表明分离点的分离效果越好。
第2点是在终节点,类权重用来决定其类标签,表达式如下:
![]()
参考文献:随机森林针对小样本数据类权重设置 https://wenku.baidu.com/view/07ba98cca0c7aa00b52acfc789eb172ded639998.html
这里介绍通过gini值来进行评价,我们将变量的重要性评分用VIM来表示,gini值用GI表示,假设有m个特征X1,X2,...Xc,现在要计算出每个特征Xj的gini指数评分VIMj,即第j个特征在随机森林所有决策树中节点分裂不纯度的平均改变量,gini指数的计算公式如下表示:
![]()
其中,k表示有k个类别,pmk表示节点m(将特征m逐个对节点计算gini值变化量)中类别k所占的比例。
特征Xj在节点m的重要性,即节点m分枝前后的gini指数变化量为:
![]()
其中GIl和GIr分别表示分枝后两个新节点的gini指数。
如果特征Xj在决策树i中出现的节点在集合M中,那么Xj在第i棵树的重要性为:
![]()
假设随机森林共有n棵树,那么:
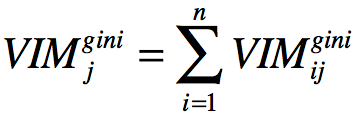
最后把所有求得的重要性评分进行归一化处理就得到重要性的评分:

通过sklearn中的随机森林返回特征的重要性:
from sklearn.ensemble import RandomForestClassifier forest = RandomForestClassifier(n_estimators=10000, random_state=0, n_jobs=-1) importances = forest.feature_importances_ #样例的输出结果如下所示 1) Alcohol 0.182483 2) Malic acid 0.158610 3) Ash 0.150948 4) Alcalinity of ash 0.131987 5) Magnesium 0.106589 6) Total phenols 0.078243 7) Flavanoids 0.060718 8) Nonflavanoid phenols 0.032033 9) Proanthocyanins 0.025400 10) Color intensity 0.022351 11) Hue 0.022078 12) OD280/OD315 of diluted wines 0.014645 13) Proline 0.013916
举个样例:
from sklearn.datasets import load_iris from sklearn.ensemble import RandomForestClassifier import pandas as pd import numpy as np iris = load_iris() df = pd.DataFrame(iris.data, columns=iris.feature_names) df['is_train'] = np.random.uniform(0, 1, len(df)) <= .75 df['species'] = pd.Categorical.from_codes(iris.target, iris.target_names) df.head() train, test = df[df['is_train']==True], df[df['is_train']==False] features = df.columns[:4] clf = RandomForestClassifier(n_jobs=2) y, _ = pd.factorize(train['species']) clf.fit(train[features], y) preds = iris.target_names[clf.predict(test[features])] pd.crosstab(test['species'], preds, rownames=['actual'], colnames=['preds']) clf.feature_importances_
#返回特征重要性的结果:
[ 0.085598 , 0.01877088, 0.45324092, 0.4423902 ]
sklearn.metrics中的评估方法介绍:
1、sklearn.metrics.roc_curve(true_y. pred_proba_score, pos_labal) #返回roc曲线的3个属性:fpr, tpr,和阈值 import numpy as np from sklearn.metrics import roc_curve y = np.array([1,1,2,2]) pred = np.array([0.1, 0.4, 0.35, 0.8]) fpr, tpr, thresholds = roc_curve(y, pred, pos_label=2) fpr # array([ 0. , 0.5, 0.5, 1. ]) tpr # array([ 0.5, 0.5, 1. , 1. ]) thresholds #array([ 0.8 , 0.4 , 0.35, 0.1 ]) from sklearn.metrics import auc metrics.auc(fpr, tpr) 2、sklearn.metrics.auc(x, y, reorder=False) #计算AUC值,其中x,y分别为数组形式,根据(xi,yi)在坐标上的点,生成的曲线,计算AUC值 3、sklearn.metrics.roc_auc_score(true_y, pred_proba_y) #直接根据真实值(必须是二值)、预测值(可以是0/1,或是prob)计算出auc值
参考:http://blog.csdn.net/cherdw/article/details/54971771
网格搜索调参:
grid.fit():运行网格搜索
grid_scores_:给出不同参数情况下的评价结果
best_params_:描述了已取得最佳结果的参数的组合
best_score_:成员提供优化过程期间观察到的最好的评分
param_test1= {'n_estimators':range(10,71,10)} #对参数'n_estimators'进行网格调参
gsearch1= GridSearchCV(estimator = RandomForestClassifier(min_samples_split=100,min_samples_leaf=20,max_depth=8,max_features='sqrt' ,random_state=10), param_grid =param_test1, scoring='roc_auc',cv=5)
gsearch1.fit(X,y)
gsearch1.grid_scores_,gsearch1.best_params_, gsearch1.best_score_ #输出调参结果,并返回最优下的参数
#输出结果如下:
([mean:0.80681, std: 0.02236, params: {'n_estimators': 10},
mean: 0.81600, std: 0.03275, params:{'n_estimators': 20},
mean: 0.81818, std: 0.03136, params:{'n_estimators': 30},
mean: 0.81838, std: 0.03118, params:{'n_estimators': 40},
mean: 0.82034, std: 0.03001, params:{'n_estimators': 50},
mean: 0.82113, std: 0.02966, params:{'n_estimators': 60},
mean: 0.81992, std: 0.02836, params:{'n_estimators': 70}],
{'n_estimators':60}, 0.8211334476626017)
#多个特征的网格搜索,如下所示
param_test2= {'max_depth':range(3,14,2),'min_samples_split':range(50,201,20)}
gsearch2= GridSearchCV(estimator = RandomForestClassifier(n_estimators= 60, min_samples_leaf=20,max_features='sqrt' ,oob_score=True,random_state=10), param_grid = param_test2,scoring='roc_auc',iid=False, cv=5)
gsearch2.fit(X,y)
gsearch2.grid_scores_,gsearch2.best_params_, gsearch2.best_score_
#通过查看袋外准确率(oob)来判别参数调整前后准确率的变化情况
rf1= RandomForestClassifier(n_estimators= 60, max_depth=13, min_samples_split=110, min_samples_leaf=20,max_features='sqrt' ,oob_score=True,random_state=10)
rf1.fit(X,y)
print(rf1.oob_score_)
#通过每次对1-3个特征进行网格搜索,重复此过程直到遍历每个特征,并得到最终的调参结果。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号