奇异值分解(SVD)(基础知识)
参考:https://www.cnblogs.com/pinard/p/6251584.html
参考:http://blog.csdn.net/u010099080/article/details/68060274
参考:https://www.zhihu.com/question/22237507
定义:
SVD用于对矩阵进行分解,假设待分解矩阵A大小为m×n的矩阵,那么矩阵A的SVD为:
![]()
以上的U是一个mxm的矩阵,Σ是一个mxn的矩阵,除了主对角线意外其他值均为0,主对角线上每个元素均为奇异值,V是一个nxn的矩阵,且U和V均满足![]() .
.
下面则介绍如何求得U、Σ、V的过程。
我们将A的转置和A作矩阵相乘,那么得到nxn的方阵![]() ,由于这是一个方阵,那么我们可以进行特征分解,得到特征值和特征向量满足下式子:
,由于这是一个方阵,那么我们可以进行特征分解,得到特征值和特征向量满足下式子:
![]()
这样我们则得到![]() 的特征值和对应的特征向量,将特征向量组成一个nxn的矩阵,那么就得到SVD公式的V矩阵,一般将V的每个特征向量叫做A的右奇异向量。
的特征值和对应的特征向量,将特征向量组成一个nxn的矩阵,那么就得到SVD公式的V矩阵,一般将V的每个特征向量叫做A的右奇异向量。
若将A和A的转置作矩阵相乘,那么得到mxm的矩阵![]() ,同样进行特征分解,得到如下的特征值和特征向量:
,同样进行特征分解,得到如下的特征值和特征向量:
![]()
这样则得到对应的m个特征向量u和m个特征值,将![]() 的所有特征向量组成一个mxm的特征矩阵U,那么就能得到SVD矩阵里的U矩阵,一般我们将U中的每个特征向量称为A的左奇异向量。
的所有特征向量组成一个mxm的特征矩阵U,那么就能得到SVD矩阵里的U矩阵,一般我们将U中的每个特征向量称为A的左奇异向量。
剩下的求奇异值矩阵Σ过程,由于其除了对角线上的奇异值之外其他都是0,那么我们只需要求出对应的奇异值σ即可。
由于:
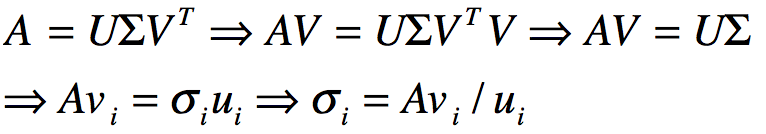
那么我们就可以得到各奇异值,进而得到奇异矩阵Σ.
判断![]() 和
和![]() 得到的特征向量组成的矩阵分别为V矩阵和U矩阵,以如下为例(ΣT=Σ):
得到的特征向量组成的矩阵分别为V矩阵和U矩阵,以如下为例(ΣT=Σ):
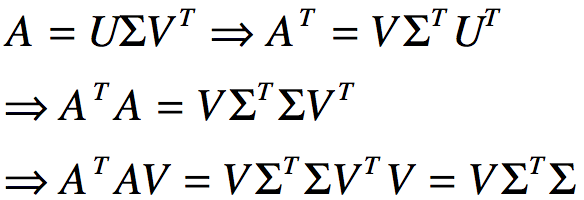
从而发现![]() 的特征向量组成的就是SVD分解中的V矩阵,进一步可以发现特征值矩阵为奇异值矩阵的平方,即得到奇异值和特征值满足关系
的特征向量组成的就是SVD分解中的V矩阵,进一步可以发现特征值矩阵为奇异值矩阵的平方,即得到奇异值和特征值满足关系![]() ,同理可以得到
,同理可以得到![]() 的特征向量组成的就是SVD分解中的U矩阵。
的特征向量组成的就是SVD分解中的U矩阵。
由于奇异值和我们特征分解中的特征值类似,在奇异值矩阵中同样是从大到小排序,且奇异值减小速度非常快,在很多情况下,少量的奇异值之和能占全部奇异值之和的较高的比例,因而我们用最大的k个奇异值及对应的左右奇异向量来近似描述矩阵,即有如下表示:
![]()
其中k比n小很多,即大的矩阵A可以分解为3个小的矩阵来表示。
由于如上性质,SVD分解可以用于PCA降维,可以用来数据压缩和降噪,也可以用于推荐算法,将用户和喜好对应的矩阵作特征分解,进而得到隐含的用户需求来做推荐。
SVD在PCA中的应用:
具体可以参考:https://www.cnblogs.com/pinard/p/6251584.html 中对PCA的讲解
在PCA原理中,提到PCA降维,需要找到样本协方差矩阵![]() 中最大的d个特征向量,然后将这d个最大的特征向量组成矩阵来作低维投影降维,在这个过程中需要先求出协方差矩阵
中最大的d个特征向量,然后将这d个最大的特征向量组成矩阵来作低维投影降维,在这个过程中需要先求出协方差矩阵![]() ,当样本数和特征数都很多的时候计算量会比较大。
,当样本数和特征数都很多的时候计算量会比较大。
由于有些SVD的实现算法可以不先求出对应的协方差矩阵![]() ,也可以得到对应的右奇异矩阵V,即我们不需要对PCA算法做特征分解,而是通过做SVD来完成,该方法在样本量较大的时候比较有效,其中scikit-learn的PCA算法背后真正实现的是SVD算法。
,也可以得到对应的右奇异矩阵V,即我们不需要对PCA算法做特征分解,而是通过做SVD来完成,该方法在样本量较大的时候比较有效,其中scikit-learn的PCA算法背后真正实现的是SVD算法。
另一方面,PCA仅使用了SVD的右奇异矩阵,并没有使用左奇异矩阵。那么左奇异矩阵的作用在于:
假设我们的样本是m x n 的矩阵X,我们通过SVD分解得到![]() 最大的d个特征向量组成的m x d维矩阵U,那么我们通过如下处理:
最大的d个特征向量组成的m x d维矩阵U,那么我们通过如下处理:
![]()
可以得到d x n的矩阵X‘,这个矩阵和我们原来m x n维的样本矩阵X相比,行数从原来的m减少到了d,从而对行数进行压缩,也就是说左奇异矩阵用于对行数压缩,右奇异矩阵用于对列数进行压缩,也就是PCA降维。
例子:
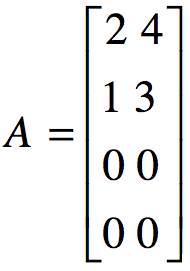 计算得:
计算得:
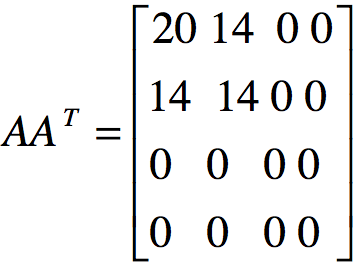
根据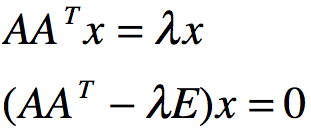 ,得到特征值
,得到特征值![]()
从而得到单位化的特征矩阵U为:
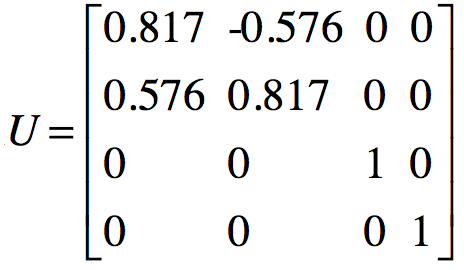
同理求解![]() 的特征值和特征向量,将特征值降序排列之后得到单位化的特征向量矩阵V为:
的特征值和特征向量,将特征值降序排列之后得到单位化的特征向量矩阵V为:
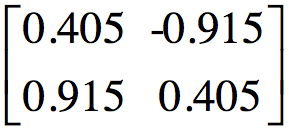
根据特征值的平方根得到对角矩阵:
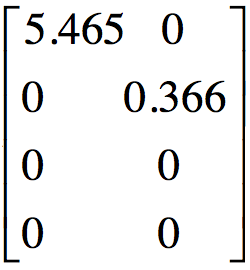
到此,矩阵A通过SVD分解得到:
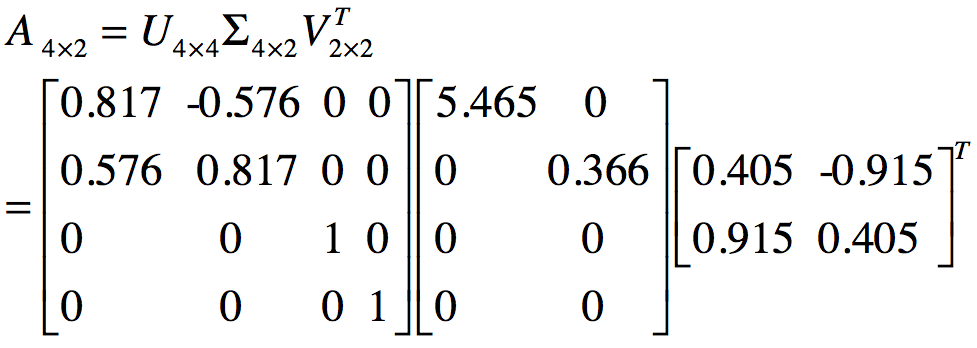


 浙公网安备 33010602011771号
浙公网安备 33010602011771号